So far we have described the magnitude of the magnetic force on a moving electric charge, but not the direction. The magnetic field is
a vector field, thus the force applied will be oriented in a particular direction. There is a clever way to determine this direction using nothing more than your right hand. The direction of the magnetic force $F$ is perpendicular to the plane formed by $v$ and $B$, as determined by the right-hand palm rule, which is illustrated in the figure. The right-hand rule states that to determine the direction of the magnetic force on a positive moving charge, $f$, point the thumb of the right hand in the direction of $v,$ the fingers in the direction of $B,$ and a perpendicular to the palm points in the direction of $F$
Rate of change of B with respect to x is different at different values of x
for $x<\pm \frac{a}{2}$ curve is convex and $\quad$ for $x>\pm \frac{a}{2}$ curve is concave
At $x=\pm \frac{a}{2} \quad$ we get $\frac{d B}{d x}=$ const $,$ and $\frac{d^{2} B}{d x^{2}}=0$
So at $x=+\frac{a}{2} \&-\frac{a}{2}$ B varies linearly with $x$
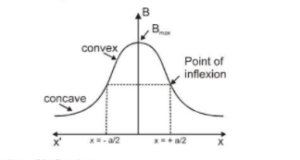These points are called points of inflexion.
Distance in between these two points is equal to radius of the coil
$B=\frac{B_{C}}{\left(1+\frac{x^{2}}{a^{2}}\right)^{3 / 2}}$
$\because$ Magnetic field at the centre of coil $\mathrm{B}_{\mathrm{C}}=\frac{\mu_{0} \mathrm{NI}}{2 \mathrm{a}}$
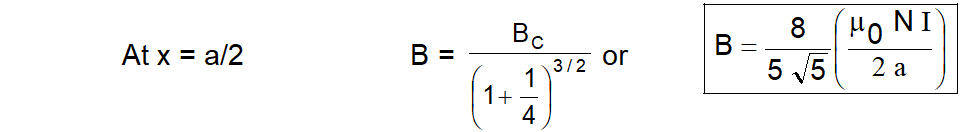
Click here for the Video tutorials of Magnetic Effect of Current Class 12
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.
For free video lectures and complete study material, Download eSaral APP.
a vector field, thus the force applied will be oriented in a particular direction. There is a clever way to determine this direction using nothing more than your right hand. The direction of the magnetic force $F$ is perpendicular to the plane formed by $v$ and $B$, as determined by the right-hand palm rule, which is illustrated in the figure. The right-hand rule states that to determine the direction of the magnetic force on a positive moving charge, $f$, point the thumb of the right hand in the direction of $v,$ the fingers in the direction of $B,$ and a perpendicular to the palm points in the direction of $F$
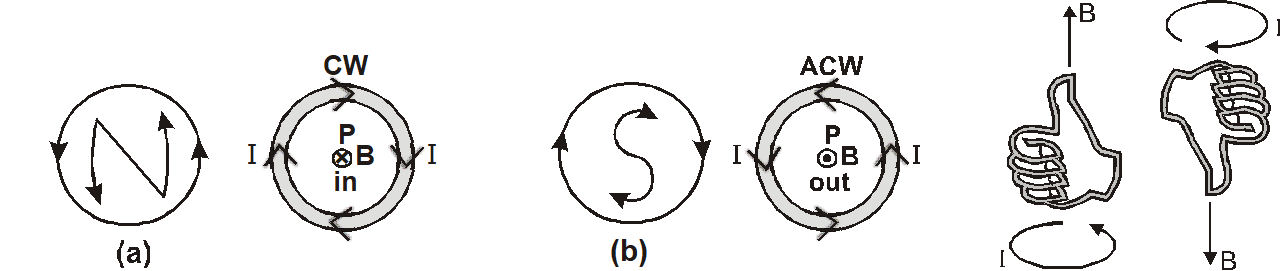
Right Hand Palm Rule
If we hold the thumb of the right hand mutually perpendicular to the grip of the fingers such that the curvature of the finger represents the direction of current in the wire loop, then the thumb of the right hand will point in the direction of the magnetic field near the center of the current loop
Graph of B v/s X
As soon as x increases magnetic field B decreases, dependence of B on x is shown in figureRate of change of B with respect to x is different at different values of x
for $x<\pm \frac{a}{2}$ curve is convex and $\quad$ for $x>\pm \frac{a}{2}$ curve is concave
At $x=\pm \frac{a}{2} \quad$ we get $\frac{d B}{d x}=$ const $,$ and $\frac{d^{2} B}{d x^{2}}=0$
So at $x=+\frac{a}{2} \&-\frac{a}{2}$ B varies linearly with $x$
These points are called points of inflexion.
Distance in between these two points is equal to radius of the coil
$B=\frac{B_{C}}{\left(1+\frac{x^{2}}{a^{2}}\right)^{3 / 2}}$
$\because$ Magnetic field at the centre of coil $\mathrm{B}_{\mathrm{C}}=\frac{\mu_{0} \mathrm{NI}}{2 \mathrm{a}}$
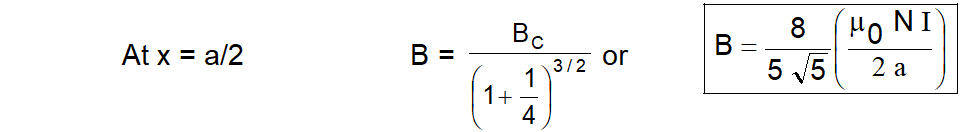
Also Read:
Biot Savart's LawClick here for the Video tutorials of Magnetic Effect of Current Class 12
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.
For free video lectures and complete study material, Download eSaral APP.