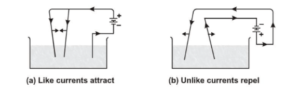
It is an experimentally established fact that two current-carrying conductors attract each other when the current is in the same direction and repel each other when the currents are in opposite direction. Here we will study about Force Between Two Parallel Current Carrying Conductors as wire:
$B_{1}=\frac{\mu_{0} I_{1}}{2 \pi d}$ .......(i)
The field due to the portions of the wire $W_{2},$ above and below $d \ell,$ is zero. Thus, eq" (i) gives
the net field at $\mathrm{d} \ell$ . The direction of this field is perpendicular to the plane of the diagram and going into it. The magnetic force at the element $d \ell$ due to wire $w_{1}$ is.
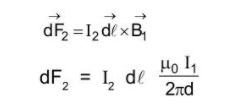The vector product $\overrightarrow{\mathrm{d}} \ell \times \overrightarrow{\mathrm{B}}$ has a direction towards the wire $\mathrm{W}_{1} .$ Thus, the length $\mathrm{d} \ell$ of wire $\mathrm{W}_{2}$ is attracted towards the wire $\mathrm{W}_{1}$. The force per unit length of the wire $\mathrm{W}_{2}$ due to the wire $W_{1}$ is
If we take an element $\mathrm{d} \ell$ in the wire $\mathrm{W}_{1}$ and calculate the magnetic force per unit length on wire $W_{1}$ due to $\mathrm{W}_{2},$ it is again given by $\operatorname{eq}^{n}(i i)$
If the parallel wires currents in opposite directions, the wires repel each other.
The wires attract each other if the current in the wires is flowing in the same direction.
And they repel each other if the currents are in opposite directions.
$\because \quad \mathrm{F}=\frac{\mu_{0}}{2 \pi} \frac{\mathrm{I}_{1} \mathrm{I}_{2}}{\mathrm{r}} \mathrm{N} / \mathrm{m}$
When $\mathrm{I}_{1}=\mathrm{I}_{2}=1$ ampere and $\mathrm{r}=1 \mathrm{m},$ then $\quad \mathrm{F}=\frac{\mu_{0}}{2 \pi}=\frac{4 \pi \times 10^{-7}}{2 \pi} \mathrm{N} / \mathrm{m}=2 \times 10^{-7} \mathrm{N} / \mathrm{m}$ This leads to the following definition of ampere.
One ampere is that current which, if passed in each of two parallel conductors of infinite length and one metre apart in vacuum causes each conductor to experience a force of $2 \times 10^{-7}$ newton per metre of length of conductor.
Dimensional of formula of $\mu_{0}$
$\because \quad \mathrm{F}=\frac{\mu_{0}}{2 \pi} \frac{\mathrm{I}_{1} \mathrm{I}_{2}}{\mathrm{r}} \quad$ so
$\left[\mu_{0}\right]=\frac{[\mathrm{F}][\mathrm{r}]}{\left[\mathrm{I}_{1} \mathrm{I}_{2}\right]}=\frac{\left[\mathrm{ML}^{0} \mathrm{T}^{-2}\right][\mathrm{L}]}{\left[\mathrm{I}^{2}\right]}=\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right]$
Also Read: Biot Savart's Law
Click here for the Video tutorials of Magnetic Effect of Current Class 12
Force Between Parallel Current-Carrying Wires
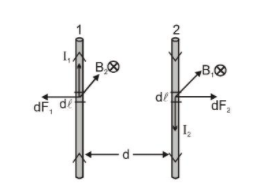
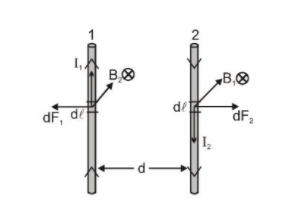
Consider two long wires $W_{1}$ and $W_{2}$ kept parallel to each other and carrying currents $I_{1}$ and $\mathrm{I}_{2}$ respectively in the same direction. The separation between the wires is d. Consider a small element d\ell of the wire $WA_{2}$ The magnetic field at d\ell due to the wire $W_{1}$ is$B_{1}=\frac{\mu_{0} I_{1}}{2 \pi d}$ .......(i)
The field due to the portions of the wire $W_{2},$ above and below $d \ell,$ is zero. Thus, eq" (i) gives
the net field at $\mathrm{d} \ell$ . The direction of this field is perpendicular to the plane of the diagram and going into it. The magnetic force at the element $d \ell$ due to wire $w_{1}$ is.
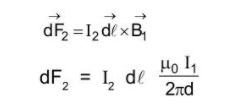The vector product $\overrightarrow{\mathrm{d}} \ell \times \overrightarrow{\mathrm{B}}$ has a direction towards the wire $\mathrm{W}_{1} .$ Thus, the length $\mathrm{d} \ell$ of wire $\mathrm{W}_{2}$ is attracted towards the wire $\mathrm{W}_{1}$. The force per unit length of the wire $\mathrm{W}_{2}$ due to the wire $W_{1}$ is
If we take an element $\mathrm{d} \ell$ in the wire $\mathrm{W}_{1}$ and calculate the magnetic force per unit length on wire $W_{1}$ due to $\mathrm{W}_{2},$ it is again given by $\operatorname{eq}^{n}(i i)$
If the parallel wires currents in opposite directions, the wires repel each other.
The wires attract each other if the current in the wires is flowing in the same direction.
And they repel each other if the currents are in opposite directions.
Experimental Demonstration
Definition of Ampere
$\because \quad \mathrm{F}=\frac{\mu_{0}}{2 \pi} \frac{\mathrm{I}_{1} \mathrm{I}_{2}}{\mathrm{r}} \mathrm{N} / \mathrm{m}$
When $\mathrm{I}_{1}=\mathrm{I}_{2}=1$ ampere and $\mathrm{r}=1 \mathrm{m},$ then $\quad \mathrm{F}=\frac{\mu_{0}}{2 \pi}=\frac{4 \pi \times 10^{-7}}{2 \pi} \mathrm{N} / \mathrm{m}=2 \times 10^{-7} \mathrm{N} / \mathrm{m}$ This leads to the following definition of ampere.
One ampere is that current which, if passed in each of two parallel conductors of infinite length and one metre apart in vacuum causes each conductor to experience a force of $2 \times 10^{-7}$ newton per metre of length of conductor.
Dimensional of formula of $\mu_{0}$
$\because \quad \mathrm{F}=\frac{\mu_{0}}{2 \pi} \frac{\mathrm{I}_{1} \mathrm{I}_{2}}{\mathrm{r}} \quad$ so
$\left[\mu_{0}\right]=\frac{[\mathrm{F}][\mathrm{r}]}{\left[\mathrm{I}_{1} \mathrm{I}_{2}\right]}=\frac{\left[\mathrm{ML}^{0} \mathrm{T}^{-2}\right][\mathrm{L}]}{\left[\mathrm{I}^{2}\right]}=\left[\mathrm{MLT}^{-2} \mathrm{I}^{-2}\right]$
Also Read: Biot Savart's Law
Click here for the Video tutorials of Magnetic Effect of Current Class 12
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.For free video lectures and complete study material, Download eSaral APP.