1. Force on a Charged Particle in a Magnetic Field
2. Difference in Force on a Charged Particle by Magnetic Field and Electric Field

When a charged particle travels through a magnetic field, it experiences a force unlike any other that we’re familiar with in everyday life. To illustrate the point, envision yourself walking down the sidewalk, when all of a sudden, a strong gust of wind hits you from the side. Now imagine that instead of moving sideways, you shoot straight up to the sky. Here we will study about the Force on a Moving Charge in a Magnetic Field.

Force on a Charged Particle in a Magnetic Field

Force experienced by a current element Id $\vec{\ell}$ in magnetic field $\overrightarrow{\mathrm{B}}$ is given by

$\mathrm{dF}=1 \mathrm{~d} \vec{\ell} \times \overrightarrow{\mathrm{B}}$ ………(1)

Now if the current element $\mathrm{Id} \vec{\ell}$ is due to the motion of charge particles, each particle having a charge q moving with velocity $\overrightarrow{\mathrm{v}}$ through a cross-section S,

$\mathrm{Id} \vec{\ell}=\mathrm{n} \mathrm{S} \mathrm{q} \quad \overrightarrow{\mathrm{v}} \cdot \mathrm{d} \ell=\mathrm{n} \mathrm{d} \tau \mathrm{q} \overrightarrow{\mathrm{v}}$ [with volume $\mathrm{d} \tau=\mathrm{S} \mathrm{d} \ell]$

From eq $^{n}$ (i) we can write $\mathrm{dF}=\mathrm{n} \mathrm{d} \tau \mathrm{q}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})$

$n \mathrm{d} \tau=$ the total number of charged particles in volume d\tau $(n=$ number of charged particles per unit volume),

force on a charged particle From this it is clear that : $\left.\vec{F}=\frac{1}{n} \frac{d \vec{F}}{d \tau}=q \quad \vec{v} \times \vec{B}\right)$

(a) The force $\overrightarrow{\mathrm{F}}$ is always perpendicular to both the velocity $\overrightarrow{\mathrm{v}}$ and the field $\overrightarrow{\mathrm{B}}$.

(b) A charged particle at rest in a steady magnetic field does not experience any force.

If the charged particle is at rest then $\overrightarrow{\mathrm{v}}=0,$ so $\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}}=0$

(c) A moving charged particle does not experience any force in a magnetic field if its motion is parallel or antiparallel to the field.

i.e., if $\quad \theta=0^{\circ}$ or $180^{\circ}$



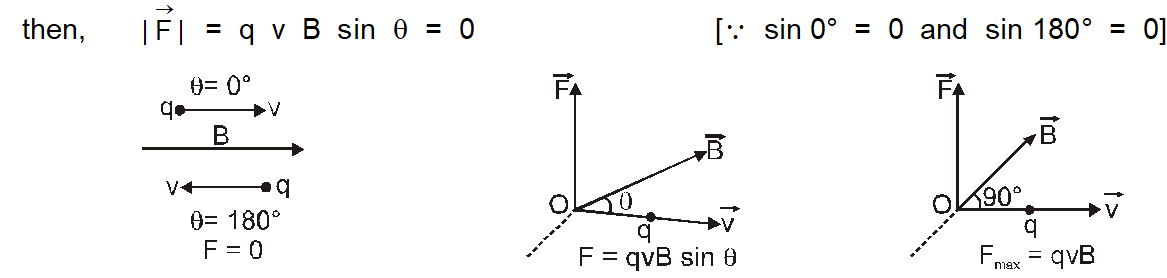
(d) If the particle is moving perpendicular to the field.

In this situation all the three vectors $\overrightarrow{\mathrm{F}}, \overrightarrow{\mathrm{v}}$ and $\overrightarrow{\mathrm{B}}$ are mutually perpendicular to each other. Then $\sin \theta=\max =1,$ i.e., $\theta=90^{\circ}$

The force will be maximum $F_{\max }=q \vee B$

(e) Work done by force due to magnetic field in motion of a charged particle is always zero.

When a charged particle move in a magnetic field, then force acts on it is always perpendicular to displacement,

so the work done, $\left.\quad \mathrm{W}=\int \overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{ds}}=\int \mathrm{F} d \mathrm{s} \cos 90^{\circ}=0 \quad \text { (as } \theta=90^{\circ}\right)$

And as by work-energy theorem $\mathrm{W}=\Delta \mathrm{KE},$ the kinetic energy $\left(=\frac{1}{2} \mathrm{mv}^{2}\right)$, remains unchanged and hence speed of charged particle v remains constant.

However, in this situation the force changes the direction of motion, so the direction of velocity of $\vec{v}$ the charged particle changes continuously.

(f) For motion of charged particle in a magnetic field $\overrightarrow{\mathrm{F}}=\mathrm{q}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})$

So magnetic induction $\overrightarrow{\mathrm{B}}$ can be defined as a vector having the direction in which a moving charged particle does not experience any force in the field and magnitude equal to the ratio of the magnitude of maximum force to the product of the magnitude of charge with velocity

Difference in Force on a Charged Particle by Magnetic Field and Electric Field

Also Read: Biot Savart’s Law

Click here for the Video tutorials of Magnetic Effect of Current Class 12

About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.

For free video lectures and complete study material, Download eSaral APP.