Get states of matter class 11 important questions and answers for various exams.View the Important Question bank for Class 11 Chemistry and other subjects too. These important questions will play significant role in clearing concepts of Chemistry. These questions and answers are designed, keeping States of matter Class 11 syllabus as per NCERT in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions for class 11 chemistry.
Learn the concepts of States of matter and other topics of class 11 with these questions and answers.
Click Here for Detailed Chapter-wise Notes of Chemistry for Class 11th, JEE & NEET.
You can access free study material for all three subject’s Physics, Chemistry and Mathematics.
Click Here for Detailed Notes of any chapter.
eSaral provides you complete edge to prepare for Board and Competitive Exams like JEE, NEET, BITSAT, etc.
We have transformed classroom in such a way that a student can study anytime anywhere. With the help of AI we have made the learning Personalized, adaptive and accessible for each and every one.
Visit eSaral Website to download or view free study material for JEE & NEET.
Also get to know about the strategies to Crack Exam in limited time period.
Q. What is triple point of a substance ?
Ans. It is the point at which solid, liquid and vapour of a substance are in equilibrium with each other. For example, triple point of water is the temperature at which ice, water and its vapour coexist.
Q. $H C l$ is gas while $H F$ is liquid at room temperature, why?
Ans. HF molecules are associated with intermolecular $H-$ bonding, therefore, it is liquid whereas $H C l$ is gas because less Vander Waal's forces of attraction.
Q. What is boiling point of water at (i) higher altitudes, (ii) in pressure cooker?
Ans. $(i)<100^{\circ} C(\text { ii })>100^{\circ} C$
Q. Why is air denser at lower level than at higher altitudes ?
Ans. Heavier air will come down and lighter air goes up. Air at lower level is denser since it is compressed by mass of air above it.
Q. What is dry ice ? Why is it so called ?
Ans. Solid $\mathrm{CO}_{2}$ It is because solid $\mathrm{CO}_{2}$ is directly converted into gaseous state (sublimes) and does not change into liquid, so it is called dry ice.
Q. A rubber balloon permeable to hydrogen in all its isotopic forms is filled with deuterium $\left(D_{2}\right)$ and then placed in a box containing pure hydrogen. Will the balloon expand or contract or remains as it is?
Ans. Balloon will expand because rate of diffusion of $H_{2}$ is greater than that of $D_{2}$
Q. What type of graph would you get when $P V$ is plotted against $P$ at constant temperature?
Ans. A straight line parallel to pressure axis.
Q. Name and state the law governing the expansion of gases when they are heated or cooled at constant pressure.
Ans. Charle’s Law.
Q. At a certain altitude, the density of air is $1 / 10$ th of the density of the earth's atmosphere and temperature is $-10^{\circ} \mathrm{C} .$ What is the pressure at that altitude? Assume that air behaves like an ideal gas, has uniform composition and is at S.T.T. at the earth's surface.
Ans. $\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}$ or $P_{2}=\frac{P_{1} V_{1} T_{2}}{T_{1} V_{2}}$
But $d \propto \frac{1}{V} .$ Hence $P_{2}=\frac{P_{1} T_{2}}{T_{1}}\left(\frac{d_{2}}{d_{1}}\right)$
$=\frac{760 \times 263}{273}\left(\frac{1}{10}\right)=73.2 \mathrm{mm}$
Q. How much time it would take to distribute one Avogadro's number of wheat grains, if $10^{10}$ grains are distributed each second?
[NCERT]
Ans. Number of years $=\frac{6.023 \times 10^{23}}{10^{10} \times 365 \times 24 \times 60 \times 60}=1,908,00$ years.
Q. A chamber of constant volume contains hydrogen gas. When the chamber is immersed in a bath of melting ice $\left(0^{\circ} \mathrm{C}\right),$ the pressure of the gas is $1.07 \times 10^{2} \mathrm{kPa} .$ What pressure will be indicated when the chamber is brought to $100^{\circ} \mathrm{C} ?$
[NCERT]
Ans.
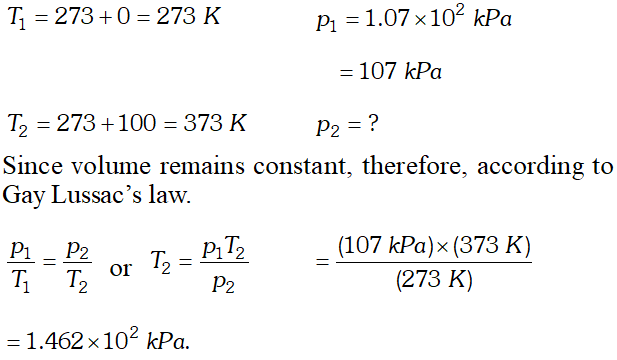
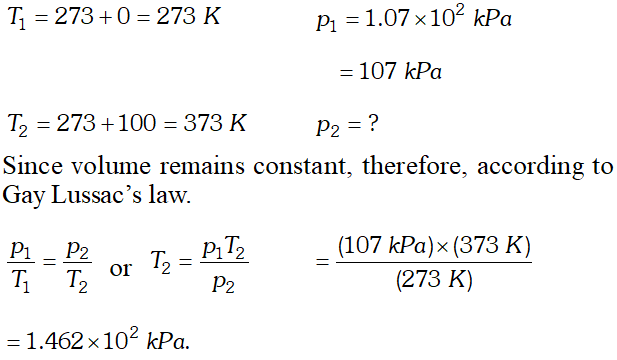
Q. What would be the S.I. unit for the quantity $p V^{2} T^{2} / n ?$
[NCERT]
Ans. $\frac{p V^{2} T^{2}}{n}=\frac{\left(N m^{-2}\right)\left(m^{3}\right)^{2}(K)^{2}}{m o l}$
$=N m^{4} K^{2} m o l^{-1}$
Q. What is the value of universal gas constant ? What is its value in SI units ?
Ans. $R=8.314 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$
Q. Explain the significance of the vander Waal’s parameters ?
Ans. $^{c} a^{\prime}$ is a measure of the magnitude of the intermolecular forces of attraction while $b$ is a measure of the effective size of the gas molecules.
Q. Give most common application of Dalton's law.
Ans. The air pressure decreases with increases in altitude. That is why jet aeroplane flying at high altitude need pressurization of the cabin so that partial pressure of oxygen is sufficient for breathing.
Q. $N_{2} O$ and $C O_{2}$ have the same rate of diffusion under same conditions of temperature and pressure. Why?
Ans. Both have same molar mass $\left(=44 g m o l^{-1}\right)$. According to Graham’s law of diffusion, rates of diffusion of different gases are inversely proportional to the square root of their molar masses under same conditions of temperature and pressure.
Q. At what temperature will oxygen molecules have the same K.E. as ozone molecules at $30^{\circ} \mathrm{C} ?$
Ans. At $30^{\circ} \mathrm{C},$ kinetic energy depends only on absolute temperature and not on the identity of a gas.
Q. Which two postulates of the kinetic molecular theory are only approximations when applied to real gases?
Ans. (i) Inter molecular forces between molecules are negligible.
(ii) Molecules of a gas have negligible volumes.
Q. Account for the following properties of gases on the basis of kinetic molecular theory,
(i) High compressibility
(ii) Gases occupy whole of the volume available to them.
Ans. (i) High compressibility is due to large empty spaces between the molecules.
(ii) Due to absence of attractive forces between molecules, the molecules of gases can easily separate from one another.
Q. Critical temperature of carbon dioxide and $C H_{4}$ are $31.1^{\circ} \mathrm{C}$ and $-81.9^{\circ} \mathrm{C}$ respectively. Which of these has stronger intermolecular forces and why? $\quad$
[NCERT]
Ans. Higher the critical temperature, more easily the gas can be liquefied i.e. greater are the intermolecular forces of attraction. Therefore, $\mathrm{CO}_{2}$ has stronger intermolecular forces than $\mathrm{CH}_{4}$
Q. (i) What will be the pressure exerted by a mixture of $3.2 \mathrm{g}$ of methane and $4.4 \mathrm{g}$ of carbon dioxide contained in a $9 d m^{3}$ flask at $27^{\circ} \mathrm{C} ?$
(ii) Give two example of Covalent solids.
OR
(i) Calculate the total number of electrons present in 1.4 $g$ of nitrogen gas.
(ii) Which of the two gases, ammonia and hydrogen chloride, will diffuse faster and by what factor?
(iii) Why urea has sharp melting point but glass does not?
Ans. $(\mathrm{i}) \mathrm{pCH}_{4}=\frac{n R T}{\mathrm{V}}=\frac{3.2}{16} \times \frac{0.0821 \mathrm{L} \operatorname{atm} \mathrm{K}^{-1} \mathrm{mol}^{-1} \times 300 \mathrm{K}}{9 \mathrm{L}}$$p C H_{4}=\frac{0.2 \times 24.63}{9}=\frac{4.926}{9}=0.547 \mathrm{atm}$
$p C H_{4}=\frac{0.2 \times 24.63}{9}=\frac{4.926}{9}=0.547 \mathrm{atm}$
(ii) Boron and silicon are example of Covalent solids.
Or
(i) $28 g$ of Nitrogen gas contains $2 \times 7 \times 6.023 \times 10^{23}$ electrons. $1+1$
$\begin{array}{llll}{1.4} & {g} & {\text { of }} & {\text { Nitrogen }} & {\text { gas }} & {\text { contains }}\end{array}$
$\frac{2 \times 7 \times 6.023 \times 10^{23}}{28} \times 1.4$
$=\frac{2 \times 7 \times 6.023 \times 10^{23}}{20}=\frac{84.32 \times 10^{23}}{20}$
$=4.2161 \times 10^{23}$ electrons
(ii) $N H_{3}$ will diffuse faster
$\frac{r_{N H_{3}}}{r_{H C l}}=\sqrt{\frac{36.5}{17}}=\sqrt{2.14}=1.46$ times faster.
(iii) Urea is a crystalline solid therefore it has sharp melting point whereas glass does not have sharp melting point because it is amorphous, i.e., does not have regular three dimensional structure.
Q. What will be the minimum pressure required to compress $500 d m^{3}$ of air at 1 bar to $200 d m^{3}$ at $30^{\circ} \mathrm{C} ? \quad
Ans.
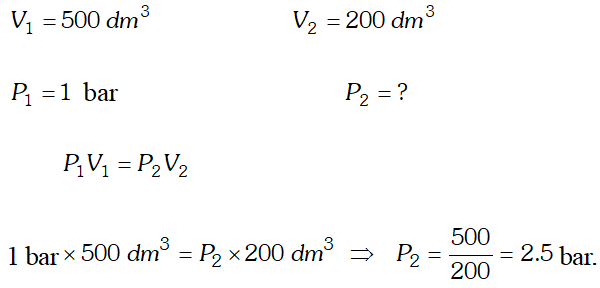
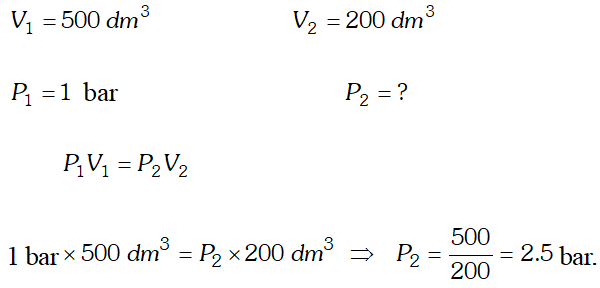
Q. A manometer is connected to a gas containing bulb. The open arm reads 43.7 cm whereas the arm connected to the bulb reads 15.6 cm. If the barometric pressure is 743 mm mercury, what is the pressure of the bulb reads 15.6 cm. If the barometric pressure is 743 mm mercury, what is the pressure of the gas in bar ?
[NCERT]
Ans. Pressure of gas $=$ Atmospheric pressure $+$ Difference between levels of $\mathrm{Hg}$
$=743 \mathrm{mm}+(43.7 \mathrm{cm}-15.6 \mathrm{cm})=74.3 \mathrm{cm}+28.1 \mathrm{cm}$
$P=102.4 \mathrm{cm} P$ in bar $=\frac{102.4}{76}=1.347 \mathrm{bar}$
Q. Calculate the number of moles of hydrogen $\left(H_{2}\right)$ present in a $500 \mathrm{cm}^{3}$ sample of hydrogen gas at a pressure of $760 \mathrm{mm}$ Hg and $27^{\circ} \mathrm{C}$.
[NCERT]
Ans. $P V=n R T, \quad P=1$ atm, $\quad V=500 \mathrm{cm}^{3}, \quad n=?$
$R=82.1 \mathrm{atm} \mathrm{cm}^{3} \mathrm{K}^{-1} \mathrm{mol}^{-1}, T=300 \mathrm{K}$
$n=\frac{1 a t m, \times 500 \mathrm{cm}^{3}}{\left(82.1 \mathrm{atm} \mathrm{cm}^{3} \mathrm{K}^{-1} \mathrm{mol}^{-1}\right) \times(300 \mathrm{K})}=0.02 \mathrm{mol}$
Q. $34.05 \mathrm{ml}$ of phosphorus weight $0.0625 \mathrm{g}$ at $546^{\circ} \mathrm{Cand} 1$
bar pressure. What is the molar mass of phosphorus?
Or
In terms of Charle's law explain why $-273^{\circ} \mathrm{C}$ is the lowest possible temperature.
[NCERT]
Ans.
$p V=n R T$
1 bar $\times \frac{34.05}{1000} L=\frac{0.0625}{M} \times 0.083 \times 819 K$
$M=\frac{0.0625 \times 0.083 \times 819 K \times 1000}{34.05}=\frac{4248.5625}{34.05}$
$M=124.77 \mathrm{g} \mathrm{mol}^{-1}$
Or
Charle's plotted the volume against temperature in $^{\circ} C$. These plots when extraplotted intersect the temperature axis at the same point $-273^{\circ} \mathrm{C} .$ He concluded that all gases at this temperature could have zero volume and below this temperature volume would be negative. It shows $-273^{\circ} \mathrm{C}$ is lowest temperature attainable.
Q. A vessel of $120 \mathrm{mL}$ capacity contains a certain amount of gas at $35^{\circ} \mathrm{C}$ and 1.2 bar pressure. The gas is transferred to another vessel of volume $180 \mathrm{mL}$ at $35^{\circ} \mathrm{C} .$ What would be its pressure?
[NCERT]
Ans. Since temperature and amount of gas remains constant, therefore, Boyle’s law is applicable.
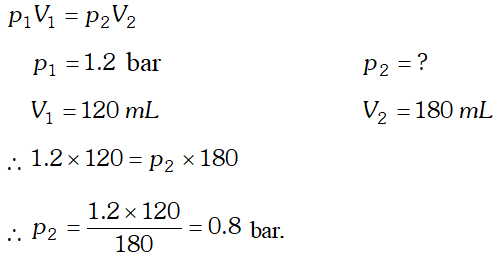
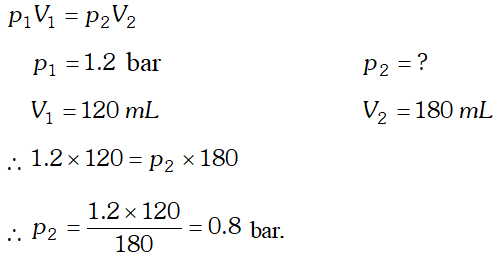
Q. A balloon is filled with hydrogen at room temperature. It will burst if pressure exceeds 0.2 bar. If at 1 bar pressure the gas occupies 2.27 L volume, upto what volume can the balloon be expanded ?
[NCERT]
Ans. According to Boyle’s law, at constant temperature,
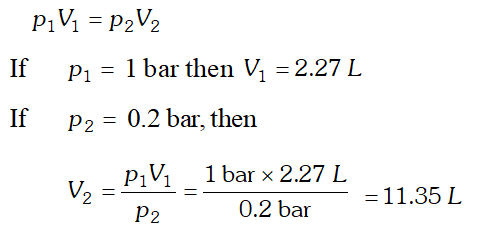Since balloon bursts at 0.2 bar pressure, the volume of the balloon should be less than 11.35 L.
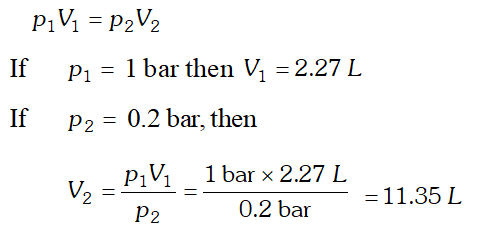Since balloon bursts at 0.2 bar pressure, the volume of the balloon should be less than 11.35 L.
Q. A student forgot to add the reaction mixture to the round bottomed flask at $27^{\circ} \mathrm{C}$ but instead, he/she placed the flask on the flame. After a lapse of time, he realized his mistake, and using a pyrometer, he found the temperature of the flask was $477^{\circ} \mathrm{C} .$ What fraction of air would have been expelled out?
[NCERT]
Ans. Suppose volume of vessel $=V c m^{3}$
i.e., volume of air in the flask at $27^{\circ} \mathrm{C}=\mathrm{Vcm}^{3}$
$\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}, \quad$ i.e., $\quad \frac{V}{300}=\frac{V_{2}}{750} \quad$ or $\quad V_{2}=2.5 \mathrm{V}$
$\therefore$ Volume expelled $=2.5 \mathrm{V}-\mathrm{V}=1.5 \mathrm{V}$
Fraction of air expelled $=\frac{1.5 \mathrm{V}}{2.5 \mathrm{V}}=\frac{3}{5}$
Q. What is the difference in pressure between the top and bottom of a vessel $76 \mathrm{cm}$ deep at $27^{\circ} \mathrm{C}$ when filled with (i) water (ii) mercury? Density of water at $27^{\circ} \mathrm{C}$ is $0.990 \mathrm{g} \mathrm{cm}^{-3}$ and that of mercury is $13.60 \mathrm{g} \mathrm{cm}^{-3}$
Ans. Pressure $=$ height $\times$ density $\times g$
Case (i). Pressure
$=76 \mathrm{cm} \times 0.99 \mathrm{g} / \mathrm{cm}^{3} \times 981 \mathrm{cm} / \mathrm{s}^{2}$
$=7.38 \times 10^{4}$ dynes $\mathrm{cm}^{-2}$
$=0.073$ atm $\left(1 \mathrm{atm}=1.013 \times 10^{6} \text { dynes } \mathrm{cm}^{-2}\right)$
Case (ii). Pressure
$=76 \mathrm{cm} \times 13.6 \mathrm{g} / \mathrm{cm}^{3} \times 981 \mathrm{cm} / \mathrm{s}^{2}$
$=1.013 \times 10^{6}$ dynes $\mathrm{cm}^{-2}=1 \mathrm{atm}$
Q. An iron cylinder contains helium at a pressure of $250 \mathrm{kPa}$ at $300 K .$ The cylinder can withstand a pressure of
$1 \times 10^{6}$ pa. Theroom in which cylinder is placed catches fire. Predict whether the cylinder will blow up before it melts or not. (M.P. of the cylinder $=1800 K$ )
Ans.
Q. On a ship sailing in a pacific ocean where temperature is $23.4^{\circ} \mathrm{C},$ a balloon is filled with $2 \mathrm{L}$ air. What will be the volume of the balloon when the ship reaches Indian ocean, where temperature is $26.1^{\circ} \mathrm{C} ? \quad$
[NCERT]
Ans. According to Charles’ law
$\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}$
$V_{1}=2 L$
$V_{2}=?$
$T_{1}=273+23.4=296.4 \mathrm{K} \quad T_{2}=273+26.1=299.1$
$\therefore V_{2}=\frac{V_{1} T_{2}}{T_{1}}=\frac{2 L \times 299.1 K}{296.4 K}=2.018 L$
Q. What is the increase in volume when the temperature of 800 $m L$ of air increases from $27^{\circ} \mathrm{C}$ to $47^{\circ} \mathrm{Cunder}$ constant pressure of $1 \mathrm{bar} ?$
[NCERT]
Ans. Since the amount of gas and the pressure remains constant, Charles’ law is applicable. i.e.
$\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}$
$V_{1}=800 \mathrm{mL}$
$V_{2}=?$
$T_{1}=273+27=300 K ; \quad T_{2}=273+47=320 K$
$\frac{800 m L}{300 K}=\frac{V_{2}}{320 K}$
or $\quad V_{2}=\frac{(800 \mathrm{mL})}{(300 \mathrm{K})} \times(320 \mathrm{K})=853.3 \mathrm{mL}$
Increase in volume of air $=853.3-800=53.3 \mathrm{mL}$
Q. A cylinder containing cooking gas can withstand a pressure of 14.9 atmospheres. The pressure gauge of the cylinder indicates 12 atmosphere at $27^{\circ} \mathrm{C} .$ Due to sudden fire in the building, temperature starts rising. At what temperature will the cylinder explode?
Ans. since gas is confined in a cylinder, its volume will remain constan
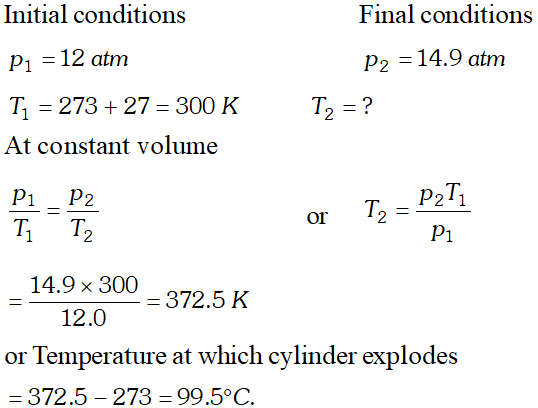
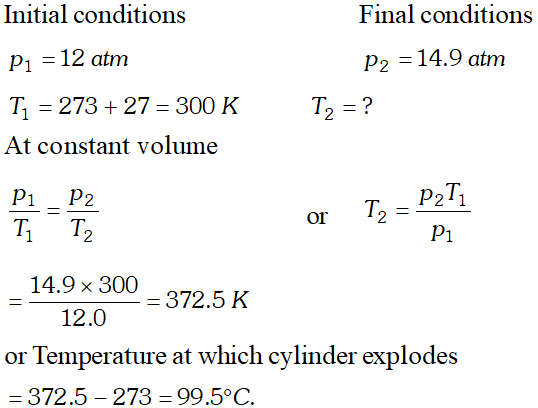
Q. What will be the pressure exerted by a mixture when $0.5 L$ of $H_{2}$ at 0.8 bar and $2.0 L$ of oxygen at 0.7 bar are introduced in 1 container at $27^{\circ} \mathrm{C}$.
[NCERT]
Ans.
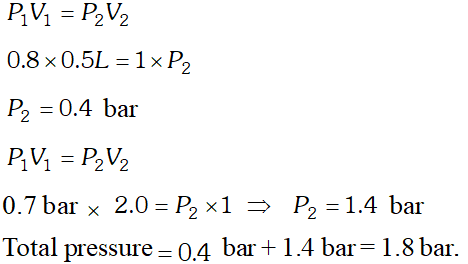
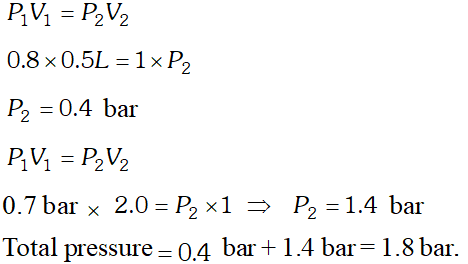
Q. Calculate the temperature of 4.0 moles of a gas occupying $6 d m^{3}$ at 3.32 bar $\left(R=0.083 \text { bar } d m^{3} K^{-1} \mathrm{mol}^{-1}\right)$
[NCERT]
Ans. According to ideal gas equation:
$p V=n R T$
$p=3.32$ bar, $V=5 d m^{3}, n=4.0 \mathrm{mol}$
$R=0.083$ bar $d m^{3} K^{-1} \mathrm{mol}^{-1}$
$T=\frac{p V}{n R}=\frac{3.32 \text { bar } \times 5 d m^{3}}{4.0 \mathrm{mol} \times 0.083 \text { bar } d m^{3} K^{-1} \mathrm{mol}^{-1}}=50 \mathrm{K}$
Q. When $2 g$ of gas $A$ is introduced into an evacuated flask kept at $25^{\circ} \mathrm{C},$ the pressure is found to be 1 atm. If $3 \mathrm{g}$ of another gas $B$ is then added to the same flask the total pressure becomes 1.5 atm at the same temperature. Assuming ideal behaviour of gases, calculate the ratio of molecular weights $M_{A}: M_{B}$
Ans. According to ideal gas equation,
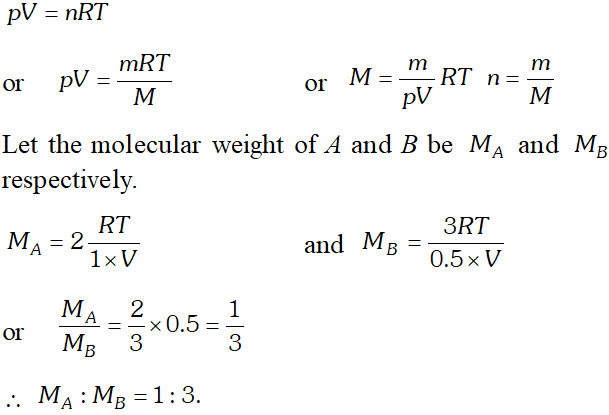
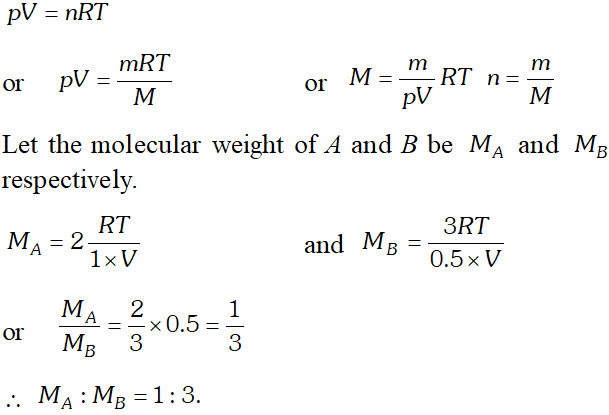
Q. An evacuated glass vessel weighs $50.0 \mathrm{g}$ when empty, $148.0 \mathrm{g}$ when filled with a liquid of density $0.98 \mathrm{g} \mathrm{m}^{-1}$ and $50.5 \mathrm{g}$ when filled with an ideal gas at $760 \mathrm{mm} \mathrm{Hg}$ at $300 \mathrm{K}$. Determine the molecular weight of the gas.b
Ans. Weight of liquid $=148-50=98 g$
Density of liquid $=0.98 g m l^{-1}$
$\therefore$ Volume of liquid $=\frac{98}{0.98}=100 \mathrm{ml}$
Weight of gas $=50.5-50.0=0.5 g$
Volume $=\frac{100}{1000} L, P=1$ atm, $T=300 K$
$p V=n R T$ or $p V=\frac{W}{M} R T$
$\frac{1 \times 100}{1000}=\frac{0.5}{M} \times 0.082 \times 300$
$\therefore M=123.15 g \mathrm{mol}^{-1}$
Q. At $0^{\circ} \mathrm{C},$ the density of a gaseous oxide at 2 bar pressure is same as that of nitrogen at 5 bar. What is the molecular mass of the gaseous oxide? $\quad$
[NCERT]
Ans. Calculation of density of $N_{2}$ at 5 bar and $0^{\circ} \mathrm{C}$
$d=\frac{P M}{R T}=\frac{5(\text { bar }) \times 28\left(g m o l^{-1}\right)}{0.0831\left(L \text { bar } K^{-1} \mathrm{mol}^{-1}\right) \times 273.15(K)}$
$=6.168 g L^{-1}$
Calculation of molar mass of gaseous oxide
$M=\frac{d R T}{P}$
$=\frac{6.168\left(g L^{-1}\right) \times 0.0831\left(L \text { bar } K^{-1} \mathrm{mol}^{-1}\right) \times 273.15(K)}{2}$
$=70.0 \mathrm{g} \mathrm{mol}^{-1}$
Q. Density of a gas is found to be $5.46 g / d m^{3}$ at $27^{\circ} \mathrm{C}$ and 2 bar pressure. What will be its density at S.T.P.?
[NCERT]
Ans.
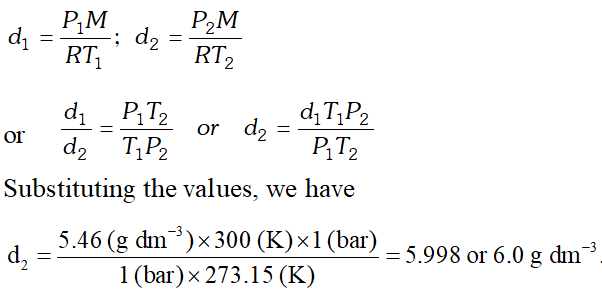
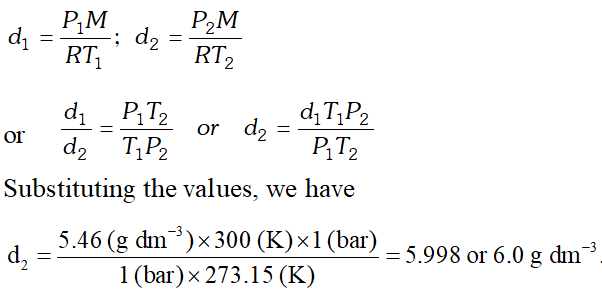
Q. What will be pressure exerted by a mixture of $3.2 \mathrm{g}$ of methane and $4.4 \mathrm{g}$ of carbon dioxide contained in a $9 \mathrm{dm}^{3}$ flask at $27^{\circ} \mathrm{C} ?$
Ans. $p=\frac{n}{V} R T=\frac{w}{M} \frac{R T}{V}$
$p_{C H_{4}}=\left(\frac{3.2}{16} m o l\right) \frac{0.0821 d m^{3} a t m K^{-1} m o l^{-1} \times 300 K}{9 d m^{3}}$
$=0.55 \mathrm{atm}$
$p_{\mathrm{CO}_{2}}=\left(\frac{4.4}{44} \mathrm{mol}\right) \frac{0.0821 \mathrm{dm}^{3} \mathrm{atm} \mathrm{K}^{-1} \mathrm{mol}^{-1} \times 300 \mathrm{K}}{9 \mathrm{dm}^{3}}$
$=0.27 \mathrm{atm}$
$p_{\text {Total }}=0.55+0.27=0.82 \mathrm{atm}$
Q. Calculate the total pressure in a mixture of $8 g$ of $O_{2}$ and $4 g$
of $H_{2}$ confined in a vessel of $d m^{3}$ at $27^{\circ} C, R=0.083$ bar $d m^{3} K^{-1} \mathrm{mol}^{-1} .$ Atomic mass of $O=16 u, H=1 u$
[NCERT]
Ans. $p V=n R T$
$p \times 1=\frac{8}{32} \times 0.083 \times 300=\frac{24.9}{4}=6.225$ bar
$p \times 1=\frac{4}{2} \times 0.083 \times 300=49.80 \mathrm{bar}$
Total Pressure $=6.225+49.80=56.025$ bar
Q. For 10 minutes each, at $27^{\circ} \mathrm{C}$, from two identical holes, nitrogen and an unknown gas are leaked into common vessel of 3 L capacity. The resulting pressure is 4.18 bar and the mixture contains 0.4 mole of nitrogen. What is the molar mass of the unknown gas ?
[NCERT]
Ans.
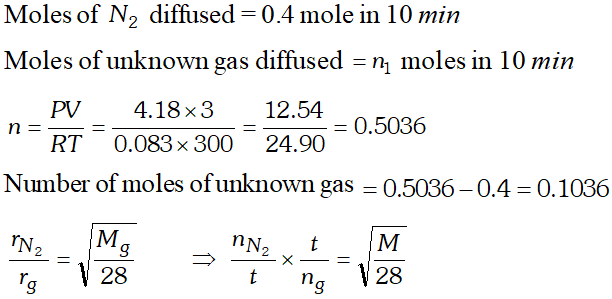
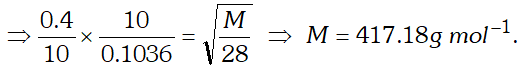
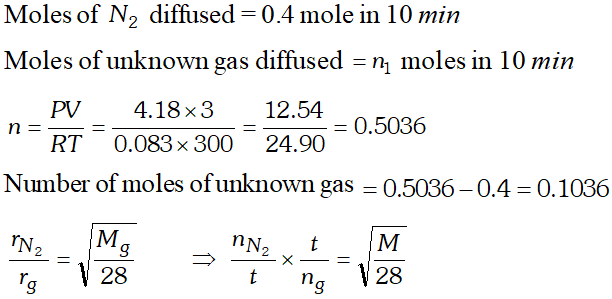
Q. Pay load is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the pay load when a balloon of radius $10 \mathrm{m},$ mass $100 \mathrm{kg}$ is filled with helium at 1.66 bar at $27^{\circ} \mathrm{C}$. (Density of air $=1.2$ $\left.k g m^{-3} \text { and } R=0.083 \text { bar } d m^{3} K^{-1} \mathrm{mol}^{-1}\right)$
[NCERT]
Ans. Pay load is the difference between the mass of displaced air and the mass of the balloon.
Volume of ballon $=\frac{4}{3} \pi r^{3}$
Radius of balloon, $r=10 \mathrm{m}$
$V=\frac{4}{3} \times 3.14 \times(10)^{3}=4186.7 \mathrm{m}^{3}$
Mass of displaced air $=4186.7 \mathrm{m}^{3} \times 1.2 \mathrm{kg} \mathrm{m}^{-3}$
$=5024.04 \mathrm{kg}$
Moles of gas present $=\frac{p V}{R T}$
$=\frac{1.66 \times 4186.7 \times 10^{3}}{0.083 \times 300}=279.11 \times 10^{3} \mathrm{mol}$
Mass of helium present $=279.11 \times 10^{3} \times 4$
$=1116.44 \times 10^{3} g=1116.4 \mathrm{kg}$
Mass of filled balloon $=100+1116.4=1216.4 \mathrm{kg}$ Pay load $=$ mass of displaced air - Mass of balloon
$=5024.4-1216.44=3807.6 \mathrm{kg}$
Q. A balloon of diameter $20 \mathrm{m}$ weights $100 \mathrm{kg} .$ Calculate the pay load if it is filled with $H e$ at 1.1 atm and $27^{\circ} \mathrm{C}$. Density of air is $1.2 \mathrm{kg} \mathrm{m}^{-3}\left(\mathrm{R}=0.082 \mathrm{dm}^{3} \mathrm{atm} \mathrm{K}^{-1} \mathrm{mol}^{-1}\right)$
Ans. Volume of balloon,
$V=\frac{4}{3} \pi r^{3} r=10 m$
$\therefore V=\frac{4}{3} \times 3.14 \times(10)^{3}=4187 \mathrm{m}^{3}$
Mass of displaced air $=4187 \mathrm{m}^{3} \times 1.2 \mathrm{kg} \mathrm{m}^{-3}$
$=5024.44 \mathrm{kg}$
Moles of gas present, $n=\frac{P V}{R T}=\frac{1 \times 4187 \times 10^{3}}{0,082 \times 298}$
$=171.3 \times 10^{3} \mathrm{mol}$
Mass of He present $=171.3 \times 10^{3} \times 4$
$=685.3 \times 10^{3} g$
$=685.3 \mathrm{kg}$
Mass of filled balloon $=100+685.3=785.3 \mathrm{kg}$
Pay load $=$ Mass of displaced air - Mass of balloon $=5024.4-785.3=4239.1 \mathrm{kg}$
Q. Using vander Waal's equation, calculate the constant " $a$ ' when two moles of a gas confined in a $4 L$ flask exerts a pressure of 11.0 atmospheres at a temperature of $300 K .$ The value of $b$ is $0.05 L \mathrm{mol}^{-1}$
Ans. $\left(p+\frac{a n^{2}}{V^{2}}\right)(V-n b)=n R T$
$n=2 \mathrm{mol}, V=4 L, p=11 \mathrm{atm}$
$T=300 K, b=0.05 L m o l^{-1}$
Substituting the values
$\left(11+\frac{a \times 4}{16}\right)(4-2 \times 0.05)=2 \times 0.082 \times 300$
$\frac{176+4 a}{16} \times 3.9=49.2$
$(176+4 a) 3.9=49.2 \times 16$
$15.6 a=787.2-686.4$
$a=6.4616 \mathrm{atm} \mathrm{L}^{2} \mathrm{mol}^{-2}$
Q. $34.05 \mathrm{mL}$ of phosphorus vapour weigh $0.0625 \mathrm{g}$ at $546^{\circ} \mathrm{C}$ and 1 bar pressure. What is the molar mass of phosphorus?
[NCERT]
Ans. Mole of phosphorus vapour $(n)=\frac{P V}{R T}$
$=\frac{1(\text {bar}) \times 34.05 \times 10^{-3}(L)}{0.0831\left(\text {bar } L K^{-1} \mathrm{mol}^{-1}\right) \times 819.15(K)}=5.0 \times 10^{-4}$
Let molar mass of phosphorus be $M g m o l^{-1}$
$\therefore$ Mole of phosphorus vapour $=\frac{0.0625}{M}$
Now, $\frac{0.0625}{M}=5.0 \times 10^{-4}$ or $M=\frac{0.0625}{5.0 \times 10^{-4}}$
$=125 g \mathrm{mol}^{-1}$
Q. The drain cleaner, Drainex contain small bits of aluminium which react with caustic soda to produce hydrogen. What volume of hydrogen at $20^{\circ} \mathrm{C}$ and 1 bar will be released when $0.15 g$ of aluminium reacts?
[NCERT]
Ans. The chemical reaction taking place is
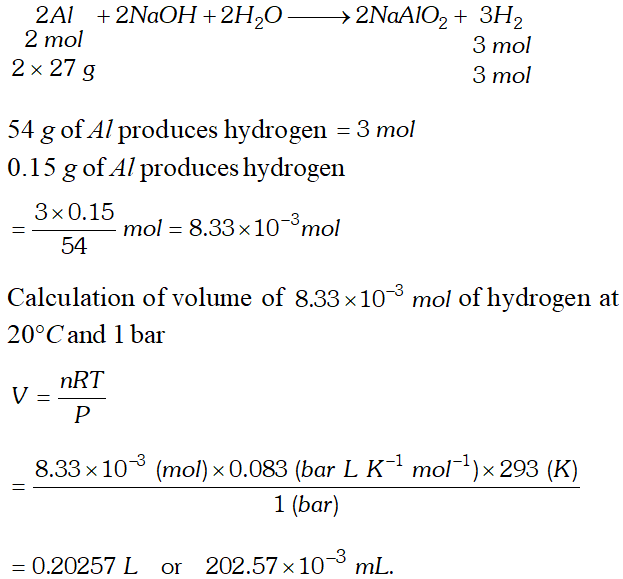
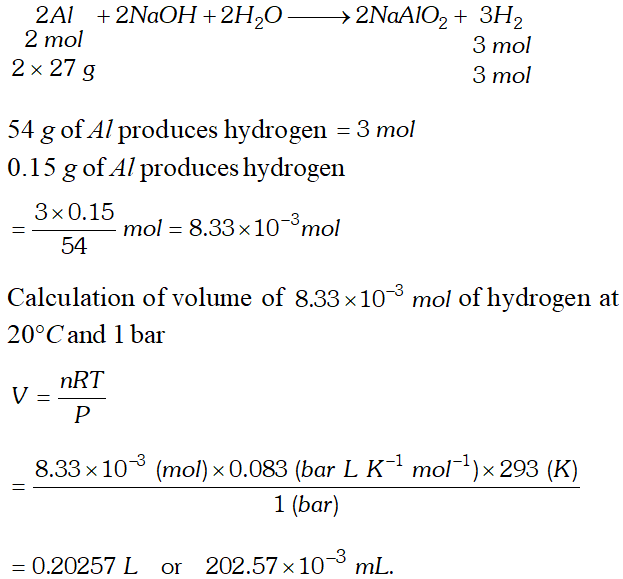
Q. For a real gas obeying vander Waal's equation, a graph is plotted between $P V_{m}(y \text { -axis })$ and $P(x \text { -axis })$ where $V_{m}$ is the molar volume. Find $y$ -intercept of the graph.
Ans. For a real gas, the plot of $P V_{m}$ vs $P$ can be of the type $A$ or $B$ but at the point of intercept, $P=0$ and at any low pressure, vander Waal's equation reduce to ideal gas equation.
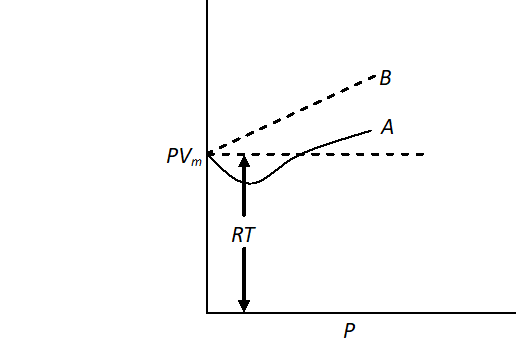$\mathrm{PV}=\mathrm{nRT}$ or $\mathrm{PV}_{\mathrm{m}}=\mathrm{RT}$
Hence, $y$ -intercept of graph will be $=R T$
$\mathrm{PV}=\mathrm{nRT}$ or $\mathrm{PV}_{\mathrm{m}}=\mathrm{RT}$
Hence, $y$ -intercept of graph will be $=R T$
Q. (i) State Graham's law of diffusion. Arrange the gases $\mathrm{CO}_{2}, \mathrm{SO}_{2}, \mathrm{NO}_{2}$ in order of increasing rates of diffusion.
(ii) What is the volume of $0.300 \mathrm{mol}$ of ideal gas at $60^{\circ} \mathrm{C}$ and 0.821 atm pressure?
Ans. (i) For statement of the Graham's law. Molar mass of:
$\mathrm{CO}_{2}=44 \mathrm{u} ; \mathrm{SO}_{2}=64 \mathrm{u}$ and $\mathrm{NO}_{2}=46 \mathrm{u}$
As $r_{d i f f} \propto \frac{1}{\sqrt{M}},$ therefore, larger the molar mass lesser
will be the rate of diffusion under similar condition. Thus, increasing order of rates of diffusion is
$r_{S O_{2}}
Q. Through two ends of a glass tube of length $200 \mathrm{cm} \mathrm{HCl}$ and $N H_{3}$ gases are allowed to enter. At what distance ammonium chloride will first appear?
[NCERT]
Ans. $\frac{r_{N H_{3}}}{r_{H C l}}=\frac{l_{1}}{200-l_{1}}=\sqrt{\frac{M_{H C l}}{M_{N H_{3}}}}=\sqrt{\frac{36.5}{17}}$
$\frac{l_{1}}{200-l_{1}}=\sqrt{2.147}=1.465$
$l_{1}=293-1.465 l_{1} ; 2.465 l_{1}=293$
$l_{1}=\frac{293}{2.465}=118.88 \mathrm{cm}$
$200-l_{1}=200-118.88=81.12 \mathrm{cm}$ from $\mathrm{HCl}$ end.
Q. Equal volumes of two gases A and B diffuse through a porous pot in 20 and 10 seconds respectively. If the molar mass of A be 80, find the molar mass of B.
[NCERT]
Ans. $\frac{r_{A}}{r_{B}}=\sqrt{\frac{M_{B}}{M_{A}}}$ or $\frac{t_{B}}{t_{A}}=\sqrt{\frac{M_{B}}{M_{A}}}$
$t_{A}=20$ sec, $t_{B}=10$ sec, $M_{A}=80, M_{B}=?$
$\frac{10}{20}=\sqrt{\frac{M_{B}}{80}}$
$M_{B}=\frac{80}{4}=20 g \mathrm{mol}^{-1}$
Q. A mixture of hydrogen and oxygen at one bar pressure contains 20% by weight of hydrogen. Calculate the partial pressure of hydrogen.
[NCERT]
Ans. As the mixture $H_{2}$ and $O_{2}$ contains $20 \%$ by weight of
hydrogen, therefore, if $H_{2}=20 g,$ then $O_{2}=80 g$
$n_{H_{2}}=\frac{20}{2}=10$ moles, $n_{O_{2}}=\frac{80}{32}=2.5$ moles
$p_{H_{2}}=\frac{n_{H_{2}}}{n_{H_{2}}+n_{O_{2}}} \times P_{\text {total }}=\frac{10}{10+2.5} \times 1$ bar $=0.8$ bar.
Q. Calculate the total pressure in a mixture of $8 g$ of oxygen and $4 g$ of hydrogen confined in a vessel of $1 d m^{3}$ at $27^{\circ} \mathrm{C}$ $\left(R=0.083 \text { bar } d m^{3} K^{-1} \mathrm{mol}^{-1}\right)$
[NCERT]
Ans. Partial pressure of oxygen gas,
$p=\frac{n R T}{V}$
$n=\frac{8}{32}$ mol, $\quad \mathrm{V}=1 \mathrm{dm}^{3}, T=300 \mathrm{K}$
$p_{\left(O_{2}\right)}=\frac{8 \times 0.083 \times 300}{32 \times 1}=6.225$ bar
Partial pressure of hydrogen gas
$p=\frac{n R T}{V}$
$n=\frac{4}{2}=2 m o l$
$p\left(H_{2}\right)=\frac{2 \times 0.083 \times 300}{1}=49.8 \mathrm{bar}$
Total pressure $=p_{\left(O_{2}\right)}+p_{\left(H_{2}\right)}$
$=6.225+49.8=56.025$ bar
Q. A vessel of $1.00 \mathrm{dm}^{3}$ capacity contains $8.00 \mathrm{g}$ of oxygen and $4.00 \mathrm{g}$ of hydrogen at $27^{\circ} \mathrm{C} .$ Calculate the partial pressure of each gas and also the total pressure in the container $\left(R=0.083 \text { bar } d m^{3} K^{-1} \mathrm{mol}^{-1}\right)$
[NCERT]
Ans. Let the partial pressure of hydrogen be $P_{H_{2}}$ and the partial
pressure of oxygen be $P_{O_{2}}$
The number of mole of hydrogen $\left(n_{1}\right)=\frac{4}{2}=2$ mole
The number of mole of oxygen $\left(n_{2}\right)=\frac{8}{32}=0.25$ mole
Now, applying ideal gas equation for each gas $p_{H_{2}} \times V=n_{1} R T$
$p_{H_{2}}=\frac{n_{1} R T}{V}=\frac{2 \times 0.083 \times 300}{1}=49.8$ bar
Similarly, $p_{O_{2}} V=n_{2} R T$
$p_{O_{2}}=\frac{n_{2} R T}{V}=\frac{0.25 \times 0.083 \times 300}{1}=6.225 \mathrm{bar}$
Total pressure of gaseous mixture
$=p_{H_{2}}+p_{O_{2}}=49.8+6.225=56.025$ bar.
Q. Calculate (i) Average kinetic energy of $32 g$ of methane molecules at $27^{\circ} \mathrm{C} R=8.314 \mathrm{JK}^{-1} \mathrm{mol}^{-1}$
(ii) Root mean square speed and (ii) Most probable speed of methane molecule at $27^{\circ} \mathrm{C}$
Ans. (i) Average kinetic energy is given as $E_{k}=\frac{3 n R T}{2}$
Here, $n=\frac{32}{16}=2 ; R=8.314 \mathrm{JK}^{-1} \mathrm{mol}^{-1} ; T=300 \mathrm{K}$
$\therefore E_{k}=\frac{3 \times 2 \times 8.314 \times 300}{2}=7482.6 \mathrm{J}$
(ii) Root mean square speed is given as
$u_{r m s}=\sqrt{\frac{3 R T}{M}}$
Here use $R=8.314 \times 10^{7}$ ergs $K^{-1} \mathrm{mol}^{-1}$ to get speed in
$\mathrm{cm} \mathrm{s}^{-1}$
$u_{m s}=\sqrt{\frac{3 \times 8.314 \times 10^{7} \times 300}{16}}=68385.85 \mathrm{cm} s^{-1}=68.38 \mathrm{ms}^{-1}$
(iii) Most probable speed
$(\alpha)=\frac{u_{r m s}}{1.224}=\frac{683.8}{1.224}=558.7 \mathrm{ms}^{-1}$
Q. Calculate root mean square speed $(r m s)$ of ozone which is kept in a closed vessel at $20^{\circ} \mathrm{C}$ and a pressure of $82 \mathrm{mm}$ of $H g$
Ans. Volume occupied by $1 \mathrm{mol}$ of $\mathrm{O}_{3}$ at $20^{\circ} \mathrm{C}$ and $82 \mathrm{mm}$ pressure is calculated by applying general gas equation,
$\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}$
$\therefore \quad V_{2}=\frac{P_{1} V_{1} T_{2}}{T_{1} P_{2}}=\frac{76 \times 22400 \times 293}{273 \times 82}=22281.92 \mathrm{cm}^{3}$
Now, $u=\sqrt{\frac{3 P V}{M}}$
Here, we use $P$ in dyne/cm$^{2}, P=82 \times 13.6 \times 981$ dyne/cm$^{2}$
$\therefore u=\sqrt{\frac{3 \times 82 \times 13.6 \times 981 \times 22281.92}{48}}=3.90 \times 10^{4} \mathrm{cm} \mathrm{s}^{-1}$
Q. (i) Explain Boyle’s law with the help of Kinetic theory of gases.
(ii) An open beaker at $27^{\circ} \mathrm{C}$ is heated to $477^{\circ} \mathrm{C} .$ What fraction of air would have been expelled out?
[NCERT]
Ans. (i) The kinetic theory of gases assumes that pressure of gas is due to collision of gas molecules with the walls of the container. The more will be frequency of collision, more will be pressure. The reduction in volume of gas increases no. of molecules per unit volume to which pressure is directly proportional. Therefore, the volume of the gas is reduced if pressure is increased or pressure is inversely proportional to volume.
$\frac{1}{2} m u^{2}=\frac{3}{2} k T$
$p=\frac{1}{3} \frac{N}{V} m u^{2}$ or $p=\frac{2}{3} \frac{N}{V} \times \frac{1}{2} m u^{2}=\frac{2}{3} \frac{N}{V} \times \frac{3}{2} k T$
$\Rightarrow p V=N k T \Rightarrow P \alpha \frac{1}{V}$
It can be seen that at a constant temperature for a fixed number of gas molecules, the pressure is inversely proportional to volume.
(ii) $\frac{T_{1}}{T_{2}}=\frac{n_{1}}{n_{2}} \quad \begin{array}{cc}{T_{1}=27^{\circ} C+273} & {=300 K} \\ {T_{2}=477+273=} & {750 K}\end{array}$
$\frac{300 K}{750 K}=\frac{n_{1}}{n_{2}}, \quad \frac{n_{1}}{n_{2}}=\frac{2}{5} b v$
fraction of air escaped $=1-\frac{2}{5}=\frac{3}{5}$
Q. At which temperature average velocity of oxygen molecules is equal to the rms velocity at $27^{\circ} \mathrm{C} ?$
Ans. Average velocity $=\sqrt{\frac{8 R T}{\pi M}}$
Root mean square velocity
$=\sqrt{\frac{3 R T}{M}}=\sqrt{\frac{3 R \times 300 K}{M}}$
For equal values, $\sqrt{\frac{8 R T}{\pi M}}=\sqrt{\frac{3 R \times 300}{M}}$
or $\quad \frac{8 R T}{\pi M}=\frac{3 R \times 300}{M}$ or $\frac{8 T}{\pi}=900$
or $\quad T=353.57 K=80.57^{\circ} \mathrm{C}$
Q. At a constant temperature, a gas occupies a volume of 200 mL at a pressure of 0.720 bar. It is subjected to an external pressure of 0.900 bar. What is the resulting volume of the gas ?
[NCERT]
Ans. Boyle’s law is applicable as the amount and temperature are unaltered
$p_{1} V_{1}=p_{2} V_{2}$
or $p_{1} / p_{2}=V_{2} / V_{1}$ 'Substituting the values
0.720 bar/ 0.900 bar $=V_{2} / 200 \mathrm{mL}$
$V_{2}=\frac{720}{900} \times 200 m L=160 m L$
Boyle’s law is manifested in the working of many devices used in daily life such as cycle pump, aneroid barometer and tyre pressure gauge etc.
Q. Calculate the number of nitrogen molecules present in 2.8 g of nitrogen gas.
[NCERT]
Ans. Number of moles of nitrogen
$=2.8 g / 28 g \mathrm{mol}^{-1}=0.1 \mathrm{mol}$
Number of nitrogen molecules $=0.1 \mathrm{mol} \times 6.022 \times 10^{23}$
$m o l^{-1}=6.022 \times 10^{22}$
Q. If the density of a gas at the sea level at $0^{\circ} \mathrm{C}$ is $1.29 \mathrm{kg} \mathrm{m}^{-3}$, what is its molar mass? (Assume that pressure is equal to 1 bar)
[NCERT]
Ans. $p V_{m}=R T$ or $p M / d=R T$ or $M=d R T / p$
$=\frac{1.29 \mathrm{kg} m^{-3} \times 8.314 \mathrm{NmK}^{-1} \mathrm{mol}^{-1} \times 273.15 \mathrm{K}}{1.0 \times 10^{5} \mathrm{Nm}^{-2}(\mathrm{or} P a)}$
$=\frac{1.29 \times 8.314 \times 273.15 k g m o l^{-1}}{1 \times 10^{5}}$
$=0.0293 \mathrm{kg} \mathrm{mol}^{-1}$ or molar mass is $29.3 \mathrm{g} \mathrm{mol}^{-1}$
Q. Which of the two gases, ammonia and hydrogen chloride, will diffuse faster and by what factor ?
[NCERT]
Ans. $r_{N H_{3}} / r_{H C 1}=\left(M_{H C 1} / M_{N H_{3}}\right)^{1 / 2}$
$=(36.5 / 17)^{1 / 2}=1.46$ or $r_{N H_{3}}=1.46 r_{H C 1}$
Thus ammonia will diffuse 1.46 times faster than hydrogen chloride gas.
Q. A 2.5 flask contains 0.25 mol each of sulphur dioxide, and nitrogen gas at $27^{\circ} \mathrm{C}$. Calculate the partial pressure exerted by each gas and also the total pressure.
[NCERT]
Ans. Partial pressure of sulphur dioxide,
$p_{S O_{2}}=n R T / V$
$=\frac{0.25 \mathrm{mol} \times 8.314 \mathrm{JK}^{-1} \mathrm{mol}^{-1} \times 300 \mathrm{K}}{2.5 \times 10^{-3} \mathrm{m}^{3}}$
$=2.49 \times 10^{5} \mathrm{Nm}^{-2}=2.49 \times 10^{5} \mathrm{Pa}$
Similarly $p_{N_{2}}=2.49 \times 10^{5} \mathrm{Pa}$
Following Dalton's law $p_{\text {Total }}=p_{N_{2}}+p_{S O_{2}}$
$=2.49 \times 10^{5} P a+2.49 \times 10^{5} P a=4.98 \times 10^{5} P a$
Q. An open vessel at $27^{\circ} \mathrm{C}$ is heated until $\frac{3}{5}$ parts of the air in it has been expelled. Assuming that the volume of the vessel remains constant, find the temperature to which the vessel has been heated.
Ans. As the vessel is open, pressure and volume remain constant. Thus, if $n_{1}$ moles are present at $T_{1}$ and $n_{2}$ moles are present at $T_{2},$ we can write
$P V=n_{1} R T_{1} ; P V=n_{2} R T_{2}$
Hence, $n_{1} R T_{1}=n_{2} R T_{2}$ or $n_{1} T_{1}=n_{2} T_{2}$
or, $\quad \frac{n_{1}}{n_{2}}=\frac{T_{2}}{T_{1}}$
Suppose the no. of moles of air originally present $=n$
After heating, no. of moles of air expelled $=\frac{3}{5} n$
$\therefore$ No. of moles left after heating $=n-\frac{3}{5} n=\frac{2}{5} n$
Thus, $n_{1}=n, T_{1}=300 K ; n_{2}=\frac{2}{5} n, T_{2}=?$
$\frac{n}{\frac{2}{5} n}=\frac{T_{2}}{300}$ or $\frac{5}{2}=\frac{T_{2}}{300}$ or $, T_{2}=750 \mathrm{K}$
Alternatively, suppose the volume of the vessel $=V$
i.e. Volume of air initially at $27^{\circ} C=V$
Volume of air expelled $=\frac{3}{5} V$
$\therefore$ Volume of air left at $27^{\circ} \mathrm{C}=\frac{2}{5} \mathrm{V}$
However, on heating to $T^{\circ} K,$ it would become $=V$ As pressure remains constant, (vessel being open),
$\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}$ i.e. $\frac{2 / 5 \mathrm{V}}{300 \mathrm{K}}=\frac{\mathrm{V}}{T_{2}}$ or $T_{2}=750 \mathrm{K}$
Q. A glass bulb contains $2.24 L$ of $H_{2}$ and $1.12 L$ of $D_{2}$ at
S.T.P. It is connected to fully evacuated bulb by a stopcock with a small opening. The stopcock is opened for sometime and then closed. The first bulb now contains $0.10 \mathrm{g}$ of $D_{2} .$ Calculate the percentage composition by weight of the gases in the second bulb.
Ans. Weight of $2.24 \mathrm{L}$ of $\mathrm{H}_{2}$ at $\mathrm{S} . T . P .=0.2 \mathrm{g}$
(Mol. mass of $\left.H_{2}=2\right)=0.1 \mathrm{mol}$
Weight of $1.12 \mathrm{L}$ of $D_{2}$ at $S . T . P .=0.2 \mathrm{g}$
(Mol. mass of $\left.D_{2}=4\right)=0.05 \mathrm{mol}$
As number of moles of two gases are different but V and T are same, therefore, their partial pressures will be different, i.e., in the ratio of their number of moles. Thus,
$\frac{P_{H_{2}}}{P_{D_{2}}}=\frac{n_{H_{2}}}{n_{D_{2}}}=\frac{0.1}{0.5}=2$
Now, $D_{2}$ present in the first bulb $=0.1 g$ (Given)
$D_{2}$ diffused into the second bulb
$=0.2-0.1=0.1 g=0.56 L$ at $S . T . P .$
Now, $\frac{r_{H_{2}}}{r_{D_{2}}}=\frac{P_{H_{2}}}{P_{D_{2}}} \times \sqrt{\frac{M_{D_{2}}}{M_{H_{2}}}}$
Or, $\frac{v_{H_{2}}}{t} \times \frac{t}{v_{D_{2}}}=\frac{P_{H_{2}}}{P_{D_{2}}} \times \sqrt{\frac{M_{D_{2}}}{M_{H_{2}}}}$
$\frac{v_{H_{2}}}{t} \times \frac{t}{0.56 L}=2 \times \sqrt{\frac{4}{2}}$
or $\quad v_{H_{2}}=1.584 L=0.14 g$ of $H_{2}$
$\therefore$ Weight of the gases in 2 nd bulb
$=0.10 g\left(D_{2}\right)+0.14 g\left(H_{2}\right)=0.24 g$
Hence, in the 2 nd bulb,
$\%$ of $D_{2}$ by weight $=\frac{0.10}{0.24} \times 100=41.67 \%$
$\%$ of $H_{2}$ by weight $=100-41.67=58.33 \%$
Q. An $L P G$ (Liquefied Petroleum Gas) cylinder weights 14.8 kg when empty. When full, it weighs 29.0 kg and shows a pressure of 2.5 atm. In the course of use at $27^{\circ} \mathrm{C},$ the mass of the full cylinder is reduced to 23.2 kg. Find out the volume of the conditions, and the final pressure inside the cylinder. Assume $L P G$ to be $n$ -butane with normal boiling point of $0^{\circ} \mathrm{C}$
Ans. Weight of $L P G$ originally present $=29.0-14.8$ $=14.2 \mathrm{kg}$
Pressure $=2.5$ atm Weight of LPG present after use $=23.2-14.8$ $=8.4 \mathrm{kg}$
since volume of the cylinder is constant, applying
since volume of the cylinder is constant, applying
$p V=n R T$
$\frac{p_{1}}{p_{2}}=\frac{n_{1}}{n_{2}}=\frac{W_{1} / M}{W_{2} / M}=\frac{W_{1}}{W_{2}}$
$\frac{2.5}{p_{2}}=\frac{14.2}{8.4}$
$p_{2}=\frac{2.5 \times 8.4}{14.2}=1.48 \mathrm{atm}$
or Weight of used gas $=14.2-8.4=5.8 \mathrm{kg}$
Moles of gas $=\frac{5.8 \times 10^{3}}{58}=100$ moles
Normal conditions
$p=1$ atm;
$T=273+27=300 K$
Volume of 100 moles of $L P G$ at 1 atm and $300 \mathrm{K}$
$V=\frac{n R T}{p}=\frac{100 \times 0.082 \times 300}{1}=2460$ litre
$V=2.460 \mathrm{m}^{3}$
Q. The compressibility factor for one mole of a vander Waals gas at $0^{\circ} \mathrm{C}$ and 100 atm pressure is found to be $0.5 .$ Assume that the volume of gas molecule is negligible, calculate yander
Ans. Compressibility factor
$Z=\frac{p V}{R T} ; \quad 0.5=\frac{100 \times V}{0.082 \times 273}$
$\therefore V=\frac{0.5 \times 0.082 \times 273}{100}=0.1119 L$
If volume of molecules is negligible i.e. $b$ is negligible vander Waals' equation:
$\left(p+\frac{a}{V^{2}}\right)(\mathrm{V})=R T$
or $p V=R T-a / V$ or $a=R T V-P V^{2}$
$=(0.082 \times 273 \times 0.1119)-(100 \times 0.1119 \times 0.1119)$
$=1.253 \mathrm{atm} L^{2} \mathrm{mol}^{-2}$