Get important questions from Thermodynamics and Heat for Class 11 exams. View all Physics important questions for all the chapters. These important questions from thermodynamics class 11 physics will play significant role in clearing concepts of Physics. This question bank is designed by expert faculties keeping NCERT in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions from heat and thermodynamics chapter. Learn all the concepts of thermodynamics from these important questions of class 11 Physics. Click Here for Detailed Notes of Heat and Thermodynamics along with other chapters and subjects.
Q. How is the mean kinetic energy of a gas related to its temperature?
Ans. Mean kinetic energy is proportional to its absolute temperature.
Q. Although the root mean square speed of gas molecules is of the order of the speed of sound in that gas, yet on opening a bottle of ammonia in one corner of a room its smell takes time in reaching the other corner. Explain why?
Ans. The molecules of ammonia continuously collide with one another. Hence they are not able to advance in one particular direction speedly.
Q. There are n molecules of gas in a box. If the number of molecules is increased to 2n. What will be the effect on the pressure of the gas? On the kinetic energy of the gas? On the root mean square speed of the molecules?
Ans. 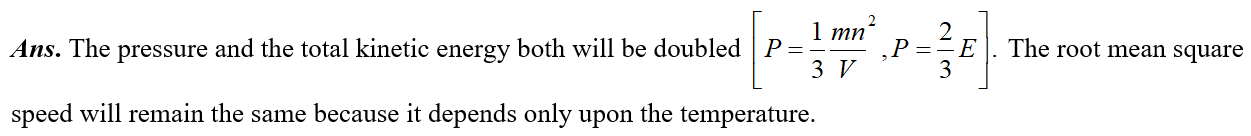
Q. On which factor does the average kinetic energy of gas molecules depend : nature of the gas, absolute temperature, volume.
Ans. It depends only upon the absolute temperature and is directly proportional to it $\left(=\frac{3}{2} K T\right)$
Q. Equal masses of monoatomic gas and diatomic gas at the same temperature are given equal quantities of heat. Which gas will have greater temperature rise?
Ans. Monoatomic gas will have greater temperature rise because a monoatomic gas has only translational energy but diatomic gas has both translational as well as rotational energy.
Q. The graph shows the variation of the product PV with respect to the pressure (P) of given masses of three gases A, B and C. The temperature is kept constant, state with proper arguments which of these gases is ideal.
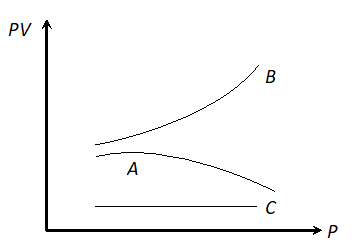
Ans. Gas C is ideal, because PV is constant for this gas. It means the gas C obeys Boyle’s law at all pressures.
Q. There is a temperature known as Boyle's temperature ( $\left.T_{\mathrm{B}}\right)$ for each real gas at which it behaves like an ideal gas. But if gas temperature T is less than $\mathrm{T}_{\mathrm{B}}$ then does it behaves like ideal gas.
Ans. No, because gas does not behave like an ideal gas if $T>T_{B}$ and $T
Q. What does universal gas constant signifies.
Ans. Universal gas constant signifies the work done by (or on) a gas per mole per kelvin.
Q. The molecules of a gas are 2n a state of continuous, rapid and random motion. They move in all directions with different speeds. What is the range of their speeds?
Ans. Zero to infinite.
Q. Two different gases have exactly the same temperature. Does this mean that their molecules have same r.m.s. speed?
Ans. When the two gases have exactly the same temperature, the average kinetic energy per molecule $\left(=\frac{1}{2} m c^{2}=\frac{3}{2} k T\right)$ for each gas is the same. But as the different gases may have molecules of different masses, the r.m.s. speed (c) of molecules of different gases shall be different.
Q. Distinguish between average speed and r.m.s. speed. If three molecules have speed u1, u2, u3 what will be their average speed and r.m.s. speed.
Ans. Average speed is the arithmetic mean of the speeds of the molecules.
$\therefore$ Average speed $=\frac{u_{1}+u_{2}+u_{3}}{3}$ But r.m.s. speed is the root mean square speed and is defined as the square root of the mean of the squares of different speeds of the individual molecules. 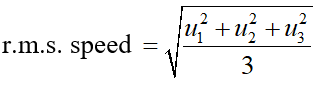
Q. A gas is filled in a cylinder fitted with a piston at a definite temperature and pressure. Explain on the basis of kinetic theory : on pulling the piston out, the pressure of gas decreases.
Ans. On pulling the piston out, the volume of the cylinder for the given gas increases. Due to which the molecules of gas get more space to move about. As a result of which less molecules will collide with the wall of cylinder per second and hence less momentum is transferred to the wall per second. In addition to it, now these collisions take place on the larger area of the walls. Due to both these reasons, the pressure decreases.
Q. State law of equipartition of energy.
Ans. According to this law, for any dynamical system in thermal equilibrium, the total energy is distributed equally amongst all the degrees of freedom and the energy associated with each molecule per degree of freedom is $\frac{1}{2} k T$, and hence a constant. (Here k is Boltzmann constant and T is temperature of the system).
Q. Obtain the relation between degree of freedom of a gas and ratio of two principal specific heats of the gas.
Ans. Suppose a polyatomic gas molecule has
n degrees of freedom.
Total energy associated with a gram molecule of the gas 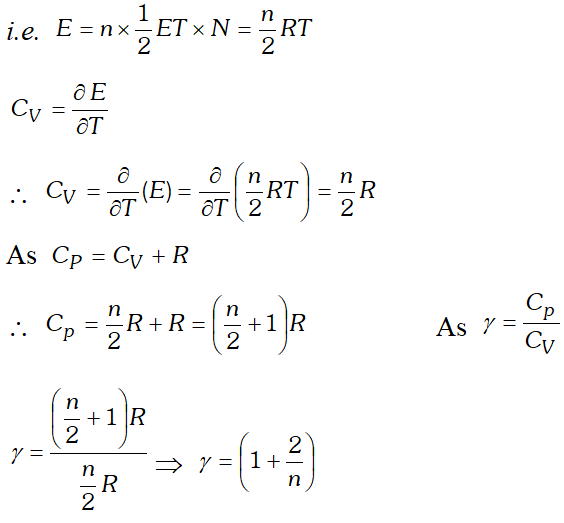 This is the relation between $\gamma$ and n. Hence the value of for a polyatomic gas can be determined from degree of freedom n.
This is the relation between $\gamma$ and n. Hence the value of for a polyatomic gas can be determined from degree of freedom n. Q. Why the molecular motion of the molecules ceases at zero kelvin?
Ans. We know kinetic energy of a molecule is proportional to the absolute temperature i.e. $\frac{1}{2} m c^{2} \propto T$ At $T=0$ $\frac{1}{2} m c^{2}=0$ since $\frac{1}{2} m \neq 0 \quad \therefore c=0$ Thus molecular motion ceases at zero kelvin.
Q. Explain the concept of temperature on the basis of kinetic theory?
Ans. According to kinetic theory of gases, the pressure exerted by the gas is given by $P=\frac{1}{3} \frac{m N}{V} c^{2} \ldots \ldots$ (i) Where $m=$ Mass of one molecule, $N=$ Number of molecules present in volume $V$ and $\frac{1}{c^{2}}=$ Mean square velocity exerted by the gas is given by $P=\frac{1}{3} \frac{m N}{V} c^{2} \ldots \ldots$ (i) Where $m=$ Mass of one molecule, $N=$ Number of molecules present in volume $V$ and$\bar{c}^{2}=$ Meansquare velocity If $V$ is the volume of $1 g m$ molecule $(1$ mole) of a gas. Then $N$ will be number of molecules present in volume $V$ i.e., $N$ will be Avogadro's number. Therefore, $m N$will be gram molecular mass. From eq. (i)$P V=\frac{1}{3} m N c^{2}$ But $m N=M=$ Gram molecular mass $P V=\frac{1}{3} M c^{2}$ ........(ii) But from ideal gas equation, $P V=R T$ .....(iii) From eq. (ii) and (iii) $\frac{1}{3} M c^{2}=R T$ .......(iv) $\overline{c^{2}}=\frac{3 R T}{M}$ $\overline{c^{2}} \propto T$ .........(v) Thus, the absolute temperature of a gas is directly proportional to the mean square velocity of the molecules of a gas. From eq. (iv) $\frac{2}{3} \times \frac{1}{2} M c^{2}=R T$ $\Rightarrow \frac{1}{2} M c^{2}=\frac{3}{2} R T$ $\frac{1}{2} m N c^{2}=\frac{3}{2} R T$ or $\frac{1}{2} m \bar{c}^{2}=\frac{3}{2} \frac{R}{N} T$ or $\frac{1}{2} m c^{2}=\frac{3}{2} K T$ or $E=\frac{3}{2} K T$ .........(vi) where $E=\frac{1}{2} m c^{2}=$ Mean kinetic energy of the molecule and $=\frac{R}{N}=$ constant $k$ is called Boltzmann's constant. From eq. (vi) $E \propto T$ Thus, the mean kinetic energy of a molecule is directly proportional to the absolute temperature of the gas. If $T=0$ then from eq. (v), $\bar{c}^{2}=0$ and from eq. (vi) $E=0$ Thus, the absolute zero is that temperature at which the r.m.s. velocity of the gas becomes zero. Since, can never be negative, therefore the value of absolute temperature T can never be negative. This is the reason due to which the lowest temperature on kelvin’s scale is assumed to be 0K.
Q. At what temperature does all molecular motions cease?
Ans. Zero kelvin (or Absolute zero $\left.=-273.13^{\circ} \mathrm{C}\right)$
Q. What is the nature of graph, taking $0^{\circ} \mathrm{C}$ along the $\mathrm{y}$ -axis and 'F along the x-axis. What is the slope of this graph?
Ans. Straight line of the form : $y=m x-c,\left[c=\frac{5}{9}(F-32)\right]$, having slope $=5 / 9$.
Q. How is the molar gas constant related to the principal gas constant?
Ans. R = Mr.
Q. Why temperature beyond $1200^{\circ} \mathrm{C}$ cannot be measured accurately by a platinum resistance thermometer?
Ans. Beyond $1200^{\circ} \mathrm{C},$ platinum begins to evaporate.
Q. Two bodies at different temperatures $\mathrm{T}_{1}$ and $\mathrm{T}_{2}$if brought in thermal contact do not necessarily settle to the mean temperature $\left(\frac{T_{1}+T_{2}}{2}\right)$
Ans. In thermal contact, heat flows from a body at higher temperature to the body at lower temperature till temperatures become equal. The final temperature can be the mean temperature of $\left(\frac{T_{1}+T_{2}}{2}\right)$ only
Q. Why platinum wire can be sealed into glass but not the copper wire?
Ans. Platinum has coefficient of expansion slightly less than that of crown glass but copper has greater thermal expansion coefficient. So, if a platinum wire is put into molten glass thus the platinum-wire fits into a hole in molten glass. Since glass contracts more than platinum, glass fixes on to the wire. But, since copper is more expansible than glass, the copper wire contracts more than the hole in the glass, hence the copper wire losens out.
Q. What is the ice-point on kelvin scale? If the temperature of body increases by $1^{\circ} \mathrm{C},$ what will be change in temperature on kelvin scale?
Ans. $273.15 K$ is the ice point on kelvin scale. The relation between kelvin scale and centigrade scale is given by $\left.T(K)=\theta^{(0} C\right)+273.15$. The increaments in the temperature on kelvin scale are the same as the those of the celsius scale. i.e. $1^{\circ} C=1 K$.
Q. Which single point is used as reference point in thermometer ?
Ans. This single reference point is triple point of the substance.
Q. An electric refrigerator transfers heat from the cold cooling coils to the warm surroundings. Is it against the second law thermodynamics ? Justify your answer ?
Ans. No, it is not against the second law. This is because external work is done by the compressor of this transfer of heat.
Q. Can the carnot engine be realised in practice ?
Ans. No, because carnot engine is an ideal heat engine, whose conditions are not realised in practice.
Q. Does the mass of body change when it is heated or cooled ?
Ans. Yes in heating or cooling, a body absorbs or loses energy. The mass will, therefore increase or decrease accordingly as per the relation $E=m c^{2}$
Q. It is possible to convert internal energy into work ?
Ans. Yes, for example, in explosion of a bomb, chemical energy (which is a form of internal energy) is converted into kinetic energy.
Q. An ideal gas is compressed at constant temperature, will its internal energy increase or decrease ?
Ans. No, because internal energy of an ideal gas depends only on temperature of the gas.
Q. In summer, when the valve of a bicycle tube is opened, the escaping air becomes cold. Why?
Ans. This happens due to adiabatic expansion of air of the tube of the bicycle.
Q. Why does a gas get heated on compression ?
Ans. Because work done in compressing the gas increases the internal energy of gas.
Q. Why are the brake-drums of a car heated when the car moves down a hill at constant speed ?
Ans. Since the speed of car is not increasing, the gravitational potential energy is converted into internal energy of the break drums which are heated.
Q. If an electric fan be switched in a closed room, will the air of the room be cooled ? If not, why have feel cold ?
Ans. The air will not be cooled, but will be heated because due to motion of the fan, the speed of air molecules will increase. In fact, we feel cold due to evaporation of sweat.
Q. Is superheating of steam an isobaric process or isothermal process, and why ?
Ans. Isobaric, because during heating the temperature of steam does not remain constant.
Q. What are the limitations of first law of thermodynamics ?
Ans. The limitations are : (i)There is no information about the direction in which change takes place. (ii) It does not give any idea about the extent to which the change takes place.
Q. A gas does work during isothermal expansion ? What is the source of mechanical energy so produced ?
Ans. The energy required for doing work during isothermal expansion is acquired as heat by the gas from surroundings. Here $\quad \Delta Q=\Delta W i . e$. $\Delta U=0$
Q. What is the valve of work-done in a cyclic process ?
Ans. The work-done in a cyclic process is equal to the area of the closed curve on a P-V-diagram.
Q. Name the sink in case of steam engine ?
Ans. Atmosphere is the sink in most of the cases.
Q. Why can a ship not use the internal energy of sea water to operate its engine ?
Ans. For operation of a heat engine we require a sink at temperature lower than the source and of sufficiently high thermal capacity, which is not possible in sea.
Q. What do you understand by triple point of water ? Why it is unique ?
Ans. It is the temperature at which three phases of water namely ice, water and water vapour are equally stable and exist simultaneously. It is unique because it occurs at one single temperature $(273.16 K)$ at one single pressure of about $0.46 \mathrm{cm}$ of $\mathrm{Hg}$. column.
Q. Two cylinders A and B of equal capacity are connected to each other via a stop-cock. A contains a gas at standard temperature and pressure, B is completely evacuated. The entire system is thermally insulated. The stop-cock is suddenly opened. Answer the following (i) What is the final pressure of the gas in A and B? (ii) What is the change in internal energy of the gas ? (iii) What is the change in temperature of the gas? (iv) Do the intermediate state the system (before setting to final equilibrium state) be on its P-V-T surface ?
Ans. (i) Because an opening the stop-cock, the volume of gas is doubled at constant temperature as the system is thermally insulated, as the gas expands against zero pressure, so, in accordance to first law of thermodynamics, $\Delta U=0$. Further internal energy of an ideal gas depends on temperature only. Hence, temperature of gas will remain constant. Therefore pressure is halved i.e. pressure will reduce to 0.5 atm. (ii) An explained above, there is no change in internal energy. (iii)As explained above, there is also no change in temperature. (iv)No, since the process (called free expansion) is rapid and cannot be controlled. The intermediate states are non-equilibrium states and do not satisfy the gas equation. After a short time interval, the gas returns to equilibrium states which lies on its P-V-T surface.
Q. A Thermos bottle containing coffee is vigorously shaken. Considering coffee as a system (a) has heat been added to it? (b) has work been done on it? (c) has its internal energy changed? (d) does its temperature rise ?
Ans. (a) No, heat has not been transferred to the coffee as the coffee is in thermos flask which is insulated from the surroundings i.e. $\Delta Q=0$ (b) Yes, in shaking work is done on the coffee against viscous force $i . e . \Delta W$ is negative. (c) According to first law, $\Delta Q=\Delta U+\Delta W,$ however as here and negative, so be positive i.e. internal energy of coffee will increase. (d) Now, as internal energy of system depends upon its temperature i.e. , so temperature of the system (coffee) will also increase.
Q. Why is the conversion of heat into work not possible without a sink at lower temperature ?
Ans. If we want to convert heat energy continuously into work, a part of heat energy absorbed from the source has to be rejected. The rejection of heat energy is possible only if there is a body having temperature less than that of source. This body at lower temperature is called sink.
Q. What is meant by reversible engine ? Explain why the efficiency of reversible engine is maximum ?
Ans. The engine in which the process can be retraced at any stage of its operation by reversing the boundary conditions is called reversible. Its efficiency is maximum because in such a device dissipation of energy takes place against friction etc. only.
Q. Show that an adiabatic curve is always steeper than an isothermal curve.
Ans. Isothermal process : That thermal process in which the pressure and volume of the system (gas) change but temperature remains constant is called isothermal process. This process is achieved (a) if the gas is enclosed in a vessel whose walls are made of a highly conducting material and (b) the gas is compressed or allowed to expand very slowly.As temperature remains constant in an isothermal process, the gas equation is, PV = constant (K) Adiabatic process That thermal process in which pressure, volume and temperature of the system change but there is no exchange of heat between the system and the surroundings, is called an adiabatic process. This process is achieved (a) if the gas in enclosed in a vessel whose walls are made of a highly insulating material and (b) the gas is compressed or allowed to expand very quickly. The gas equation is, $P V^{\gamma}=$ constant, Slopes of isothermal and adiabatic curves The slope of an isothermal or adiabatic curve is given by $\frac{d P}{d V}$. (a) For an isothermal process, $P V=k$ Differentiating on both sides, we get, $P d V+V d P=0$ $\Rightarrow \frac{d P}{d V}=-\frac{P}{V}$ is slope of isothermal curve, $\left(\frac{d P}{d V}\right)=-\frac{P}{V}$ .............. (1) (b) For an adiabatic process, $P V^{\gamma}=K$ (constant) Differentiating on both sides, we get, $P_{\gamma} v^{\gamma-1} . d V+V^{\gamma} . d P=0$ $\Rightarrow V^{\gamma} d P=-\gamma P V^{\gamma-1} d V |$ $\therefore \frac{d P}{d V}=-\frac{\gamma P V^{\gamma-1}}{V^{\gamma}}=-\frac{\gamma P}{V}$ i.e. slope of adiabatic curve, $\left(\frac{d P}{d V}\right)_{A}=-\frac{\gamma P}{V}$ From equation ( 1) and $(2),$ we have, $\left(\frac{d P}{d V}\right)_{A}=\gamma\left(-\frac{P}{V}\right)=\gamma\left(\frac{d P}{d V}\right)_{I}$ As $\gamma$ is always greater than one, hence slope of adiabatic curve is greater than the slope of isothermal curve. In other words, an adiabatic curve is sleeper than an isothermal curve.
Q. State and explain first law of thermodynamics. Establish the relation between two principal specific heats of a gas on the basis of this law.
Ans. First law of thermodynamics : It is a statement of conservation of energy in thermodynamical process. According to it “when some quantity of heat (dQ) is supplied to system capable of doing external work, then the quantity of heat absorbed by the system (dQ) is equal to the sum of the increase in internal energy of the system (dU) and external work-done by the system (dW) ie. $d Q=d U+d W$ Relation between two principal specific heat of a gas : A gas has two specific heats Relation between two principal specific heat of a gas: A gas has two specific heats (i) Specific heat at constant volume $\left(C_{V}\right):$ It is the amount of heat required to raise the temperature of unit mass of a gas by $1^{\circ} C$ at constant volume. It is denoted by $C_{V}$ (ii) Specific heat at constant pressure $\left(\mathrm{C}_{P}\right):$ It is the amount of heat required to raise the temperature of unit mass of gas by $1^{\circ} \mathrm{C}$ at constant pressure. It is denoted by $C_{P}$. Let 1 mole of a gas is supplied $\Delta Q$ amount of heat at constant volume so that the temperature of the gas rises by $\Delta T$. $\therefore \Delta Q=1 \times C_{V} \times \Delta T=C_{V} \Delta T$ ...............(1) $\begin{array}{ll}{\text { As volume remains constant, }} \\ {d V=0} & {\therefore \Delta W=P \Delta V=0} \\ {\text { According to first law of thermodynamics, }} \\ {\Delta Q=\Delta U+\Delta W} \\ {\Rightarrow \Delta U=C_{V} \Delta T}\end{array}$ Now, let 1 mole of same gas is given an amount of heat $\Delta Q$ at constant pressure so as to increase the temperature by $\Delta T,$ then, $\Delta Q=1 \times C_{P} \times \Delta T \Rightarrow \Delta Q=C_{P} \Delta T$ .............(3) If $\Delta V$ is the change in volume at constant pressure, hen, $\Delta W=P \Delta V$ From first law, $\Delta Q=\Delta W+\Delta U$ $\Rightarrow \Delta Q=P \Delta V+\Delta U \quad \Rightarrow C_{P} \Delta T=P \Delta V+\Delta U$ $\Rightarrow P \Delta V+C_{V} \Delta T=C_{P} \Delta T[\text { From equation }(2)]$ $\Rightarrow\left(C_{P}-C_{V}\right) \Delta T=P \Delta V$ ...........(4) $\begin{array}{l}{\text { But from ideal gas equation, }} \\ {P V=R T \quad \text { ideal }} \\ {\text { From equation }(4), \text { we have, }}\end{array} \Rightarrow P \Delta V=R \Delta T$ $\left(C_{P}-C_{V}\right) \Delta T=R \Delta T$ This is known as Mayor's equation. Note (1) In above equation units of all quantities $\left(C_{P}, C_{V} \text { and } R\right)$ are Joule $m o l^{-1} K^{-1} .$ If $C_{P}$ and $d$ $C_{V}$ are expressed in units calorie $m o l^{-1} K^{-1},$ then $C_{P}-C_{V}=\frac{R}{J}$ (2) In above relation is expressed for one gram of gas, then, $C_{P}-C_{V}=\frac{r}{J}$ (3) As value of molar gas constant $R$ is $(+v e) 8.31$ Jmol $^{-1} K^{-1}$, it implies that $C_{P}>C_{V}$ and their difference in equal to $8.31 J \mathrm{mol}^{-1} K^{-1}$.
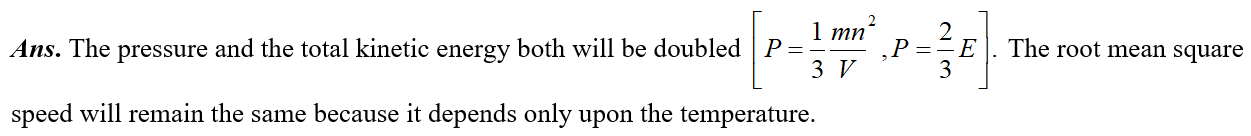

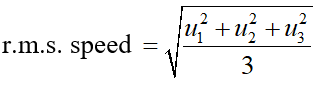
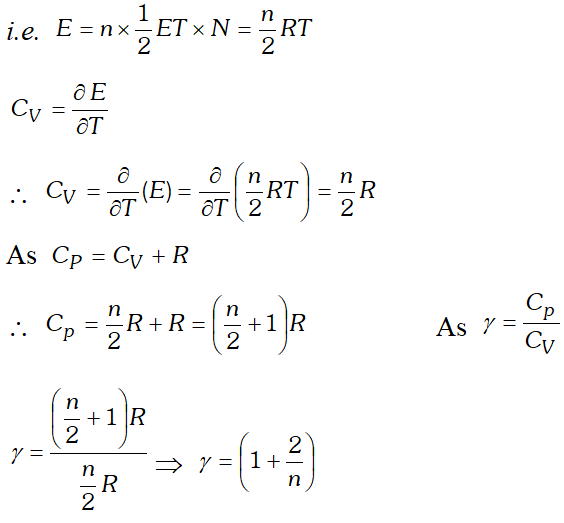 This is the relation between $\gamma$ and n. Hence the value of for a polyatomic gas can be determined from degree of freedom n.
This is the relation between $\gamma$ and n. Hence the value of for a polyatomic gas can be determined from degree of freedom n. 