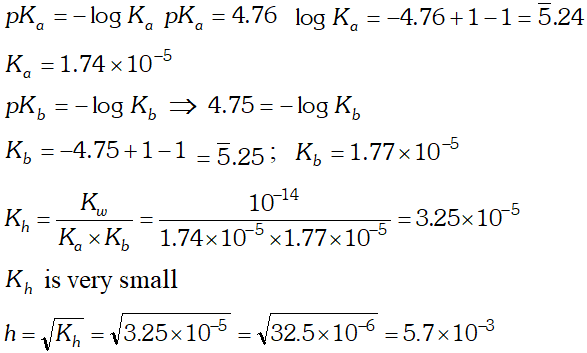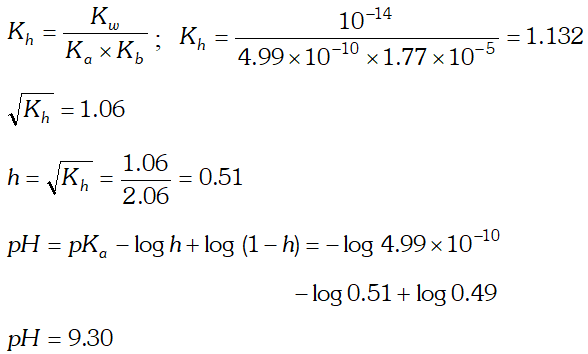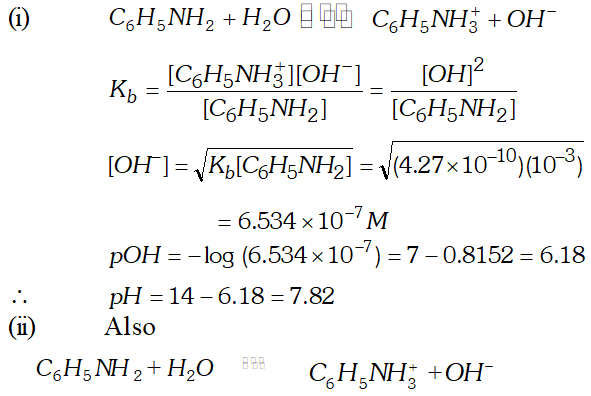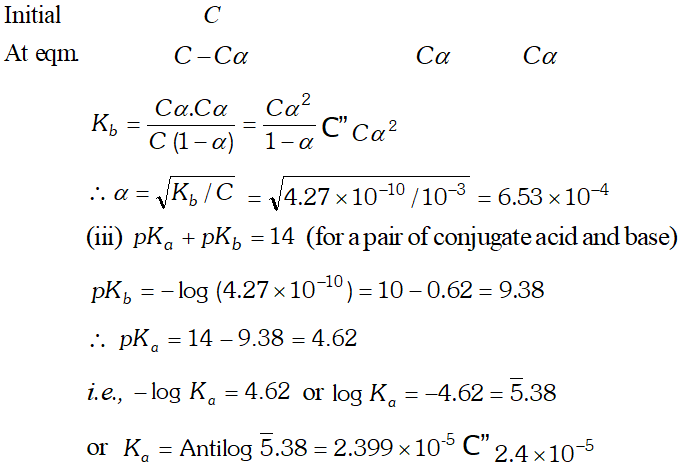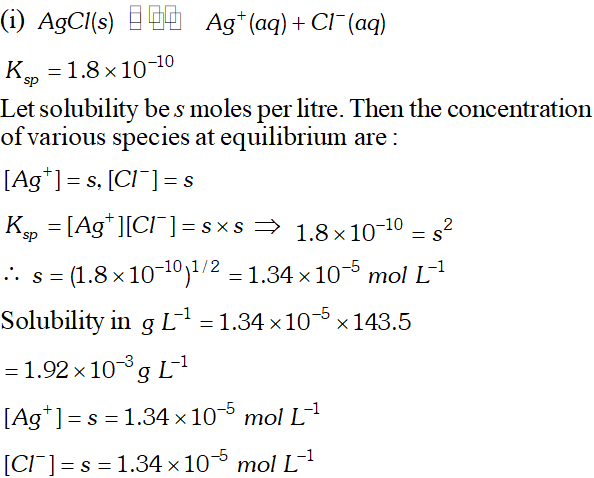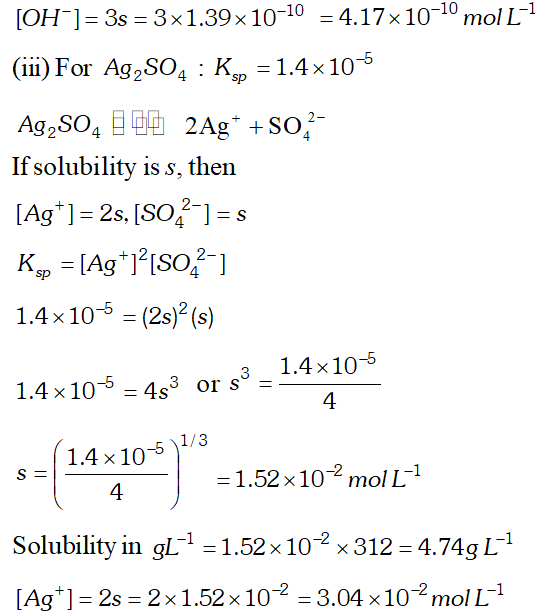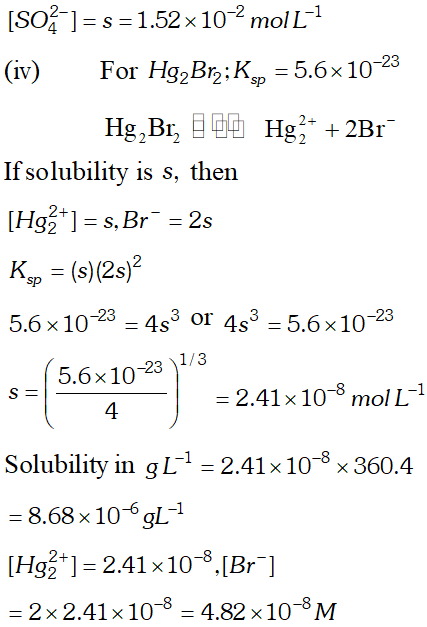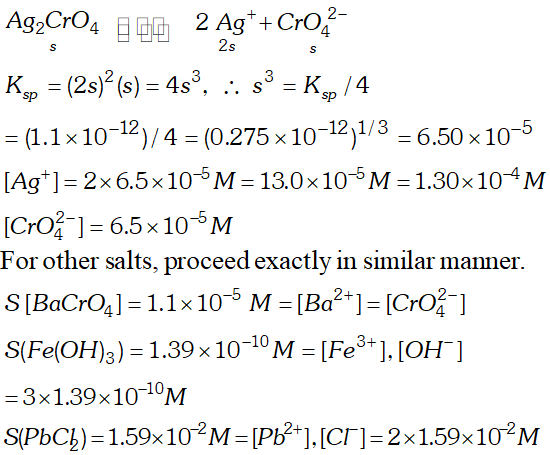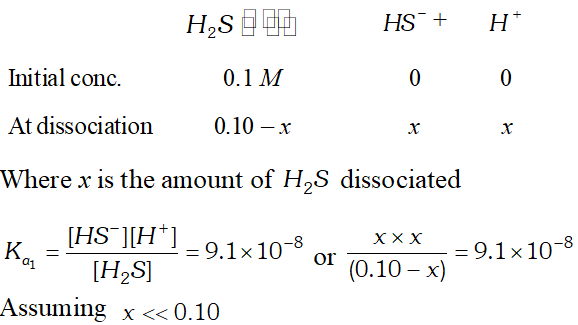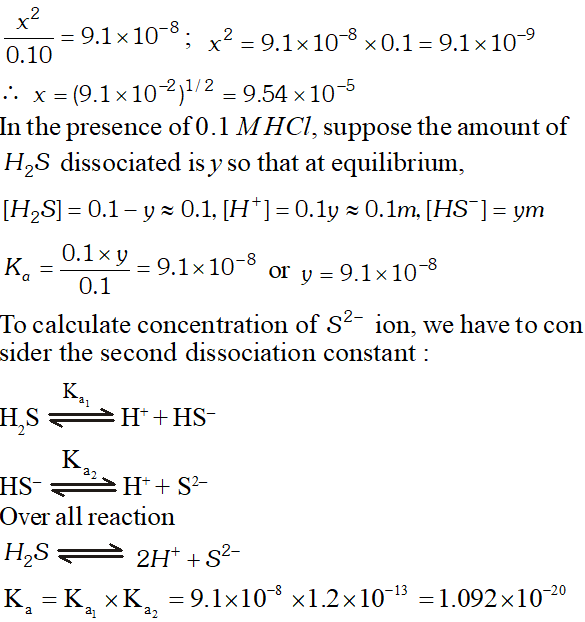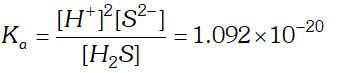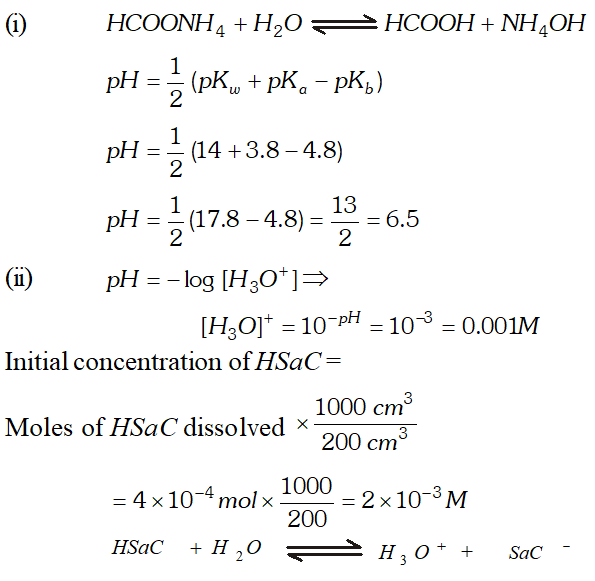Get Ionic Equilibrium important questions for Boards exams. Download or View the Important Question bank for Class 11 Chemistry. These important questions will play significant role in clearing concepts of Chemistry. This question bank is designed by NCERT keeping in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions for class 11 chemistry chapter wise CBSE. Click Here for Detailed Chapter-wise Notes of Chemistry for Class 11th, JEE & NEET. You can access free study material for all three subject’s Physics, Chemistry and Mathematics. Click Here for Detailed Notes of any chapter.
eSaral provides you complete edge to prepare for Board and Competitive Exams like JEE, NEET, BITSAT, etc. We have transformed classroom in such a way that a student can study anytime anywhere. With the help of AI we have made the learning Personalized, adaptive and accessible for each and every one. Visit eSaral Website to download or view free study material for JEE & NEET. Also get to know about the strategies to Crack Exam in limited time period. Q. How can we predict whether a precipitate will be formed or not on mixing two solutions ?
Ans. A precipitate will be formed if ionic product > solubility product.
Q. Define Lewis acid and Lewis base.
Ans. Lewis acid is a species which is electron deficient or positively charged Lewis base is a species which is electron rich, i.e., has lone pair of electron or is negatively charged.
Q. Define Bronsted acid and Bronsted base.
Ans. Bronsted acid can donate $H^{+}$ where as bronsted base can accept.
Q. ‘All Lewis bases are also Brosted base’. Is it true ? If yes, why ?
Ans. Yes, it is true, It is because Lewis bases are - velycharged or electron rich. They are bronsted bases also because they can accept $H^{+}$ easily.
Q. $p K_{a}$ values of acids $A, B, C, D$ are $1.5,3.5,2.0$ and $5.0 .$ Which of them is strongest acid?
Ans. Acid $^{\prime} A^{\prime}$ with $\mathrm{pKa}=1.5$ is strongest acid, lower the value of $P K_{a}$ stronger will be the acid.
Q. Predict if the solution of the following salts are neutral, acidic or basic: $N a C l, K B r, N a C N, N H_{4} N O_{3}, N a N O_{2}$ and $K F$
Ans. Neutral: $\mathrm{NaCl}, \mathrm{KBr} \quad$ Acidic : $\mathrm{NH}_{4} \mathrm{NO}_{3}$ Basic : $\mathrm{NaCN}, \mathrm{NaNO}_{2}$ and $\mathrm{KF}$
Q. What is the meant by conjugate acid-base pair ? Find the conjugate acid/base for the following species :
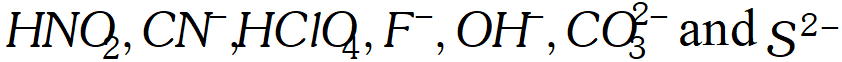
Ans. An acid-base which differ by a proton is called conjugate acid base pair. $\mathrm{NO}_{2}^{-}, \mathrm{HCN}, \mathrm{ClO}_{4}^{-}, \mathrm{HF}, \mathrm{H}_{2} \mathrm{O}(\mathrm{acid})$ or $\mathrm{O}^{2-}$ (base) $\mathrm{HCO}_{3}^{-}$ and $\mathrm{HS}^{-}$
Q. Which of the following are Lewis acids? $H_{2} O, B F_{3}, H^{+}, N H_{4}^{+}$
Ans. $p H=-\log \left[H^{+}\right]=-\log \left(3.8 \times 10^{-3}\right)$ $=-\log 3.8+3=3-0.5798=2.4202=2.42$
Q. The $p H$ of a sample of vinegar is $3.76 .$ Calculate the concentration of hydrogen ion in it.
Ans. $p H=-\log \left[H^{+}\right]$ or $\log \left[H^{+}\right]=-p H=-3.76=\overline{4} .24$ $\therefore\left[H^{+}\right]=$ Antilog $\overline{4} 24=1.738 \times 10^{-4} M=1.74 \times 10^{4} M$
Q. Which of the following combination would result in the formation of a buffer solution? (i) $\mathrm{NH}_{4} \mathrm{Cl}+\mathrm{NH}_{3}$ (ii) $\mathrm{CH}_{3} \mathrm{COOH}+\mathrm{HCl}$ (iii) $\mathrm{CH}_{3} \mathrm{COONa}+\mathrm{CH}_{3} \mathrm{COOH}$ (iv) $\mathrm{NH}_{3}+\mathrm{HCl}$ in the molar ratio of 2: 1 (v) $H C l+N a O H$
Ans. (i), ( iii), (iv)
Q. A $0.02 \mathrm{M}$ solution of pyridinium hydrochloride has $p H=3.44 .$ Calculate the ionization constant of pyridine.
Ans. 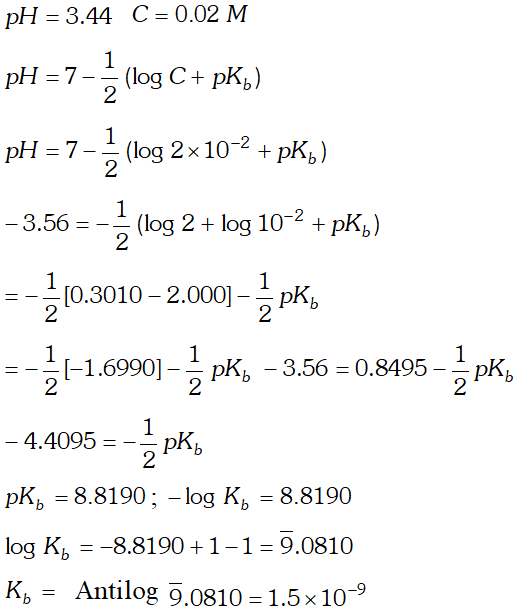
Q. The $p H$ of $0.005 M$ codeine $\left(\mathrm{C}_{18} \mathrm{H}_{21} \mathrm{NQ}_{3}\right)$ solution is 9.95 Calculate the ionization constant and $p K_{b}$
Ans. $\mathrm{Cod}+H_{2} \mathrm{O} \rightleftharpoons \mathrm{CodH}^{+}+\mathrm{OH}^{-}$ $p H=9.95 \therefore p O H=14-9.95=4.05$ i.e., $-\log \left[\mathrm{OH}^{-}\right]=4.05$ or $\log \left[O H^{-}\right]=-4.05=5.95$ or $\left[O H^{-}\right]=8.913 \times 10^{-5}$ $K_{b}=\frac{\left[\mathrm{Cod} H^{+}\right][\mathrm{OH}]}{[\mathrm{Cod}]}=\frac{[\mathrm{OH}]^{2}}{[\mathrm{Cod}}=\frac{\left(8.91 \times 10^{5}\right)^{2}}{5 \times 10^{-3}}=1.588 \times 10^{-6}$ $p K_{b}=-\log \left(1.588 \times 10^{-6}\right)=6-0.20=5.8$
Q. The ionization constant of HCOOH is $1.8 \times 10^{-4} .$ Around what $p H$ will its mixture with sodium formate gives buffer solution of higher capacity. Calculate the ratio of sodium formate \& formic acid in a buffer of $p H=4.25$
Ans. $p K_{a}=-\log K_{a}=-\log 1.8 \times 10^{-4}=3.74$ Buffer capacity is maximum near $p K_{a}$ of the acid $i . e .,$ at $p H=3.74 .$ In order to obtain a buffer solution of $p H=4.25$ we have $\log \frac{[\text { salt }]}{[\text { acid }]}=p H-p K_{a}=4.25-3.74=0.51$ $\frac{[\text { salt }]}{[\text { acid }]}=$ Antilog $0.51=3.24$ It means concentration of salt should be 3.24 times that of acid.
Q. The ionization constant of dimethylamine is $5.4 \times 10^{-4}$ Calculate the degree of ionization in its $0.02 M$ solution. What percentage of dimethylamine is ionized if the solution is also $0.1 M N a O H ?$
Ans. 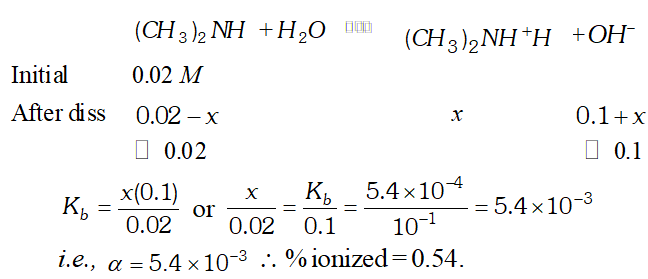
Q. The $p H$ of $0.1 M$ solution of cyanic acid (HCNO) is $2.34 .$ Calculate the ionization constant of the acid and its degree of ionization in the solution.
Ans. HCNO ionizes as: $H C N O=H^{+}+C N O^{-}$ The dissociation constant $K_{a}=\frac{\left[H^{+}\right][C N O]}{[H C N O]} \Rightarrow\left[H^{+}\right]=\left[C N O^{-}\right]$ Now, $p H=2.34$ $-\log \left[H^{+}\right]=2.34 \Rightarrow \log \left[H^{+}\right]=-2.34=3.36$ $\left(H^{+}\right)=$ Antilog $(3.36)=4.57 \times 10^{-3} \mathrm{M}$ $\therefore\left[H^{+}\right]=\left[C N O^{-}\right]=4.57 \times 10^{-3} M$ and $[H C N O]=0.1 M$ $K_{a}=\frac{\left(4.57 \times 10^{-3}\right) \times\left(4.57 \times 10^{-3}\right)}{0.1}=2.09 \times 10^{-4}$ Degree of dissociation $=\alpha=\sqrt{\frac{K_{a}}{c}}$ $=\sqrt{\frac{2.09 \times 10^{-4}}{0.1}}=4.57 \times 10^{-2} \mathrm{or}$
Q. The $p H$ of $0.004 M$ hydrazine solution is $9.7 .$ Calculate its ionization constant $K_{b}$ and $p K_{b}$
Ans. 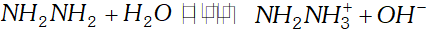
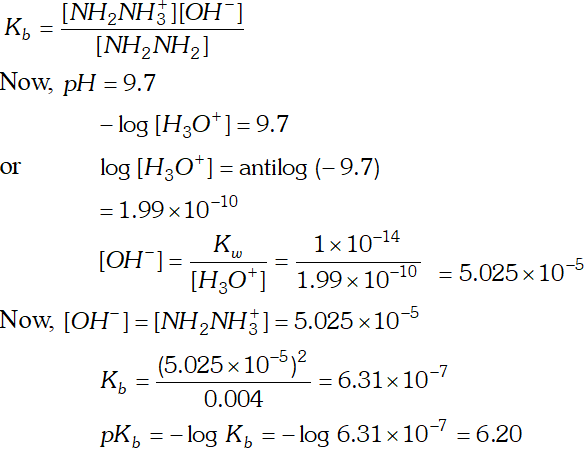
Q. Calculate the pH of the mixture formed by the addition of 5, 9, 9.5, 9.9, 9.95, 10, 10.05 and 10.1 mL of 0.5M KOH solution to 100 mL of 0.05 HBr solution. What will be the most suitable indicator for this titration ?
Ans. $5 m L$ of $0.5 M K O H=2.5$ millimoles $100 \mathrm{mL}$ of $0.05 \mathrm{M} \mathrm{HBr}=5$ milli moles $105 \mathrm{mL}$ of solution contains $5-2.5=2.5$ milli moles $=2.5 \times 10^{-3}$ moles of acid $1000 \mathrm{mL}$ of contains $=\frac{2.5 \times 10^{-3}}{105} \times 1000$ $=2.38 \times 10^{-2} \mathrm{mol} L^{-1}$ $p H=-\log 2.38 \times 10^{-2}=-\log 2.38-\log 10^{-2}$ $=-0.38+2.000=1.62$ Phenolpthalein and Thymolpt halein are suitable indicators.
Q. Benzoic acid is monobasic and when 1.22 g of its pure sample after dissolution in distilled water is titrated against a base it uses 50 mL of 0.2 M NaOH. Calculate the molar mass of benzoic acid.
Ans. $50 \mathrm{mL}$ of $0.2 \mathrm{MNaOH}=50 \times 0.2=10 \mathrm{millimoles}$ of $\mathrm{NaOH}$ 10 millimoles of $N a O H$ will neutralize 10 millimoles of Benzoic acid. 10 millimoles of benzoic acid $=1.22 \mathrm{g}$ 1 mole $=1000$ millimoles $=\frac{1.22}{10} \times 1000=122 \mathrm{g} \mathrm{mol}^{-1}$ Molecular weight $=122 \mathrm{g} \mathrm{mol}^{-1}$
Q. Equal volumes of $0.002 M$ solutions of sodium iodate and copper chlorate are mixed together. Will it lead to precipitation of copper iodate? For copper iodate $K_{s p}=7.4 \times 10^{-8}$
Ans. When equal volume of $\mathrm{NalO}_{3} \& \mathrm{CuClO}_{3}$ are mixed, the concentration of each of the solution will become half. $\left[\mathrm{IO}_{3}^{-}\right]=\frac{1}{2} \times 0.002=0.001=10^{-3}$ $\left[\mathrm{Cu}^{2+}\right]=\frac{1}{2} \times 0.002=0.001=10^{-3}$ $\mathrm{Cu}\left(\mathrm{IO}_{3}\right)_{2} \mathrm{H}$ tyth $\quad \mathrm{Cu}^{2+}+2 \mathrm{IO}_{3}^{-}$ I.P (Ionic product) $=\left[C u^{2+}\right]\left[I O_{3}^{-}\right]^{2}=\left[10^{-3}\right]\left[10^{-3}\right]^{2}=10^{-9}$ since $I . P .\left(1 \times 10^{-9}\right)$ is less than $K_{s p}\left(7.4 \times 10^{-8}\right),$ therefore No precipitation will take place.
Q. What is the maximum concentration of equimolar solutions of ferrous sulphate and sodium sulphide so that when mixed in equal volumes, therefore, is no precipitation of iron sulphide ? For iron sulphide $K_{s p}=6.3 \times 10^{-8}$
Ans. $K_{s p}=6.3 \times 10^{-8}$ FeS $\mathrm{HHH} \quad \mathrm{Fe}_{'^{\prime} \mathrm{S}}^{+2}+\mathrm{S}^{-2}$ $K_{s p}=6.3 \times 10^{-18}$ $K_{s p}=s \times s=s^{2}=6.3 \times 10^{-18}$ $s=2.51 \times 10^{-9}$ since volume of solution will become double on mixing equal volume of each solution. $\therefore$ concentration will become half on mixing max. concentration of each ion $=2 \times S$ $=2 \times 2.51 \times 10^{-9}=5.02 \times 10^{-9} \mathrm{m}$
Q. The ionization constant of phenol is $1.0 \times 10^{-10} .$ What is the concentration of phenate ion in $0.05 M$ solution of phenol? What will be its degree of ionization if the solution is also $0.01 M$ sodium phenate?
Ans. 
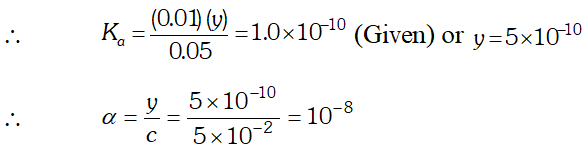
Q. The ionization constants of $H F, H C O O H$ and $H C N$ at $298 K$ are $6.8 \times 10^{4}, 1.8 \times 10^{4}$ and $4.8 \times 10^{9}$ respectively. Calculate the ionization constants of the corresponding conjugate base.
Ans. The relation between ionization constant of an acid and that of its conjugate base is $K_{a} \times K_{b}=K_{w}$ $\therefore \quad K_{b}=\frac{K_{w}}{K_{a}}$ The conjugate base of $H F$ is $F^{-}$ $K_{b\left(F^{-}\right)}=\frac{K_{w}}{K_{a}(H F)}=\frac{1 \times 10^{-14}}{6.8 \times 10^{-4}}=1.47 \times 10^{-11}$ The conjugate base of $H C O O H$ is $H C O O^{-}$ $K_{b}\left(H C O O^{-}\right)=\frac{K_{w}}{K_{a(H C O O H)}}=\frac{1 \times 10^{-14}}{1.8 \times 10^{-4}}=5.56 \times 10^{-11}$ The conjugate base of $H C N$ is $C N^{-}$ $K_{b\left(C N^{-}\right)}=\frac{K_{w}}{K_{a(H C N)}}=\frac{1 \times 10^{-14}}{4.8 \times 10^{-9}}=2.08 \times 10^{-6}$
Q. The ionization constant of $H F$ is $3.2 \times 10^{-4} .$ Calculate the degree of dissociation of $H F$ in its $0.02 M$ solution. Calculate the concentration of all species present $\left(H_{3} O^{4}, F^{-} \text {andHH } \text { in the solution and its } p H\right.$
Ans. If $C$ is the initial concentration and $\alpha$ is the degree of ionization of $H F$ then

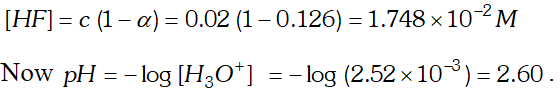
Q. The $p H$ of a $0.01 M$ solution of an organic acid is 4.15 Calculate (i) the concentration of the anion (ii) ionization constant of the acid (iii) $\quad p K_{a}$
Ans. $p H=4.15$ $-\log \left[H_{3} O^{+}\right]=4.15$ or $\log \left[H_{3} O^{+}\right]=-4.15=\overline{5} .85$ $\therefore \log \left[H_{3} O^{+}\right]=$ antilog $(\overline{5} .85)=7.08 \times 10^{-5}$ $\mathrm{Now},\left[H_{3} \mathrm{O}^{+}\right]=\left[A^{-}\right]=7.08 \times 10^{-5} \mathrm{M}$ (i) Concentration of anion $=7.08 \times 10^{-5} \mathrm{M}$ (ii) Ionization constant of acid $H A(a q)+H_{2} O(l) ! H_{3} O^{+}(a q)+A^{-}(a q)$ \[ K_{a}=\frac{\left[H_{3} O^{+}\right]\left[A^{-}\right]}{[H A]} \] Concentration of undissociated acid $=0.01-0.000078$ $=0.009922$ $\therefore K_{a}=\frac{\left(7.08 \times 10^{-5}\right) \times\left(7.08 \times 10^{-5}\right)}{0.009922}=5.05 \times 10^{-7}$ (iii) \[ p K_{a}=-\log K_{a}=-\left(5.05 \times 10^{-7}\right)=6.30 \]
Q. Calculate the degree of ionization and $p H$ of $0.05 M$ ammonia solution. The ionization constant of ammonia $\left(K_{b}\right)$ is $1.77 \times 10^{-5} .$ Also calculate the ionic constant of the conjugate acid of ammonia.
Ans. 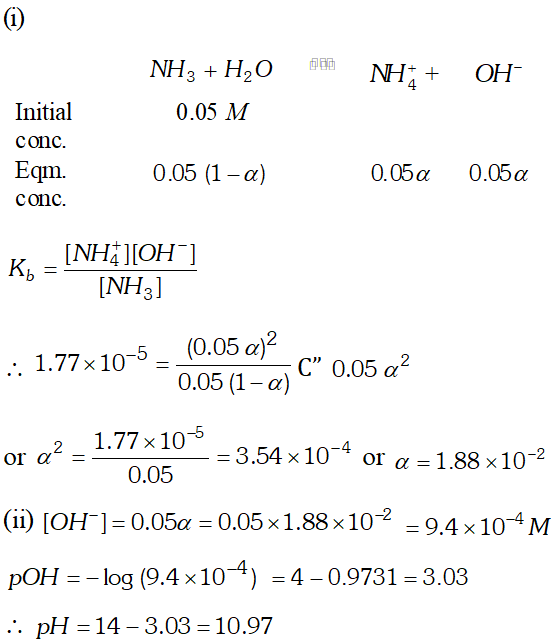
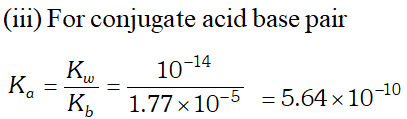
Q. The ionization constant of benzoic acid is $6.46 \times 10^{-5}$ and $K_{s p}$ for silver benzoate is $2.5 \times 10^{-13} .$ How many times is silver benzoate more soluble in a buffer of $p H$ 3.19 compared to its solubility in pure water?
Ans. 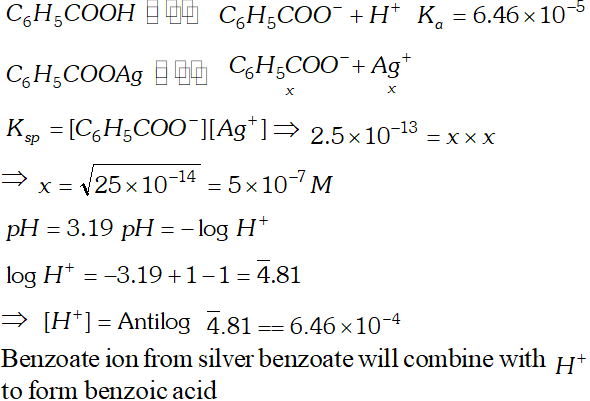
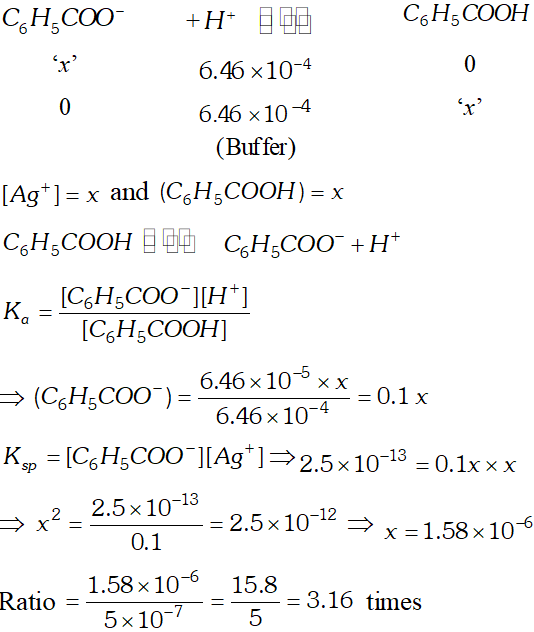 Silver benzoate is 3.16 times more souble in buffer solution of $p H=3.19$ than in pure water.
Silver benzoate is 3.16 times more souble in buffer solution of $p H=3.19$ than in pure water. Q. The indicators will be suitable for the following acid $-$ base titration? (i) $\mathrm{HCOOH}$ against $\mathrm{NaOH}$ (ii) $\mathrm{HBr}$ against $K O H$ (iii) $N H_{4} O H$ against $H N O_{3} .$
Ans. (i) Phenolpthalein (ii) Phenolpthalein (iii) Methyl orange
Q. (i) Write the conjugate acids for the following Bronsted \[ \text { bases: } \mathrm{NH}_{2}^{-}, \mathrm{NH}_{3} \text { and } \mathrm{HCOO}^{-} \] (ii) Write the conjugate bases for the following \[ \text { Bronsted acids: } H F, H_{2} S O_{4}, H C O_{3}^{-} \]
Ans. (1) Conjugate acids (a) $\mathrm{NH}_{2}^{-}: \mathrm{NH}_{3}$ (b) $N H_{3}: \mathrm{NH}_{4}^{+}$ (c) $\mathrm{HCOO}^{-}: \mathrm{HCOOH}$ (ii) Conjugate bases \[ \begin{array}{l} {H F: F^{-}} \\ {H_{2} S O_{4}: H S O_{4}^{-}} \\ {H C O_{3}^{-}: C O_{3}^{2-}} \end{array} \]
Q. The species $H_{2} \mathrm{O}, \mathrm{HCO}_{3}^{-}, \mathrm{HSO}_{4}^{-}$ and $\mathrm{NH}_{3}$ can act both as Bronsted acids and bases. Give the corresponding conjugate acid and base.
Ans. 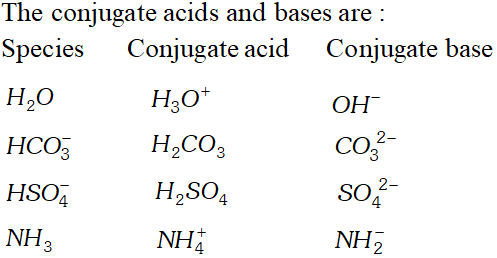
Q. Classify the following species into Lewis acids and Lewis bases and show how these act as such: $\begin{array}{llll}{\text { (i) } H O^{-}} & {\text {(ii) } F^{-}} & {\text {(iii) } H^{+}} & {\text {(iv) } B C l_{3}}\end{array}$
Ans. (i) $\mathrm{HO}^{-}$ is a Lewis base because it can donate a pair of electrons. (ii) $F^{-}$ acts as a Lewis base because it can donate a pair of electron. (iii) $H^{+}$ is a Lewis acid because it can accept a lone pair of electrons from base like $\mathrm{OH}^{-}$ and ions. a (iv) acts as a Lewis acid because it is electron deficient and can accept a lone pair of electrons.
Q. What is meant by the conjugate acid base pair? Find the conjugate acid/base for the following compounds and ions: $H N O_{2}, C N^{-}, H C l O_{4}, F^{-}, O H^{-}, C O_{3}^{2-}$ and $S^{2-}$
Ans. Acid can donate a proton to form base, which is called conjugate base of that acid. Base can accept a proton to form acid, which is called conjugate acid of that base, e.g.
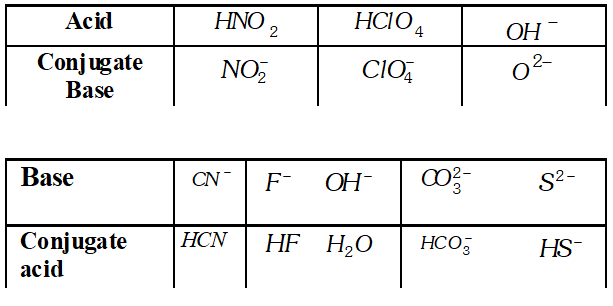
Q. Assuming complete dissociation calculate the $p H$ of the following solution: $0.003 M H C l,(\text { ii }) 0.005 M N a O H,$ (iii) $0.002 M H B r$ (iv) $0.002 M K O H$
Ans. 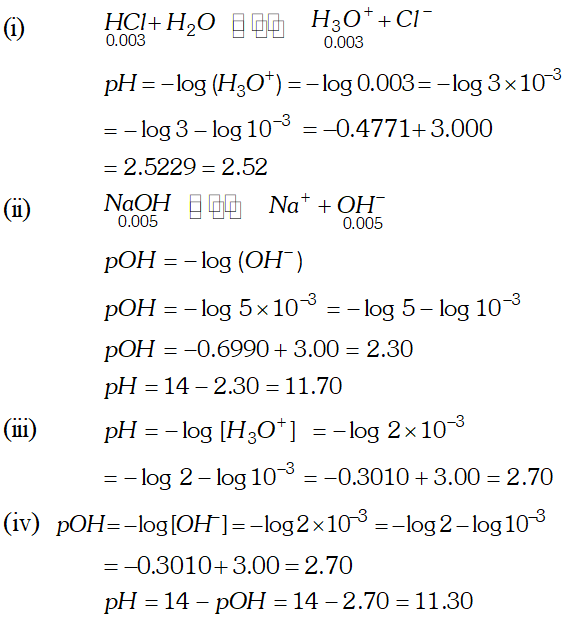
Q. If $0.56 g K O H$ is dissolved in water to give $200 \mathrm{mL}$ of solution at $298 \mathrm{K}$ Calculate the concentration of potassium, hydrogen and hydroxyl ions. What is its $p H ?$
Ans. 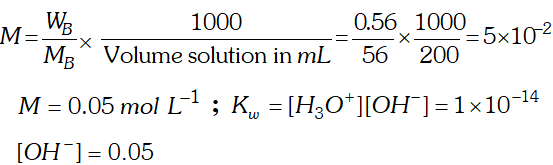
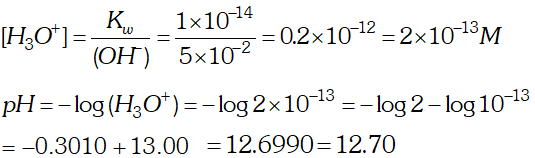
Q. The solubility of $\operatorname{Sr}(\mathrm{OH})_{2}$ at $298 \mathrm{K}$ is $19.23 \mathrm{g} / \mathrm{L}$ of solution. Calculate the concentration of strontium and hydroxyl ions and the $p H$ of the solution.
Ans. 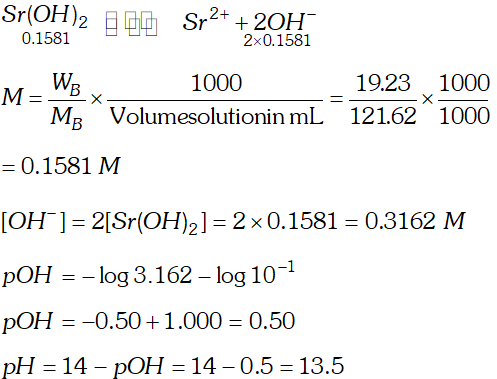
Q. Calculate the $p H$ of $0.05 M$ sodium acetate solution if the $p K_{a}$ of acetic acid is 4.74
Ans. 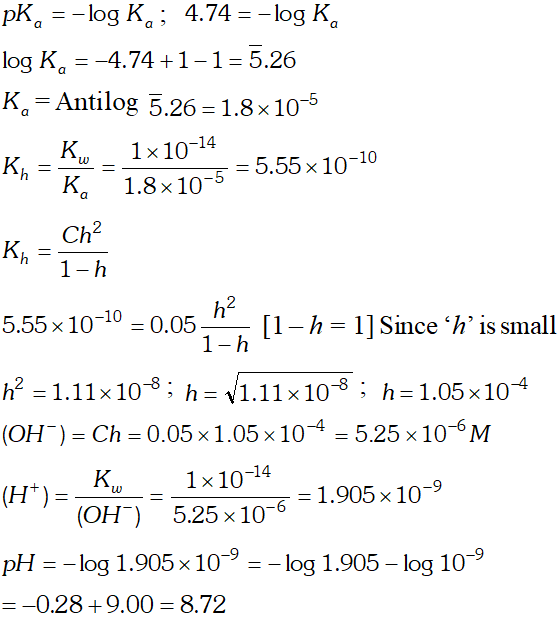
Q. A solution gives the following colour with different indicators methyl orange-yellow, methyl red-yellow, bromothymol blue-orange. What is approximate pH of the solution? Explain giving reason.
Ans. The colour in methyl orange indicates that $p H>4.5$ The colour in methyl red indicates that $p H>6.0$ The colour in bromothymol blue indicates that $p H<6.3$ Therefore, $p H$ of the solution is between 6.0 to 6.3
Q. The colour in methyl orange indicates that $p H>4.5$ The colour in methyl red indicates that $p H>6.0$ The colour in bromothymol blue indicates that $p H<6.3$ Therefore, $p H$ of the solution is between 6.0 to 6.3
Ans. 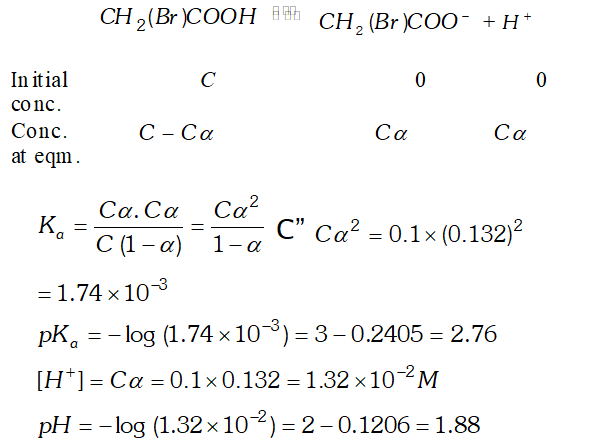
Q. The ionization constant of nitrous acid is $4.5 \times 10^{-4}$ Calculate the $p H$ of $0.04 M$ sodium nitrite solution and also its degree of hydrolysis.
Ans. Sodium nitrite is a salt of strong base and weak acid. Its degree of hydrolysis,
h is given by the relation :
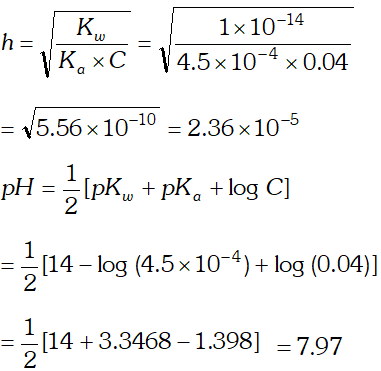
Q. The ionization constant of the $\mathrm{CH}_{3} \mathrm{COOH}$ is $1.74 \times 10^{-5} .$ Calculate the degree of the dissociation of acetic acid in its $0.05 \mathrm{M}$ solution. Calculate the concentration of the $\mathrm{CH}_{3} \mathrm{COO}^{-}$ and its $p H$
Q. $p H$ of $0.01 M$ of an organic acid is $4.15 .$ Calculate the concentration of the anion and $K_{a} \&$ its $p K_{a}$
Ans. 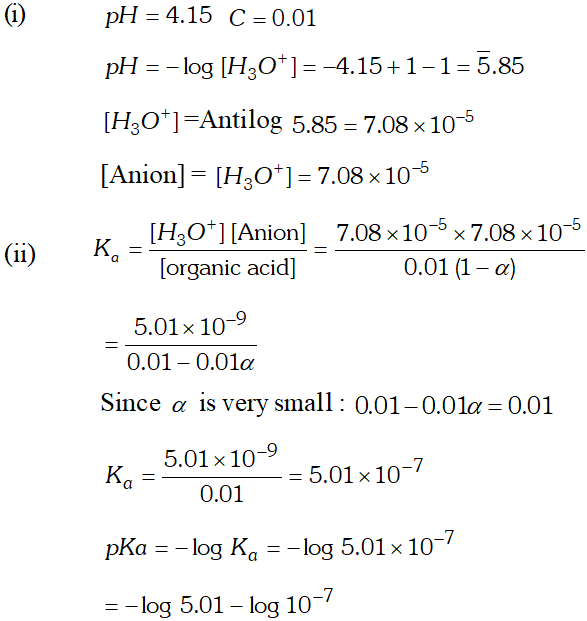
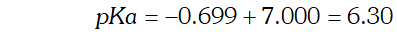
Q. How much volume of $0.1 \mathrm{MCH}_{3} \mathrm{COOH}[\mathrm{HAc}]$ should be added to $50 \mathrm{mL}$ of $0.2 \mathrm{M}$ NaAc (sodium acetate) solution if we want to prepare a buffer solution of $p H=4.91$
Ans. 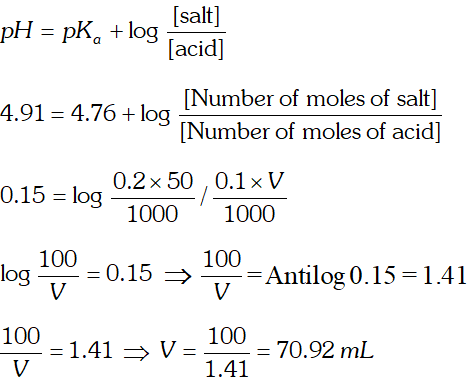
Q. How much of $0.3 \mathrm{M} \mathrm{NH}_{4} \mathrm{OH}$ should be mixed with $30 \mathrm{ml}$ of $0.2 M N H_{4} C l$ to give buffer solution of $p H 8.65$ to 10 $\left(p K_{b} \text { of } N H_{4}^{\pm}=4.75\right)$
Ans. $p K_{a}$ for $N H_{4}^{+}=14-4.75=9.25 \quad\left[\because p K_{b}=4.75\right]$ $p H=p K_{a}+\log \frac{N H_{4} O H}{\left[N H_{4}^{+}\right]}$ $8.65=9.25+\log \frac{\left[N H_{4} O H\right]}{\left[N H_{4}^{+}\right]}$ $\log \frac{\left[N H_{4} O H\right]}{\left[N H_{4} C l\right]}=-0.60+1-1=\overline{1} .40$ $\frac{\left[N H_{4} O H\right]}{\left[N H_{4} C l\right]}=$ antilog $\overline{1} .40=0.25$ $\frac{\left[N H_{4} O H\right]}{\left[N H_{4} C l\right]}=\frac{0.3 \times V / 1000}{0.2 \times 30 / 1000}=0.25$ $V=5.00 \mathrm{mL}$ for $p H=10$ $10=9.25+\log \frac{\left[N H_{4} O H\right]}{\left[N H_{4} C l\right]}=0.75=\log \frac{\left[N H_{4} O H\right]}{\left[N H_{4} C l\right]}$ $\log \frac{\left[N H_{4} O H\right]}{\left[N H_{4} C l\right]}=0.75 ; \frac{\left[N H_{4} O H\right]}{\left[N H_{4} C l\right]}=5.8$ $\frac{0.3 \times V / 1000}{0.2 \times 30 / 1000}=5.8, V=20 \times 5.8=116 \mathrm{mL}$
Q. The ionization constant of acetic acid is $1.74 \times 10^{-5}$ Calculate the degree of dissociation of acetic acid in its $0.05 M$ solution. Calculate the concentration of acetate ion in the solution and its $p H ?$
Ans. 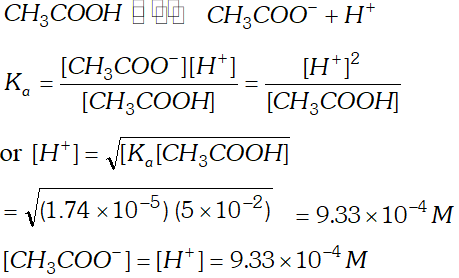 $p H=-\log \left(9.33 \times 10^{-4}\right)=4-0.9699=4-0.97=3.03$
$p H=-\log \left(9.33 \times 10^{-4}\right)=4-0.9699=4-0.97=3.03$ Q. $100 \mathrm{mL}$ of $\frac{N}{10} \mathrm{NaOH}$ solution is mixed with $100 \mathrm{mL}$ of $\frac{N}{5} H C l$ solution and the whole solution is made up to 1 litre. What is the $p H$ of resulting solution?
Ans. Number of meq of $\mathrm{NaOH}=100 \times \frac{1}{10}=10 \mathrm{meq}$ Number of meq of $H C l=100 \times \frac{1}{5}=20$ meq No. of meq of $H C l$ in $200 \mathrm{mL}$ solution on mixing $=10 \mathrm{meq}$ $200 m L$ of solution contains $10 \mathrm{meq}$ $=10 \times 10^{-3} e q=10 \times 10^{-3} \mathrm{moles}$ of $\mathrm{HCl}$ $=\frac{10^{-2}}{200} \times 1000=5 \times 10^{-2} \mathrm{mol} L^{-1}$ of $H C l$ $p H=-\log \left[H_{3} O^{+}\right]=-\log 5 \times 10^{-2}=-\log 5-\log 10^{-2}$ $=-0.6990+2.000=1.3010$
Q. Ionic product of water at $310 K$ is $2.7 \times 10^{-14} .$ What is the neutral $p H$ of water at this temperature?
Ans. $K_{w}=2.7 \times 10^{-14}$ $K_{w}=\left[H_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=2.7 \times 10^{-14}$ $\left[H_{3} O^{+}\right]=\left[O H^{-}\right] ;\left[H_{3} O^{+}\right]^{2}=2.7 \times 10^{-14}$ $\left[H_{3} O^{+}\right]=\sqrt{2.7} \times 10^{-7} ;\left[H_{3} O^{+}\right]=1.65 \times 10^{-7}$ $\left[H_{3} O^{+}\right]=1.65 \times 10^{-7}$ $p H=-\log 1.65 \times 10^{-7}=-\log 1.65-\log 10^{-7}$ $=-0.217+7.000=6.78$
Q. $K_{b}$ for $N H_{4} O H$ is $1.77 \times 10^{-5}$ at $298 K .$ calculate the hydrolysis constant of $N H_{4} C l$ and $p H$ of $0.04 M N H_{4} C l$ solution.
Ans. 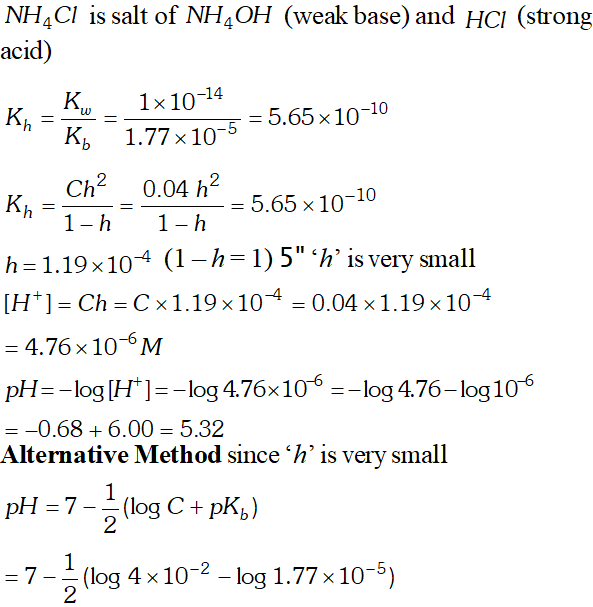
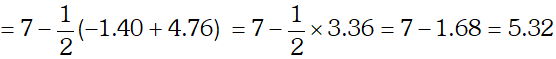
Q. The degree of ionization of a $0.1 M$ bromo acetic acid solution is $0.132 .$ Calculate the $p H$ of solution and the $p K_{a}$ of bromo acetic acid.
Ans. Degree of dissociation, $\alpha=0.132$ Concentration of $H_{3} \mathrm{O}^{+}$ ion $\left[H_{3} O^{+}\right]=c, \alpha=0.1 \times 0.132=0.0132 M$ $p H=-\log \left[H_{3} O^{+}\right]$ $=-\log (0.0132)=-(-1.88)=1.88$ The dissociation constant, $K_{a}=\frac{c \alpha^{2}}{1-\alpha}=\frac{0.1 \times(0.132)^{2}}{1-0.132}=2.01 \times 10^{-3}$ $p K_{a}=-\log K_{a}=-\log \left(2.01 \times 10^{-3}\right)=-0.303+3=2.7$
Q. The $p K_{b}$ of acetic acid and $p K_{a}$ of $N H_{4} O H$ are 4.76 and 4.75 respectively. Calculate the $K_{h}$ of $\mathrm{CH}_{3} \mathrm{COONH}_{4}$ at $298 K$ also the degree of the hydrolysis and $p H$ of its (a) $0.01 \mathrm{Mand}$ (b) $0.04 \mathrm{M}$
Ans. 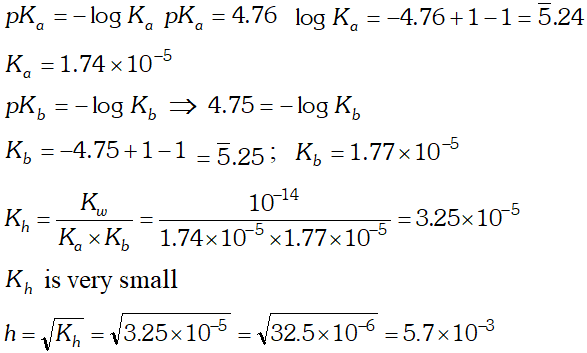
Q. Calculate the degree of hydrolysis and $p H$ of $0.02 M$ $N H_{4} C N$ solution at $298 K . K_{b}$ for $N H_{4} O H=1.77 \times 10^{5} K_{a}$ for $H C N=4.99 \times 10^{-10}$
Ans. 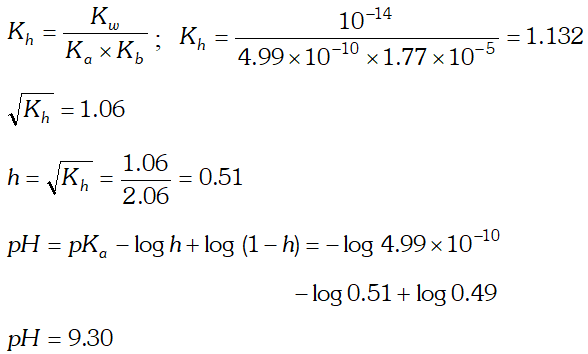
Q. (i) Define ionic equilibrium giving an example. (ii) For the reaction $\left[A g(C N)_{2}\right]^{-}$ E $\mathbb{E} \mathbb{Z} \quad A g^{+}+2 C N^{-}$ $K=4.0 \times 10^{-19}$ at $25^{\circ} \mathrm{C} .$ Calculate the silver ion concentration in a solution which was originally $0.10 M$ in $K C N$ and $0.03 M$ in $A g N O_{3}$
Ans. 
Q. What is the $p H$ of $0.001 M$ aniline solution? The ionization constant of aniline is $4.27 \times 10^{-10} .$ Calculate the degree of ionization of aniline in the solution. Also calculate the ionization constant of the conjugate acid of aniline.
Ans. 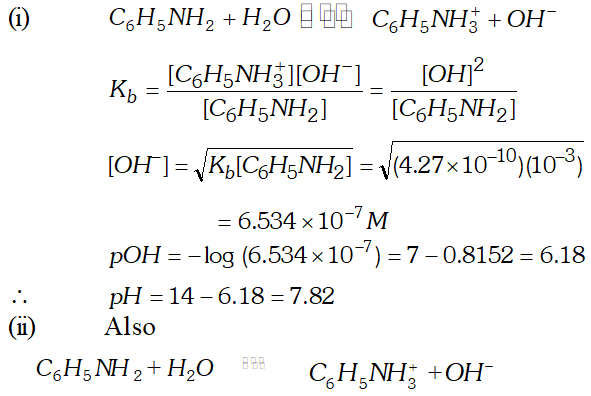
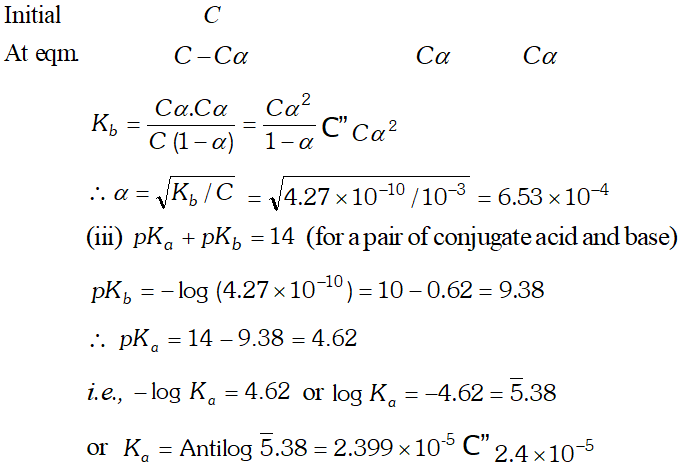
Q. Calculate the solubility of $A g C l, F e(O H)_{3}, A g_{2} S O_{4}$ and $H g_{2} B r_{2} \quad$ from $\quad$ their solubility products. $K_{s p}(A g C l)=1.8 \times 10^{-10}, \quad K_{s p}\left[F e(O H)_{3}\right]=1.0 \times 10^{-38}$ $K_{s p}\left[A g_{2} S O_{4}\right]=1.4 \times 10^{-5}, \quad K_{s p}\left(H g_{2} B r_{2}\right)=5.6 \times 10^{-23}$ Also calculate the solubilities of salts in $g L^{-1}$ and molarities of the ions.
Q. Determine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at $298 \mathrm{K.~Given~} K_{s p}$ values: $A g_{2} C r O_{4}=1.1 \times 10^{-12}, B a C r O_{4}=1.2 \times 10^{-10}, F e(O H)_{3}$ $=1.0 \times 10^{-38}$ $P b C l_{2}=1.6 \times 10^{-5}, H g_{2} I_{2}=4.5 \times 10^{-29}$ Determine also the molarities of individual ions.
Ans. 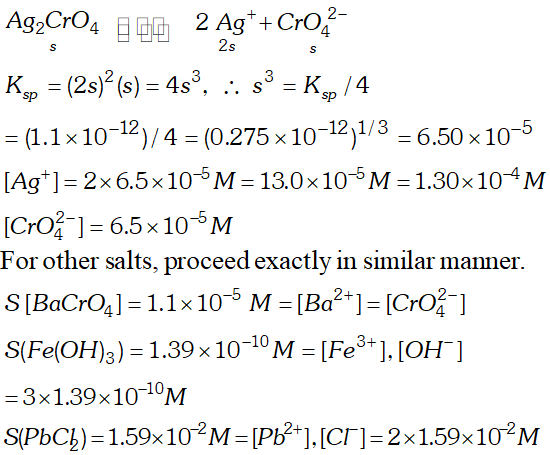
Q. (i) State the formula of conjugate base of each of the following acids: (a) $H_{3} \mathrm{O}^{-}$ (b) $\mathrm{HSO}_{4}^{-}$ (c) $H_{3} P O_{4}$ (d) $\mathrm{CH}_{3} \mathrm{N}^{+} \mathrm{H}_{3}$ (ii) State the formula of conjugate acid of the following (a) $\mathrm{OH}^{-}$ (b) $\mathrm{CO}_{3}^{2-}$ (c) $\left(\mathrm{CH}_{3}\right)_{2} \mathrm{NH}$ (d) $\mathrm{HPO}_{4}^{2-}$ (iii) Arranging the following in increasing order of basic IT ; $\left.F^{-}, B r^{-}, C l^{-}, I^{-} .\right]$
Ans. (i) $(\mathrm{a}) \mathrm{H}_{2} \mathrm{O},(\mathrm{b}) \mathrm{SO}_{4}^{2-},(\mathrm{c}) \mathrm{H}_{2} \mathrm{PO}_{4}^{-},(\mathrm{d}) \mathrm{CH}_{3} \mathrm{NH}_{2}$ (ii) $(\mathrm{a}) \mathrm{H}_{2} \mathrm{O},(\mathrm{b}) \mathrm{HCO}_{3}^{-},(\mathrm{c})\left(\mathrm{CH}_{3}\right)_{2} \mathrm{NH}_{2},(\mathrm{d})$ (iii) $F^{-}>C l^{-}>B r^{-}>I^{-}$
Q. The first ionization constant of $H_{2} S$ is $9.1 \times 10^{-8} .$ Calculate the concentration of $H S^{-}$ ion is its $0.1 M$ solution. How will this concentration be effected if the solution is $0.1 M H C l$ also. If the second dissociation constant of $H_{2} S$ is $1.2 \times 10^{-13}$, calculate the concentration of $S^{-2}$ ion under these conditions.
Q. (i) Calculate $p H$ of an aqueous solution of $1.0 \mathrm{M}$ ammonium formate assuming complete dissociation. $\left(p K_{a} \text { of } H C O O H=3.8 \text { and } p K_{b} \text { of } N H_{3}=4.8\right)$ (ii) Saccharine $\left(K_{a}=2 \times 10^{-12}\right)$ is a weak acid represented by formula Hsac. $4 \times 10^{-4} \mathrm{mol}$ of saccharine is dissolved in $200 \mathrm{cm}^{3}$ water $p H=3 .$ Assuming no change in volume, calculate the concentration of $S a c^{-}$ ion in resulting solution.
Ans. 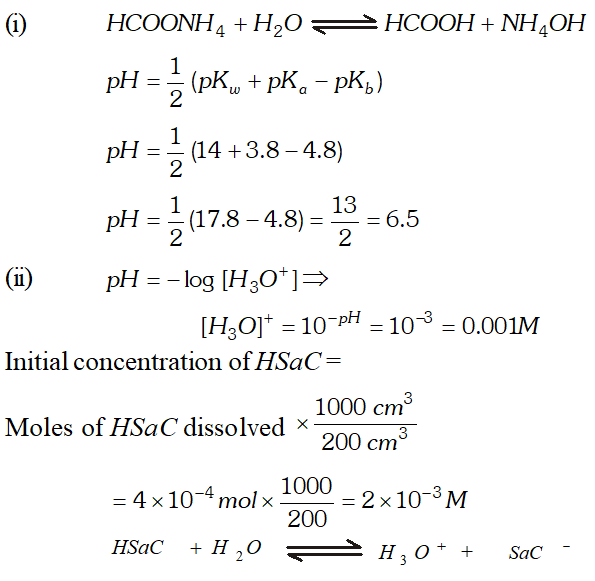
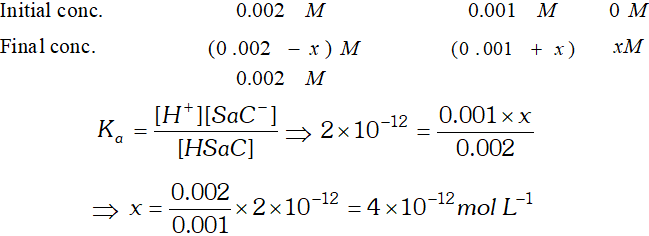
![]()
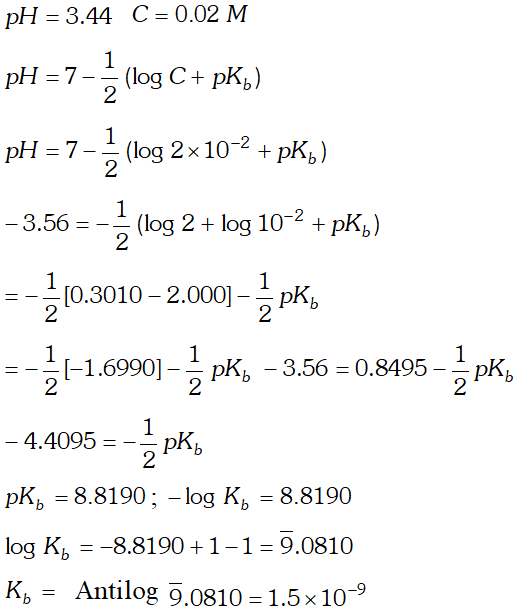
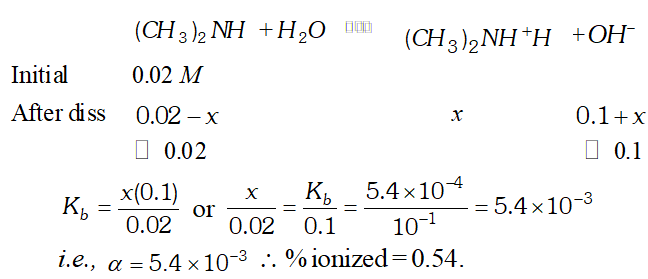
![]()
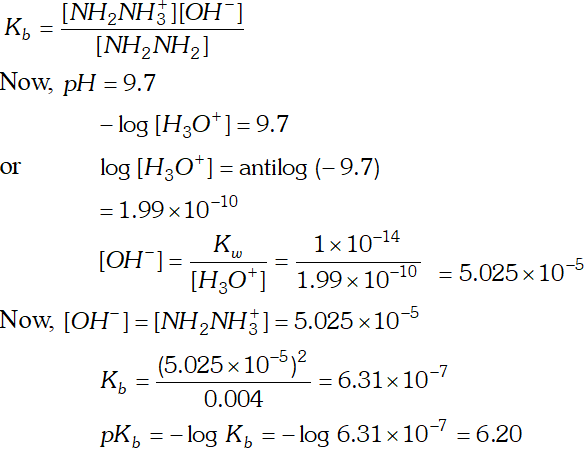

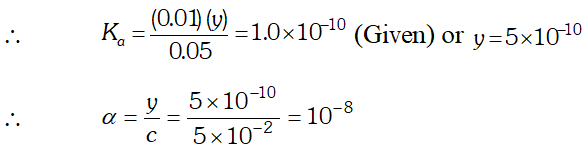

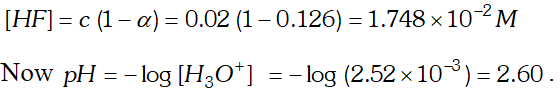
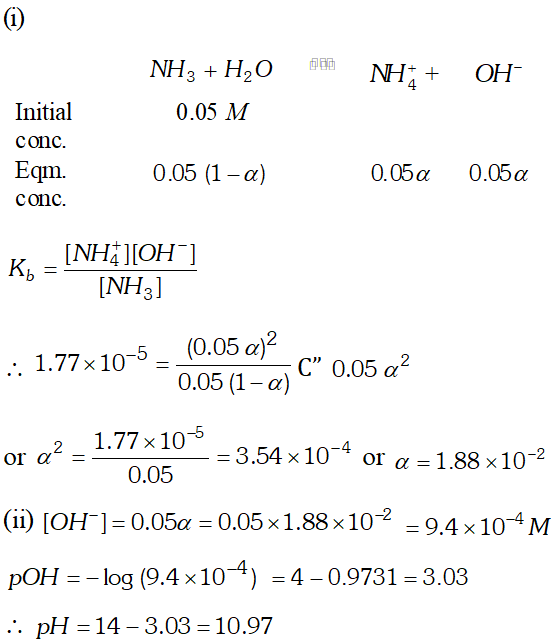
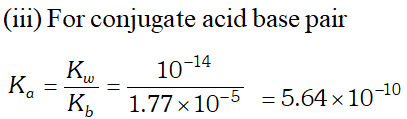
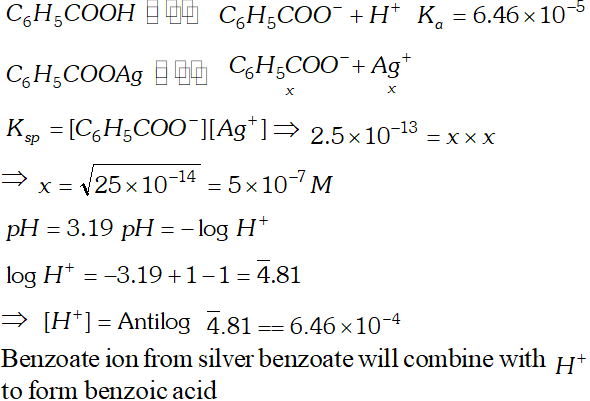
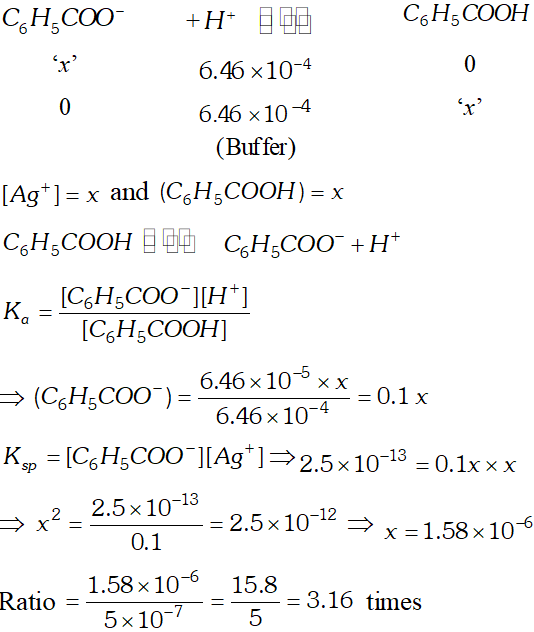 Silver benzoate is 3.16 times more souble in buffer solution of $p H=3.19$ than in pure water.
Silver benzoate is 3.16 times more souble in buffer solution of $p H=3.19$ than in pure water. 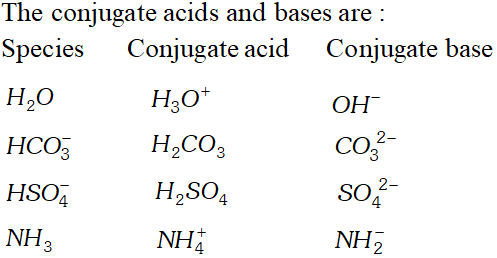

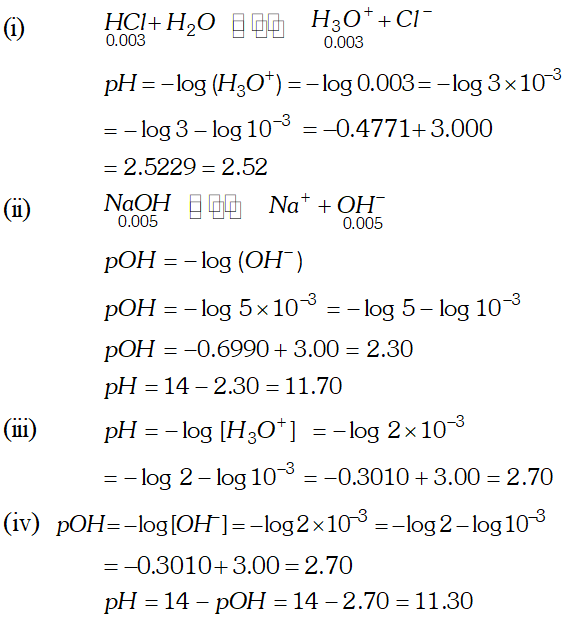
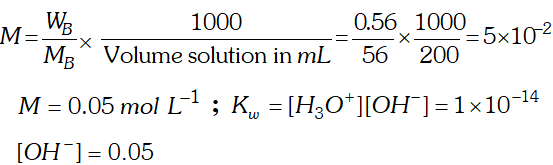
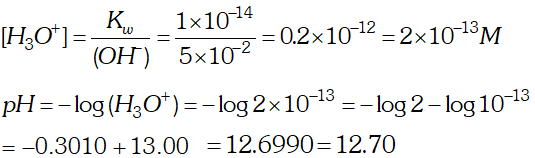
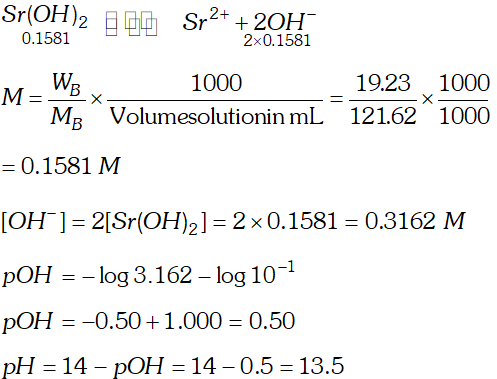
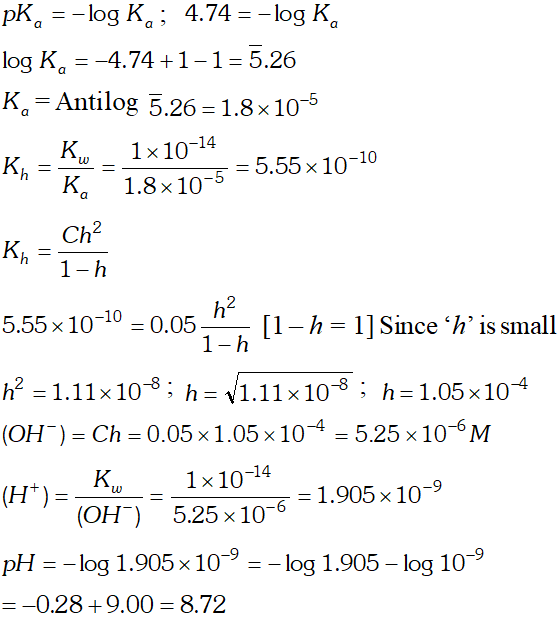
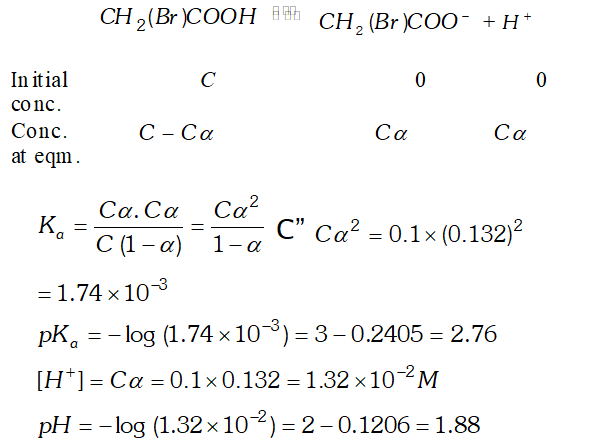
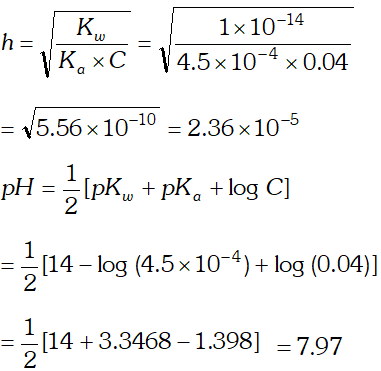
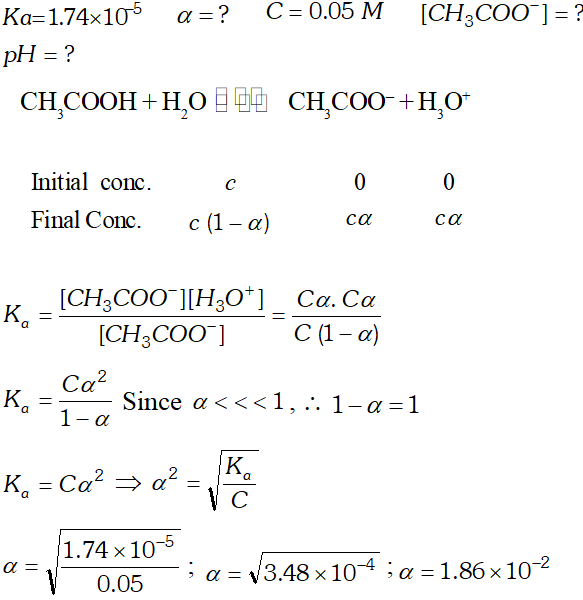
![]()
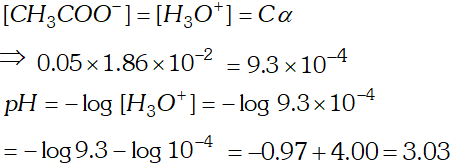
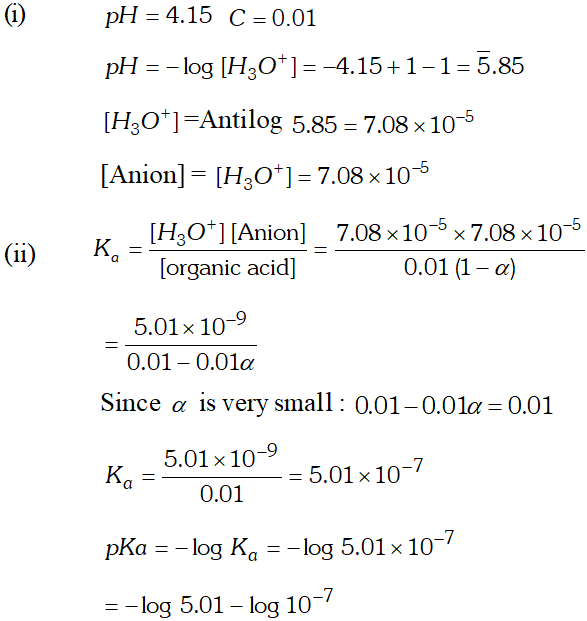
![]()
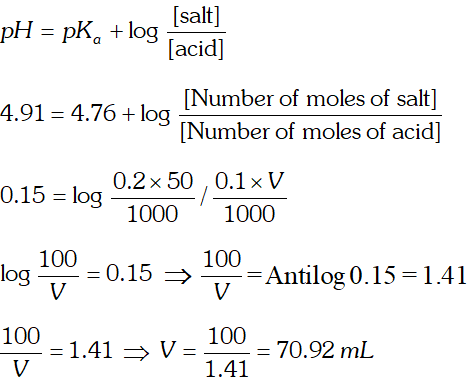
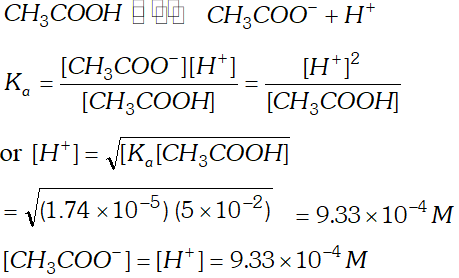 $p H=-\log \left(9.33 \times 10^{-4}\right)=4-0.9699=4-0.97=3.03$
$p H=-\log \left(9.33 \times 10^{-4}\right)=4-0.9699=4-0.97=3.03$ 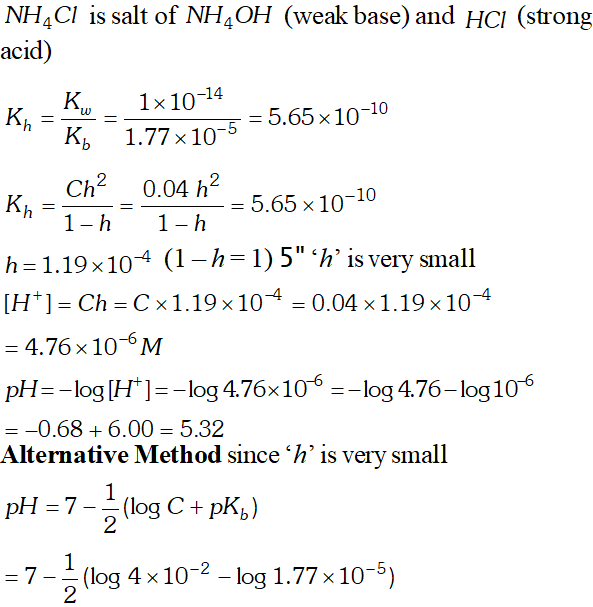
![]()