The magnetic field due to a short bar magnet at any point on the axial line is twice the magnetic field at a point on the equatorial line of that magnet at the same distance. S.l. unit of torque acting on the bar magnet is Nm.
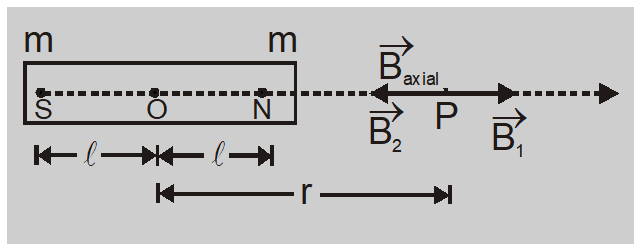
$\overrightarrow{ B }_{\text {axial }}=\overrightarrow{ B _{1}}+\overrightarrow{ B _{2}}$
$\overrightarrow{ B }_{1}=\frac{\mu_{0}}{4 \pi} \frac{ m }{( r -\ell)^{2}}(\hat{ r })$ and $\overrightarrow{ B }_{2}=\frac{\mu_{0}}{4 \pi} \frac{ m }{( r +\ell)^{2}}(-\hat{ r })$
$\therefore \quad \vec{B}_{\text {axal }}=\left[\frac{\mu_{0}}{4 \pi} \frac{m}{(r-\ell)^{2}}-\frac{\mu_{0}}{4 \pi} \frac{m}{(r+\ell)^{2}}\right]$
$\hat{\mathrm{r}}=\frac{\mu_{0} \mathrm{~m}}{4 \pi}\left[\frac{4 \mathrm{r} \ell}{(\mathrm{r}-\ell)^{2}(\mathrm{r}+\ell)^{2}}\right] \hat{\mathrm{r}}$
$\overrightarrow{ B }_{ axial }=\frac{\mu_{0}}{4 \pi} \frac{2 \overrightarrow{ Mr }}{\left( r ^{2}-\ell^{2}\right)^{2}}$
Magnetic field due to a bar magnet at an axial point has same direction as that of its magnetic dipole moment vector.
For a bar magnet of very small length $\ell<< r \overrightarrow{ B }_{ axial }=\frac{\mu_{0}}{4 \pi} \frac{2 \overrightarrow{ M }}{r^{3}}$
Browse More Topics Related Magnetism:
$\left|\overrightarrow{ B }_{1}\right|=\frac{\mu_{0}}{4 \pi} \frac{ m }{ NP ^{2}}=\frac{\mu_{0}}{4 \pi} \frac{ m }{ r ^{2}+\ell^{2}}$ along $NP$
$\left|\overrightarrow{ B }_{2}\right|=\frac{\mu_{0}}{4 \pi} \frac{ m }{ SP ^{2}}=\frac{\mu_{0}}{4 \pi} \frac{ m }{\left( r ^{2}+\ell^{2}\right)}$ along $PS$
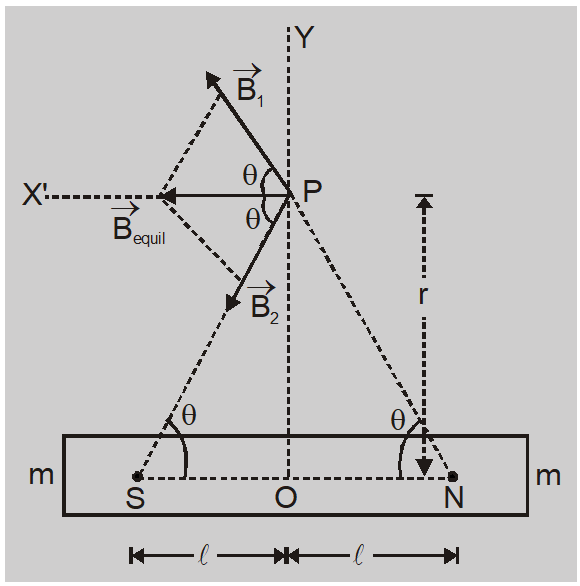
So $\left|\vec{B}_{1}\right|=\left|\vec{B}_{2}\right|$ On resolving $\vec{B}_{1}$ and $\overrightarrow{ B _{2}}$ along PX' and PY we find $\left|\vec{B}_{1}\right|$ $\sin \theta$ and $|\overrightarrow {{B_2}} |\,\sin \theta $
are equal and opposite so they cancel each other. So resultant field
$\overrightarrow{\mathrm{B}}_{\text {equi }}=\overrightarrow{\mathrm{B}}_{1} \cos \theta(-\hat{\mathrm{r}})+\overrightarrow{\mathrm{B}}_{2} \cos \theta(-\hat{\mathrm{r}})$
$=\left[\frac{\mu_{0}}{4 \pi} \frac{m}{\left(r^{2}+\ell^{2}\right)} \cos \theta+\frac{\mu_{0}}{4 \pi} \frac{m}{\left(r^{2}+\ell^{2}\right)} \cos \theta\right](-\hat{r})$
$=2 \cdot \frac{\mu_{0}}{4 \pi} \frac{ m }{\left( r ^{2}+\ell^{2}\right)} \cdot \frac{\ell}{\sqrt{ r ^{2}+\ell^{2}}}(-\hat{ r })$
$\overrightarrow{ B }_{ equi }=-\frac{\mu_{0}}{4 \pi} \frac{\overrightarrow{ M }}{\left( r ^{2}+\ell^{2}\right)^{\frac{3}{2}}}$
$\overrightarrow{ B }_{ equi }=-\frac{\mu_{0}}{4 \pi} \frac{\overrightarrow{ M }}{\left( r ^{2}+\ell^{2}\right)^{\frac{3}{2}}}$
The direction of magnetic field at a point on equitorial line is opposite to magnetic dipole moment vector.
For a bar magnet of very small length $\overrightarrow{ B }_{ equi }=-\frac{\mu_{0}}{4 \pi} \frac{\overrightarrow{ M }}{r^{3}}$
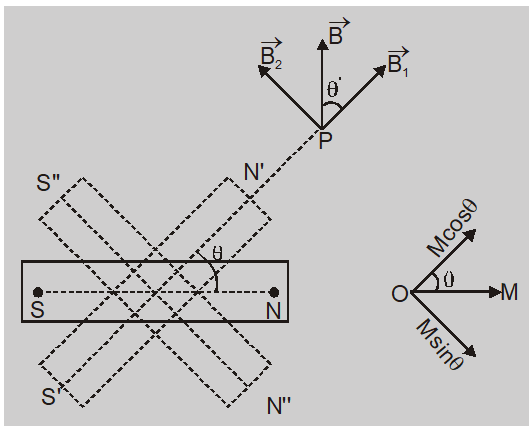
The point P is simultaneously on the equatorial line of other magnet N"S" with magnetic moment Msin $\theta $ Magnetic flux density $B _{2}=\frac{\mu_{0}}{4 \pi} \frac{ M \sin \theta}{ r ^{3}}$
Total magnetic flux density at P.
$B =\sqrt{ B _{1}^{2}+ B _{2}^{2}}=\frac{\mu_{0}}{4 \pi} \frac{ M }{ r ^{3}} \sqrt{4 \cos ^{2} \theta+\sin ^{2} \theta}$ or
$\tan \theta^{\prime}=\frac{B_{2}}{B_{1}}=\frac{\frac{\mu_{0}}{4 \pi} \frac{M \sin \theta}{r^{3}}}{\frac{\mu_{0}}{4 \pi} \frac{2 M \cos \theta}{r^{3}}}=\frac{1}{2} \tan \theta$ or $\theta^{\prime}=\tan ^{-1}\left(\frac{1}{2} \tan \theta\right)$
Click here for the Video tutorials of Magnetic Effect of Current Class 12
Magnetic field due to a short bar magnet (magnetic dipole) :
On Axial Point or End on Position
The magnetic field $\overrightarrow{ B }_{\text {axial }}$ at a point P due to bar magnet will be the resultant of the magnetic fields $\overrightarrow{ B _{1}}$ due to N-pole of magnet and $\overrightarrow{ B _{2}}$ due to S-pole of magnet.
$\overrightarrow{ B }_{\text {axial }}=\overrightarrow{ B _{1}}+\overrightarrow{ B _{2}}$
$\overrightarrow{ B }_{1}=\frac{\mu_{0}}{4 \pi} \frac{ m }{( r -\ell)^{2}}(\hat{ r })$ and $\overrightarrow{ B }_{2}=\frac{\mu_{0}}{4 \pi} \frac{ m }{( r +\ell)^{2}}(-\hat{ r })$
$\therefore \quad \vec{B}_{\text {axal }}=\left[\frac{\mu_{0}}{4 \pi} \frac{m}{(r-\ell)^{2}}-\frac{\mu_{0}}{4 \pi} \frac{m}{(r+\ell)^{2}}\right]$
$\hat{\mathrm{r}}=\frac{\mu_{0} \mathrm{~m}}{4 \pi}\left[\frac{4 \mathrm{r} \ell}{(\mathrm{r}-\ell)^{2}(\mathrm{r}+\ell)^{2}}\right] \hat{\mathrm{r}}$
$\overrightarrow{ B }_{ axial }=\frac{\mu_{0}}{4 \pi} \frac{2 \overrightarrow{ Mr }}{\left( r ^{2}-\ell^{2}\right)^{2}}$
Magnetic field due to a bar magnet at an axial point has same direction as that of its magnetic dipole moment vector.
For a bar magnet of very small length $\ell<< r \overrightarrow{ B }_{ axial }=\frac{\mu_{0}}{4 \pi} \frac{2 \overrightarrow{ M }}{r^{3}}$
Browse More Topics Related Magnetism:
On Equatorial Point or Broadside Position
The magnetic field $\overrightarrow{ B }_{\text {equi }}$ at a point P due to bar magnet will be the resultant of the magnetic fields $\overrightarrow{ B _{1}}$ due to N-pole of magnet and $\overrightarrow{ B _{2}}$ due to S-pole of magnet $\overrightarrow{ B }_{ equi }=\overrightarrow{ B _{1}}+\overrightarrow{ B _{2}}$ due to S-pole of magnet $\overrightarrow{ B }_{ equ i }=\overrightarrow{ B _{1}}+\overrightarrow{ B _{2}}$$\left|\overrightarrow{ B }_{1}\right|=\frac{\mu_{0}}{4 \pi} \frac{ m }{ NP ^{2}}=\frac{\mu_{0}}{4 \pi} \frac{ m }{ r ^{2}+\ell^{2}}$ along $NP$
$\left|\overrightarrow{ B }_{2}\right|=\frac{\mu_{0}}{4 \pi} \frac{ m }{ SP ^{2}}=\frac{\mu_{0}}{4 \pi} \frac{ m }{\left( r ^{2}+\ell^{2}\right)}$ along $PS$

So $\left|\vec{B}_{1}\right|=\left|\vec{B}_{2}\right|$ On resolving $\vec{B}_{1}$ and $\overrightarrow{ B _{2}}$ along PX' and PY we find $\left|\vec{B}_{1}\right|$ $\sin \theta$ and $|\overrightarrow {{B_2}} |\,\sin \theta $
are equal and opposite so they cancel each other. So resultant field
$\overrightarrow{\mathrm{B}}_{\text {equi }}=\overrightarrow{\mathrm{B}}_{1} \cos \theta(-\hat{\mathrm{r}})+\overrightarrow{\mathrm{B}}_{2} \cos \theta(-\hat{\mathrm{r}})$
$=\left[\frac{\mu_{0}}{4 \pi} \frac{m}{\left(r^{2}+\ell^{2}\right)} \cos \theta+\frac{\mu_{0}}{4 \pi} \frac{m}{\left(r^{2}+\ell^{2}\right)} \cos \theta\right](-\hat{r})$
$=2 \cdot \frac{\mu_{0}}{4 \pi} \frac{ m }{\left( r ^{2}+\ell^{2}\right)} \cdot \frac{\ell}{\sqrt{ r ^{2}+\ell^{2}}}(-\hat{ r })$
$\overrightarrow{ B }_{ equi }=-\frac{\mu_{0}}{4 \pi} \frac{\overrightarrow{ M }}{\left( r ^{2}+\ell^{2}\right)^{\frac{3}{2}}}$
$\overrightarrow{ B }_{ equi }=-\frac{\mu_{0}}{4 \pi} \frac{\overrightarrow{ M }}{\left( r ^{2}+\ell^{2}\right)^{\frac{3}{2}}}$
The direction of magnetic field at a point on equitorial line is opposite to magnetic dipole moment vector.
For a bar magnet of very small length $\overrightarrow{ B }_{ equi }=-\frac{\mu_{0}}{4 \pi} \frac{\overrightarrow{ M }}{r^{3}}$
At An Arbitrary Point
The point P is on axial line of magnet S'N' with magnetic moment Mcos$\theta $ Magnetic flux density $B _{1}=\frac{\mu_{0}}{4 \pi} \frac{2 M \cos \theta}{ r ^{3}}$The point P is simultaneously on the equatorial line of other magnet N"S" with magnetic moment Msin $\theta $ Magnetic flux density $B _{2}=\frac{\mu_{0}}{4 \pi} \frac{ M \sin \theta}{ r ^{3}}$
Total magnetic flux density at P.
$B =\sqrt{ B _{1}^{2}+ B _{2}^{2}}=\frac{\mu_{0}}{4 \pi} \frac{ M }{ r ^{3}} \sqrt{4 \cos ^{2} \theta+\sin ^{2} \theta}$ or
$\tan \theta^{\prime}=\frac{B_{2}}{B_{1}}=\frac{\frac{\mu_{0}}{4 \pi} \frac{M \sin \theta}{r^{3}}}{\frac{\mu_{0}}{4 \pi} \frac{2 M \cos \theta}{r^{3}}}=\frac{1}{2} \tan \theta$ or $\theta^{\prime}=\tan ^{-1}\left(\frac{1}{2} \tan \theta\right)$

Also Read:
Click here for the Video tutorials of Magnetic Effect of Current Class 12
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.For free video lectures and complete study material, Download eSaral APP.
