An object moving in a plane is said to have two-dimensional motion. If you want to learn more about Motion in two dimensions. Then read this article till the end.
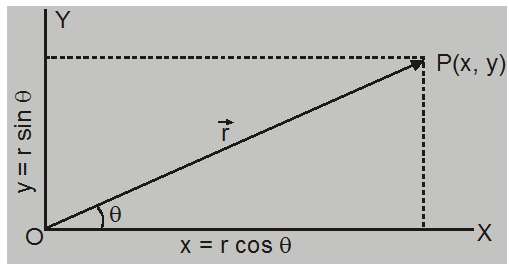
Let the position of point P at a time t be given by position
vector $\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{r}}$
$\vec{r}=\hat{i} r \cos \theta+\hat{j} r \sin \theta$
$=\hat{i} x+\hat{j} y$
position Q is given by position vector $\vec{r}_{2}=x_{2} \hat{i}+y_{2} \hat{j}$
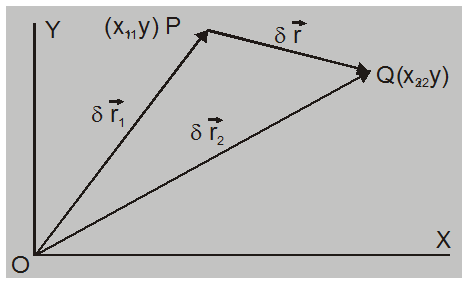
from $\Delta \mathrm{OPQ} \Rightarrow \overrightarrow{\mathrm{OP}}+\overrightarrow{\mathrm{PQ}}=\overrightarrow{\mathrm{OQ}}$
or $\quad \overrightarrow{\mathrm{PQ}}=\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}}$
Displacement $\overrightarrow{P Q}=\delta \vec{r}=\vec{r}_{2}-\vec{r}_{1}$
in time interval $\delta \mathrm{t}=\left(\mathrm{t}_{2}-\mathrm{t}_{1}\right)$
or
$\vec{\delta}_{r}=\left(x_{2} \hat{i}+y_{2} \hat{j}\right)-\left(x_{1} \hat{i}+y_{1} \hat{j}\right)$
$=\left(x_{2}-x_{1}\right) \hat{i}+\left(y_{2}-y_{1}\right) \hat{j}$
$=\delta \mathrm{x} \hat{\mathrm{i}}+8 \mathrm{y} \hat{\mathrm{j}}$
displacement along X-axis $\delta x=x_{2}-x_{1}$
displacement along Y-axis $\delta y=y_{2}-y_{1}$
Thus, displacement in 2 dimensions is equal to the vector sum of two one dimensional displacements along mutually perpendicular directions.
Let particle move with uniform velocity at $\overrightarrow{\mathrm{V}}$ an angle $\theta$ with X-axis.
Then in component form $\overrightarrow{\mathrm{v}}=\mathrm{v}_{\mathrm{x}} \hat{\mathrm{i}}+\mathrm{v}_{\mathrm{y}} \hat{\mathrm{j}}$
here $v_{x}=v \cos \theta$
and $\quad v_{y}=v \sin \theta$
and $\quad \delta \mathrm{x}=\mathrm{v}_{\mathrm{x}} \delta \mathrm{t}$
$\delta \mathrm{y}=\mathrm{v}_{\mathrm{y}} \delta \mathrm{t}$
or $\delta x=(v \cos \theta) \delta t$
$\delta y=(v \sin \theta) \delta t$
so with $\mathrm{V}_{\mathrm{x}}$ we get displacement along X-axis only and $\mathrm{v}_{\mathrm{y}}$ gives displacement along Y-axis only.
And if particle is moving with uniform acceleration $\overrightarrow{\mathrm{a}}$, then
$\overrightarrow{\mathrm{a}}=\mathrm{a}_{\mathrm{x}} \hat{\mathrm{i}}+\mathrm{a}_{\mathrm{y}} \hat{\mathrm{j}}$
If direction of $\vec{a}$ makes angle $\phi$ with X-axis then $a_{x}=a \cos \phi$ and $\mathrm{a}_{\mathrm{y}}=\mathrm{a} \sin \phi$
are components of $\overrightarrow{\mathrm{a}}$.
Due to $\mathrm{a}_{\mathrm{x}}$, there is a change in the X component of velocity only with no change in Y-component.
Similarly, $\mathrm{a}_{\mathrm{y}}$ will change only the Y component of velocity at time t
So $v_{x}=u_{x}+a_{x} t$
(here $\mathrm{u}_{\mathrm{x}}$ and $\mathrm{u}_{\mathrm{y}}$ are components of initial velocity)
And
$v_{y}=u_{y}+a_{y} t$
Hence
$v_{x} \hat{i}+v_{y} \hat{j}=\left(u_{x}+a_{x} t\right) \hat{i}+\left(u_{y}+a_{y} t\right) \hat{j}$
$=\left(u_{x} \hat{i}+u_{y} \hat{j}\right)+\left(a_{x} \hat{i}+a_{y} \hat{j}\right) t$
Or
$\overrightarrow{\mathrm{v}}=\overrightarrow{\mathrm{u}}+\overrightarrow{\mathrm{a}} \mathrm{t}$
and similarly, component of displacement are
$s_{x}=u_{x} t+\frac{1}{2} a_{x} t^{2}$
And
$s_{y}=u_{y} t+\frac{1}{2} a_{y} t^{2}$
Hence
$s_{x} \hat{i}+s_{y} \hat{j}=\left(u_{x} \hat{i}+u_{y} \hat{j}\right)+\frac{1}{2}\left(a_{x} \hat{i}+a_{y} \hat{j}\right) t^{2}$
Or
$\vec{s}=\vec{u} t+\frac{1}{2} \vec{a} t^{2}$
So, that's all from this blog. I hope you get the idea about motion in two dimensions. If you liked this explanation then don't forget to share this article with your friends.
Also read
Newtons Laws of Motion
To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
Motion in Two Dimensions
An object moving in a plane is said to have two-dimensional motion. The two-dimensional motion is equal to the vector sum of two one-dimensional motions along a mutually perpendicular direction.
Let the position of point P at a time t be given by position
vector $\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{r}}$
$\vec{r}=\hat{i} r \cos \theta+\hat{j} r \sin \theta$
$=\hat{i} x+\hat{j} y$
Displacement
Let the position of point P at time $\mathrm{t}_{1}$ be described by position vector $\vec{r}_{1}=x_{1} \hat{i}+y_{1} \hat{j}$ and at time $\mathrm{t}_{2}$position Q is given by position vector $\vec{r}_{2}=x_{2} \hat{i}+y_{2} \hat{j}$

from $\Delta \mathrm{OPQ} \Rightarrow \overrightarrow{\mathrm{OP}}+\overrightarrow{\mathrm{PQ}}=\overrightarrow{\mathrm{OQ}}$
or $\quad \overrightarrow{\mathrm{PQ}}=\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}}$
Displacement $\overrightarrow{P Q}=\delta \vec{r}=\vec{r}_{2}-\vec{r}_{1}$
in time interval $\delta \mathrm{t}=\left(\mathrm{t}_{2}-\mathrm{t}_{1}\right)$
or
$\vec{\delta}_{r}=\left(x_{2} \hat{i}+y_{2} \hat{j}\right)-\left(x_{1} \hat{i}+y_{1} \hat{j}\right)$
$=\left(x_{2}-x_{1}\right) \hat{i}+\left(y_{2}-y_{1}\right) \hat{j}$
$=\delta \mathrm{x} \hat{\mathrm{i}}+8 \mathrm{y} \hat{\mathrm{j}}$
displacement along X-axis $\delta x=x_{2}-x_{1}$
displacement along Y-axis $\delta y=y_{2}-y_{1}$
Thus, displacement in 2 dimensions is equal to the vector sum of two one dimensional displacements along mutually perpendicular directions.
Let particle move with uniform velocity at $\overrightarrow{\mathrm{V}}$ an angle $\theta$ with X-axis.
Then in component form $\overrightarrow{\mathrm{v}}=\mathrm{v}_{\mathrm{x}} \hat{\mathrm{i}}+\mathrm{v}_{\mathrm{y}} \hat{\mathrm{j}}$
here $v_{x}=v \cos \theta$
and $\quad v_{y}=v \sin \theta$
and $\quad \delta \mathrm{x}=\mathrm{v}_{\mathrm{x}} \delta \mathrm{t}$
$\delta \mathrm{y}=\mathrm{v}_{\mathrm{y}} \delta \mathrm{t}$
or $\delta x=(v \cos \theta) \delta t$
$\delta y=(v \sin \theta) \delta t$
so with $\mathrm{V}_{\mathrm{x}}$ we get displacement along X-axis only and $\mathrm{v}_{\mathrm{y}}$ gives displacement along Y-axis only.
And if particle is moving with uniform acceleration $\overrightarrow{\mathrm{a}}$, then
$\overrightarrow{\mathrm{a}}=\mathrm{a}_{\mathrm{x}} \hat{\mathrm{i}}+\mathrm{a}_{\mathrm{y}} \hat{\mathrm{j}}$
If direction of $\vec{a}$ makes angle $\phi$ with X-axis then $a_{x}=a \cos \phi$ and $\mathrm{a}_{\mathrm{y}}=\mathrm{a} \sin \phi$
are components of $\overrightarrow{\mathrm{a}}$.
Due to $\mathrm{a}_{\mathrm{x}}$, there is a change in the X component of velocity only with no change in Y-component.
Similarly, $\mathrm{a}_{\mathrm{y}}$ will change only the Y component of velocity at time t
So $v_{x}=u_{x}+a_{x} t$
(here $\mathrm{u}_{\mathrm{x}}$ and $\mathrm{u}_{\mathrm{y}}$ are components of initial velocity)
And
$v_{y}=u_{y}+a_{y} t$
Hence
$v_{x} \hat{i}+v_{y} \hat{j}=\left(u_{x}+a_{x} t\right) \hat{i}+\left(u_{y}+a_{y} t\right) \hat{j}$
$=\left(u_{x} \hat{i}+u_{y} \hat{j}\right)+\left(a_{x} \hat{i}+a_{y} \hat{j}\right) t$
Or
$\overrightarrow{\mathrm{v}}=\overrightarrow{\mathrm{u}}+\overrightarrow{\mathrm{a}} \mathrm{t}$
and similarly, component of displacement are
$s_{x}=u_{x} t+\frac{1}{2} a_{x} t^{2}$
And
$s_{y}=u_{y} t+\frac{1}{2} a_{y} t^{2}$
Hence
$s_{x} \hat{i}+s_{y} \hat{j}=\left(u_{x} \hat{i}+u_{y} \hat{j}\right)+\frac{1}{2}\left(a_{x} \hat{i}+a_{y} \hat{j}\right) t^{2}$
Or
$\vec{s}=\vec{u} t+\frac{1}{2} \vec{a} t^{2}$
So, that's all from this blog. I hope you get the idea about motion in two dimensions. If you liked this explanation then don't forget to share this article with your friends.
Also read
Newtons Laws of Motion
To watch Free Learning Videos on physics by Saransh Gupta sir Install the eSaral App.
