Motion of Charged Particle in Electric and Magnetic Field | Moving Charges and Magnetism Class 12, JEE & NEET

The motion of a charged particles in an electric and magnetic field (in the simultaneous presence of both ) has a variety of manifestations ranging from straight-line motion to the cycloid and other complex motion. Both electric and magnetic fields impart acceleration to the charged particle. But, there is a qualification for the magnetic field as acceleration due to magnetic field relates only to the change of direction of motion. The magnetic force being always normal to the velocity of the particle tends to move the particle about a circular trajectory. On the other hand, the electric force is along the electric field and is capable to bring about change in both direction and magnitude depending upon the initial direction of the velocity of the charged particle with respect to the electric field. If velocity and electric vectors are at an angle then the particle follows a parabolic path.

1. Motion of a charged Particle in Combined Electric and Magnetic fields
2. Difference of Motion of a Charged Particle in Magnetic Field and Electric Field

One of the important orientations of electric and magnetic fields is referred to as “crossed fields”. We use the term “crossed fields” to mean the simultaneous presence of electric and magnetic fields at a right angle. The behavior of charged particles such as electrons under crossed fields has important significance in the study of electromagnetic measurement and application (determination of specific charge of the electron, cyclotron, etc.).

Motion of charged Particle in Combined Electric and Magnetic fields

Let a moving charged particle is subjected simultaneously to both electric field $\overrightarrow{\mathrm{E}}$ and magneticfield $\overrightarrow{\mathrm{B}}$

The moving charged particle will experience electric force $\overrightarrow{\mathrm{F}_{\mathrm{e}}}=\mathrm{qE}$

And magnetic force $\overrightarrow{\mathrm{F}_{\mathrm{m}}}=\mathrm{q}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})$



Depending on the direction of $\overrightarrow{\mathrm{v}}, \overrightarrow{\mathrm{E}}$ and $\overrightarrow{\mathrm{B}}$ various situation are possible and the motion in general is quite complex.

CASE 1

case I $: \overrightarrow{\mathbf{v}}, \overrightarrow{\mathbf{E}}$ and $\overrightarrow{\mathbf{B}}$ all the three are collinear :

As the particle is moving parallel or antiparallel to the field. The magnetic force on it will be zero

And only electric force will act

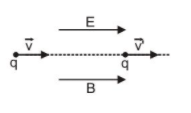So, acceleration of the particle $\vec{a}=\frac{\vec{F}}{m}=\frac{q \vec{E}}{m}$

Hence, the particle will pass through the field following a straight line path (parallel to the field) with change in its speed.

In this situation speed, velocity, momentum and kinetic energy all will change without change in direction of motion as shown in figure above.

CASE 2

case II : $: \vec{v}, \vec{E}$ and $\vec{B}$ are mutually perpendicular :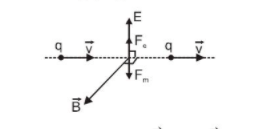

If in this situation direction and magnitude of $\overrightarrow{\mathrm{E}}$ and $\overrightarrow{\mathrm{B}}$ are such that



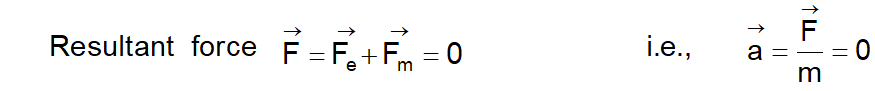
Then as shown in fig., the particle will pass through the field with same velocity



OR $v=\frac{E}{B}$

This principle is used in 'Velocity-selector' to get a charged beam having a specific velocity.

Difference of Motion of a Charged Particle in Magnetic Field and Electric Field

Also Read: Biot Savart's Law

Click here for the Video tutorials of Magnetic Effect of Current Class 12

About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.

For free video lectures and complete study material, Download eSaral APP.