NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism PDF

Hey, are you a class 12 student and looking for ways to download NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism PDF? If yes. Then read this post till the end.

In this article, we have listed NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism in PDF that are prepared by Kota’s top IITian Faculties by keeping Simplicity in mind.

If you want to learn and understand class 12 Physics Chapter 4 "Moving Charges and Magnetism PDF" in an easy way then you can use these solutions PDF.

NCERT Solutions helps students to Practice important concepts of subjects easily. Class 12 Physics solutions provide detailed explanations of all the NCERT questions that students can use to clear their doubts instantly.

If you want to score high in your class 12 Physics Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.

In this article, we have listed NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism PDF that you can download to start your preparations anytime.

So, without wasting more time Let’s start.

Download NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism PDF

Question $1$ : A circular coil of wire consisting of 100 turns, each of radius $8.0 \mathrm{~cm}$ carries a current of $0.40 \mathrm{~A}$. What is the magnitude of the magnetic field $\mathbf{B}$ at the centre of the coil?

Solution. Number of turns on the circular coil, $n=100$

Radius of each turn, $r=8.0 \mathrm{~cm}=0.08 \mathrm{~m}$

Current flowing in the coil, $I=0.4 \mathrm{~A}$

Magnitude of the magnetic field at the centre of the coil is given by the relation,

$|\mathbf{B}|=\frac{\mu_{0}}{4 \pi} \frac{2 \pi n I}{r}$

Where,

$\mu_{0}=$ Permeability of free space

$=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

$|\mathbf{B}|=\frac{4 \pi \times 10^{-7}}{4 \pi} \times \frac{2 \pi \times 100 \times 0.4}{0.08}$

$=3.14 \times 10^{-4} \mathrm{~T}$

Hence, the magnitude of the magnetic field is $3.14 \times 10^{-4} \mathrm{~T}$.

Question 2: A long straight wire carries a current of $35 \mathrm{~A}$. What is the magnitude of the field $\mathbf{B}$ at a point $20 \mathrm{~cm}$ from the wire?

Solution. Current in the wire, $l=35 \mathrm{~A}$

Distance of a point from the wire, $r=20 \mathrm{~cm}=0.2 \mathrm{~m}$

Magnitude of the magnetic field at this point is given as:

$B=\frac{\mu_{0}}{4 \pi} \frac{2 I}{r}$

Where,

$\mu_{0}=$ Permeability of free space $=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

$B=\frac{4 \pi \times 10^{-7} \times 2 \times 35}{4 \pi \times 0.2}$

$=3.5 \times 10^{-5} \mathrm{~T}$

Hence, the magnitude of the magnetic field at a point $20 \mathrm{~cm}$ from the wire is $3.5 \times 10^{-5} \mathrm{~T}$.

Question 3: A long straight wire in the horizontal plane carries a current of $50 \mathrm{~A}$ in north to south direction. Give the magnitude and direction of $\mathbf{B}$ at a point $2.5 \mathrm{~m}$ east of the wire.

Solution. Current in the wire, $l=50 \mathrm{~A}$

A point is $2.5 \mathrm{~m}$ away from the East of the wire.

$\therefore$ Magnitude of the distance of the point from the wire, $r=2.5 \mathrm{~m}$.

Magnitude of the magnetic field at that point is given by the relation, $B=\frac{\mu_{0} 2 I}{4 \pi r}$

Where,

$\mu_{0}=$ Permeability of free space $=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

$B=\frac{4 \pi \times 10^{-7} \times 2 \times 50}{4 \pi \times 2.5}$

$=4 \times 10^{-6} \mathrm{~T}$

The point is located normal to the wire length at a distance of $2.5 \mathrm{~m}$. The direction of the current in the wire is vertically downward. Hence, according to the Maxwell's right hand thumb rule, the direction of the magnetic field at the given point is vertically upward.

Question 4: A horizontal overhead power line carries a current of $90 \mathrm{~A}$ in east to west direction. What is the magnitude and direction of the magnetic field due to the current $1.5 \mathrm{~m}$ below the line?

Solution. Current in the power line, $I=90 \mathrm{~A}$

Point is located below the power line at distance, $r=1.5 \mathrm{~m}$

Hence, magnetic field at that point is given by the relation,

$B=\frac{\mu_{0} 2 I}{4 \pi r}$

Where,

$\mu_{0}=$ Permeability of free space $=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

$B=\frac{4 \pi \times 10^{-7} \times 2 \times 90}{4 \pi \times 1.5}=1.2 \times 10^{-5} \mathrm{~T}$

The current is flowing from East to West. The point is below the power line. Hence, according to Maxwell’s right hand thumb rule, the direction of the magnetic field is towards the South.

Question 5: What is the magnitude of magnetic force per unit length on a wire carrying a current of $8 \mathrm{~A}$ and making an angle of $30^{\circ}$ with the direction of a uniform magnetic field of $0.15 \mathrm{~T} ?$

Solution. Current in the wire, $I=8 \mathrm{~A}$

Magnitude of the uniform magnetic field, $B=0.15 \mathrm{~T}$

Angle between the wire and magnetic field, $\theta=30^{\circ}$.

Magnetic force per unit length on the wire is given as:

$f=B / \sin \theta$

$=0.15 \times 8 \times 1 \times \sin 30^{\circ}$

$=0.6 \mathrm{~N} \mathrm{~m}^{-1}$

Hence, the magnetic force per unit length on the wire is $0.6 \mathrm{~N} \mathrm{~m}^{-1}$.

Question 6: A $3.0 \mathrm{~cm}$ wire carrying a current of $10 \mathrm{~A}$ is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be $0.27 \mathrm{~T}$. What is the magnetic force on the wire?

Solution. Length of the wire, $l=3 \mathrm{~cm}=0.03 \mathrm{~m}$

Current flowing in the wire, $l=10 \mathrm{~A}$

Magnetic field, $B=0.27 \mathrm{~T}$

Angle between the current and magnetic field, $\theta=90^{\circ}$

Magnetic force exerted on the wire is given as:

$F=B / / \sin \theta$

$=0.27 \times 10 \times 0.03 \sin 90^{\circ}$

$=8.1 \times 10^{-2} \mathrm{~N}$

Hence, the magnetic force on the wire is $8.1 \times 10^{-2} \mathrm{~N}$. The direction of the force can be obtained from Fleming's left hand rule

Question 7: Two long and parallel straight wires $\mathrm{A}$ and $\mathrm{B}$ carrying currents of $8.0 \mathrm{~A}$ and $5.0 \mathrm{~A}$ in the same direction are separated by a distance of $4.0 \mathrm{~cm}$. Estimate the force on a $10 \mathrm{~cm}$ section of wire $\mathrm{A}$.

Solution. Current flowing in wire $A, I_{A}=8.0 \mathrm{~A}$

Current flowing in wire $\mathrm{B}, I_{\mathrm{B}}=5.0 \mathrm{~A}$

Distance between the two wires, $r=4.0 \mathrm{~cm}=0.04 \mathrm{~m}$

Length of a section of wire $\mathrm{A}_{1} /=10 \mathrm{~cm}=0.1 \mathrm{~m}$

Force exerted on length $/$ due to the magnetic field is given as:

$B=\frac{\mu_{0} 2 I_{\mathrm{A}} I_{\mathrm{B}} l}{4 \pi r}$

Where,

$\mu_{0}=$ Permeability of free space $=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

$B=\frac{4 \pi \times 10^{-7} \times 2 \times 8 \times 5 \times 0.1}{4 \pi \times 0.04}$

$=2 \times 10^{-5} \mathrm{~N}$

The magnitude of force is $2 \times 10^{-5} \mathrm{~N}$. This is an attractive force normal to A towards $\mathrm{B}$ because the direction of the currents in the wires is the same.

Question 8: A closely wound solenoid $80 \mathrm{~cm}$ long has 5 layers of windings of 400 turns each. The diameter of the solenoid is $1.8 \mathrm{~cm}$. If the current carried is $8.0 \mathrm{~A}$, estimate the magnitude of $\mathrm{B}$ inside the solenoid near its centre.

Solution. Length of the solenoid, $I=80 \mathrm{~cm}=0.8 \mathrm{~m}$

There are five layers of windings of 400 turns each on the solenoid.

$\therefore$ Total number of turns on the solenoid, $N=5 \times 400=2000$

Diameter of the solenoid, $D=1.8 \mathrm{~cm}=0.018 \mathrm{~m}$

Current carried by the solenoid, $I=8.0 \mathrm{~A}$

Magnitude of the magnetic field inside the solenoid near its centre is given by the relation,

$B=\frac{\mu_{0} N I}{l}$

Where,

$\mu_{0}=$ Permeability of free space $=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

$B=\frac{4 \pi \times 10^{-7} \times 2000 \times 8}{0.8}$

$=8 \pi \times 10^{-3}=2.512 \times 10^{-2} \mathrm{~T}$

Hence, the magnitude of the magnetic field inside the solenoid near its centre is $2.512 \times 10^{-2} \mathrm{~T}$.

Question $9$ A square coil of side $10 \mathrm{~cm}$ consists of 20 turns and carries a current of $12 \mathrm{~A}$. The coil is suspended vertically and the normal to the plane of the coil makes an angle of $30^{\circ}$ with the direction of a uniform horizontal magnetic field of magnitude $0.80 \mathrm{~T}$. What is the magnitude of torque experienced by the coil?

Solution. Length of a side of the square coil, $1=10 \mathrm{~cm}=0.1 \mathrm{~m}$

Current flowing in the coil, $I=12 \mathrm{~A}$

Number of turns on the coil, $n=20$

Angle made by the plane of the coil with magnetic field, $\theta=30^{\circ}$

Strength of magnetic field, $B=0.80 \mathrm{~T}$

Magnitude of the magnetic torque experienced by the coil in the magnetic field is given by the relation,

$\mathrm{T}=n B I A \sin \theta$

Where,

$A=$ Area of the square coil

$\Rightarrow / \times 1=0.1 \times 0.1=0.01 \mathrm{~m}^{2}$

$\therefore \mathrm{T}=20 \times 0.8 \times 12 \times 0.01 \times \sin 30^{\circ}$

$=0.96 \mathrm{~N} \mathrm{~m}$

Hence, the magnitude of the torque experienced by the coil is $0.96 \mathrm{~N} \mathrm{~m}$.

Question 10: Two moving coil meters, $M_{1}$ and $M_{2}$ have the following particulars:

$R_{1}=10 \Omega, N_{1}=30$

$A_{1}=3.6 \times 10^{-3} \mathrm{~m}^{2}, B_{1}=0.25 \mathrm{~T}$

$R_{2}=14 \Omega, N_{2}=42$

$A_{2}=1.8 \times 10^{-3} \mathrm{~m}^{2}, B_{2}=0.50 \mathrm{~T}$

(The spring constants are identical for the two meters).

Determine the ratio of (a) current sensitivity and (b) voltage sensitivity of $\mathrm{M}_{2}$ and $\mathrm{M}_{1}$.

Solution. For moving coil meter $\mathrm{M}_{1}$ :

Resistance, $R_{1}=10 \Omega$

Number of turns, $N_{1}=30$

Area of cross-section, $A_{1}=3.6 \times 10^{-3} \mathrm{~m}^{2}$

Magnetic field strength, $B_{1}=0.25 \mathrm{~T}$

Spring constant $K_{1}=K$

For moving coil meter $\mathrm{M}_{2}$ :

Resistance, $R_{2}=14 \Omega$

Number of turns, $N_{2}=42$

Area of cross-section, $A_{2}=1.8 \times 10^{-3} \mathrm{~m}^{2}$

Magnetic field strength, $B_{2}=0.50 \mathrm{~T}$

Spring constant, $K_{2}=K$

(a) Current sensitivity of $M_{1}$ is given as:

$I_{\mathrm{sl}}=\frac{N_{1} B_{1} A_{1}}{K_{1}}$

And, current sensitivity of $M_{2}$ is given as:

$I_{\mathrm{s} 2}=\frac{N_{2} B_{2} A_{2}}{K_{2}}$

$\therefore$ Ratio $\frac{I_{s 2}}{I_{\mathrm{sl}}}=\frac{N_{2} B_{2} A_{2} K_{1}}{K_{2} N_{1} B_{1} A_{1}}$

$=\frac{42 \times 0.5 \times 1.8 \times 10^{-3} \times K}{K \times 30 \times 0.25 \times 3.6 \times 10^{-3}}=1.4$

Hence, the ratio of current sensitivity of $\mathrm{M}_{2}$ to $\mathrm{M}_{1}$ is $1.4$.

(b) Voltage sensitivity for $\mathrm{M}_{2}$ is given as:

$V_{\mathrm{s} 2}=\frac{N_{2} B_{2} A_{2}}{K_{2} R_{2}}$

And, voltage sensitivity for $\mathrm{M}_{1}$ is given as:

$V_{s 1}=\frac{N_{1} B_{1} A_{1}}{K_{1} R_{1}}$

$\therefore$ Ratio $\frac{V_{s 2}}{V_{s 1}}=\frac{N_{2} B_{2} A_{2} K_{1} R_{1}}{K_{2} R_{2} N_{1} B_{1} A_{1}}$

$=\frac{42 \times 0.5 \times 1.8 \times 10^{-3} \times 10 \times K}{K \times 14 \times 30 \times 0.25 \times 3.6 \times 10^{-3}}=1$

Hence, the ratio of voltage sensitivity of $\mathrm{M}_{2}$ to $\mathrm{M}_{1}$ is 1 .

Question 11: path of the electron is a circle. Determine the radius of the circular orbit. $\left(\mathrm{e}=1.6 \times 10^{-19} \mathrm{C}, \mathrm{m}_{\mathrm{e}}=9.1 \times 10^{-31} \mathrm{~kg}\right)$

Solution. Magnetic field strength, $B=6.5 \mathrm{G}=6.5 \times 10^{-4} \mathrm{~T}$

Speed of the electron, $v=4.8 \times 10^{6} \mathrm{~m} / \mathrm{s}$

Charge on the electron, $e=1.6 \times 10^{-19} \mathrm{C}$

Mass of the electron, $m_{e}=9.1 \times 10^{-31} \mathrm{~kg}$

Angle between the shot electron and magnetic field, $\theta=90^{\circ}$

Magnetic force exerted on the electron in the magnetic field is given as:

$F=e v B \sin \theta$

This force provides centripetal force to the moving electron. Hence, the electron starts moving in a circular path of radius $r$.

Hence, centripetal force exerted on the electron,

$F_{\mathrm{c}}=\frac{m v^{2}}{r}$

In equilibrium, the centripetal force exerted on the electron is equal to the magnetic force i.e.

$F_{\mathrm{c}}=F$

$\frac{m v^{2}}{r}=e v B \sin \theta$

$r=\frac{m v}{B e \sin \theta}$

$=\frac{9.1 \times 10^{-31} \times 4.8 \times 10^{6}}{6.5 \times 10^{-4} \times 1.6 \times 10^{-19} \times \sin 90^{\circ}}$

$=4.2 \times 10^{-2} \mathrm{~m}=4.2 \mathrm{~cm}$

Hence, the radius of the circular orbit of the electron is $4.2 \mathrm{~cm}$.

Question 12: In Exercise $4.11$ obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain.

Solution. Magnetic field strength, $B=6.5 \times 10^{-4} \mathrm{~T}$

Charge of the electron, $e=1.6 \times 10^{-19} \mathrm{C}$

Mass of the electron, $m_{e}=9.1 \times 10^{-31} \mathrm{~kg}$

Velocity of the electron, $v=4.8 \times 10^{6} \mathrm{~m} / \mathrm{s}$

Radius of the orbit, $r=4.2 \mathrm{~cm}=0.042 \mathrm{~m}$

Frequency of revolution of the electron $=\mathrm{V}$

Angular frequency of the electron $=\omega=2 \pi v$

Velocity of the electron is related to the angular frequency as:

$v=r \omega$

In the circular orbit, the magnetic force on the electron is balanced by the centripetal force. Hence, we can write:

$e v B=\frac{m v^{2}}{r}$

$e B=\frac{m}{r}(r \omega)=\frac{m}{r}(r 2 \pi v)$

$v=\frac{B e}{2 \pi m}$

This expression for frequency is independent of the speed of the electron.

On substituting the known values in this expression, we get the frequency as:

$v=\frac{6.5 \times 10^{-4} \times 1.6 \times 10^{-19}}{2 \times 3.14 \times 9.1 \times 10^{-31}}$

$=18.2 \times 10^{6} \mathrm{~Hz}$

$\approx 18 \mathrm{MHz}$

Hence, the frequency of the electron is around $18 \mathrm{MHz}$ and is independent of the speed of the electron.

Question $13$ : (a) A circular coil of 30 turns and radius $8.0 \mathrm{~cm}$ carrying a current of $6.0 \mathrm{~A}$ is suspended vertically in a uniform horizontal magnetic field of magnitude $1.0 \mathrm{~T}$. The field lines make an angle of $60^{\circ}$ with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil from turning

(b) Would your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area? (All other particulars are also unaltered.)

Solution. (a) Number of turns on the circular coil, $n=30$

Radius of the coil, $r=8.0 \mathrm{~cm}=0.08 \mathrm{~m}$

Area of the coil $=\pi r^{2}=\pi(0.08)^{2}=0.0201 \mathrm{~m}^{2}$

Current flowing in the coil, $I=6.0 \mathrm{~A}$

Magnetic field strength, $B=1 \mathrm{~T}$

Angle between the field lines and normal with the coil surface,

$\theta=60^{\circ}$

The coil experiences a torque in the magnetic field. Hence, it turns. The counter torque applied to prevent the coil from turning is given by the relation,

$\mathrm{T}=n / B A \sin \theta \ldots(i)$

$=30 \times 6 \times 1 \times 0.0201 \times \sin 60^{\circ}$

$=3.133 \mathrm{~N} \mathrm{~m}$

(b) It can be inferred from relation (i) that the magnitude of the applied torque is not dependent on the shape of the coil. It depends on the area of the coil. Hence, the answer would not change if the circular coil in the above case is replaced by a planar coil of some irregular shape that encloses the same area

Question 14: Two concentric circular coils $\mathrm{X}$ and $\mathrm{Y}$ of radii $16 \mathrm{~cm}$ and $10 \mathrm{~cm}$, respectively, lie in the same vertical plane containing the north to south direction. Coil $\mathrm{X}$ has 20 turns and carries: current of $16 \mathrm{~A}$; coil $\mathrm{Y}$ has 25 turns and carries a current of $18 \mathrm{~A}$. The sense of the current in $\mathrm{X}$ is anticlockwise, and clockwise in $\mathrm{Y}$, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.

Solution. Radius of coil $\mathrm{X}, r_{1}=16 \mathrm{~cm}=0.16 \mathrm{~m}$

Radius of coil $\mathrm{Y}, r_{2}=10 \mathrm{~cm}=0.1 \mathrm{~m}$

Number of turns of on coil $\mathrm{X}, n_{1}=20$

Number of turns of on coil $Y, n_{2}=25$

Number of turns of on coil $\mathrm{Y}, n_{2}=25$

Current in coil $\mathrm{X}, I_{1}=16 \mathrm{~A}$

Current in coil $\mathrm{Y}, I_{2}=18 \mathrm{~A}$

Magnetic field due to coil $X$ at their centre is given by the relation,

$B_{1}=\frac{\mu_{0} n_{1} I_{\mathrm{I}}}{2 r_{1}}$

Where,

$\mu_{0}=$ Permeability of free space $=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

$\therefore B_{1}=\frac{4 \pi \times 10^{-7} \times 20 \times 16}{2 \times 0.16}$

$=4 \pi \times 10^{-4} \mathrm{~T}$ (towards East)

Magnetic field due to coil Y at their centre is given by the relation,

$B_{2}=\frac{\mu_{0} n_{2} I_{2}}{2 r_{2}}$

$=\frac{4 \pi \times 10^{-7} \times 25 \times 18}{2 \times 0.10}$

$=9 \pi \times 10^{-4} \mathrm{~T}$ (towards West)

Hence, net magnetic field can be obtained as:

$B=B_{2}-B_{1}$

$=9 \pi \times 10^{-4}-4 \pi \times 10^{-4}$

$=5 \pi \times 10^{-4} \mathrm{~T}$

$=1.57 \times 10^{-3} \mathrm{~T}$ (towards West)

Question 15: A magnetic field of $100 \mathrm{G}\left(1 \mathrm{G}=10^{-4} \mathrm{~T}\right)$ is required which is uniform in a region of linear dimension about $10 \mathrm{~cm}$ and area of cross-section about $10^{-3} \mathrm{~m}^{2}$. The maximum current- particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic

Solution. Magnetic field strength, $B=100 \mathrm{G}=100 \times 10^{-4} \mathrm{~T}$

Number of turns per unit length, $n=1000$ turns $\mathrm{m}^{-1}$

Current flowing in the coil, $I=15 \mathrm{~A}$

Permeability of free space, $\mu_{0}=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

Magnetic field is given by the relation,

$B=\mu_{0} n I$

$\therefore n I=\frac{B}{\mu_{0}}$

$=\frac{100 \times 10^{-4}}{4 \pi \times 10^{-7}}=7957.74$

$\approx 8000 \mathrm{~A} / \mathrm{m}$

If the length of the coil is taken as $50 \mathrm{~cm}$, radius $4 \mathrm{~cm}$, number of turns 400 , and current $10 \mathrm{~A}$, then these values are not unique for the given purpose. There is always a possibility of some adjustments with limits.

Question $16:$ For a circular coil of radius $R$ and $N$ turns carrying current $I$, the magnitude of the magnetic field at a point on its axis at a distance $x$ from its centre is given by,

$B=\frac{\mu_{0} I R^{2} N}{2\left(x^{2}+R^{2}\right)^{\frac{3}{2}}}$

(a) Show that this reduces to the familiar result for field at the centre of the coil.

(b) Consider two parallel co-axial circular coils of equal radius $R$, and number of turns $N$, carrying equal currents in the same direction, and separated by a distance $R$. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to $R$, and is given by,

$B=0.72-\frac{\mu_{0} B N I}{R}$, approximately.

[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]

Solution. Radius of circular coil $=R$

Number of turns on the coil $=N$

Current in the coil $=1$

Magnetic field at a point on its axis at distance $x$ is given by the relation,

$B=\frac{\mu_{0} I R^{2} N}{2\left(x^{2}+R^{2}\right)^{\frac{3}{2}}}$

Where,

$\mu_{0}=$ Permeability of free space

(a) If the magnetic field at the centre of the coil is considered, then $x=0$.

$\therefore B=\frac{\mu_{0} I R^{2} N}{2 R^{3}}=\frac{\mu_{0} I N}{2 R}$

This is the familiar result for magnetic field at the centre of the coil.

(b) Radii of two parallel co-axial circular coils $=R$

Number of turns on each coil $=N$

Current in both coils $=1$

Distance between both the coils $=R$

Let us consider point $\mathrm{Q}$ at distance $d$ from the centre.



Then, one coil is at a distance of $\frac{R}{2}+d$ from point $Q$.

$\therefore$ Magnetic field at point $Q$ is given as:

$B_{1}=\frac{\mu_{0} N I R^{2}}{2\left[\left(\frac{R}{2}+d\right)^{2}+R^{2}\right]^{\frac{3}{2}}}$

Also, the other coil is at a distance of $\frac{R}{2}-d$ from point $Q$.

$\therefore$ Magnetic field due to this coil is given as:

$B_{2}=\frac{\mu_{0} N I R^{2}}{2\left[\left(\frac{R}{2}-d\right)^{2}+R^{2}\right]^{\frac{3}{2}}}$

Total magnetic field,

$B=B_{1}+B_{2}$

$=\frac{\mu_{0} I R^{2}}{2}\left[\left\{\left(\frac{R}{2}-d\right)^{2}+R^{2}\right\}^{-\frac{3}{2}}+\left\{\left(\frac{R}{2}+d\right)^{2}+R^{2}\right\}^{-\frac{3}{2}}\right]$

$=\frac{\mu_{0} I R^{2}}{2}\left[\left(\frac{5 R^{2}}{4}+d^{2}-R d\right)^{-\frac{3}{2}}+\left(\frac{5 R^{2}}{4}+d^{2}+R d\right)^{-\frac{3}{2}}\right]$

$=\frac{\mu_{0} I R^{2}}{2} \times\left(\frac{5 R^{2}}{4}\right)^{-\frac{3}{2}}\left[\left(1+\frac{4}{5} \frac{d^{2}}{R^{2}}-\frac{4}{5} \frac{d}{R}\right)^{-\frac{3}{2}}+\left(1+\frac{4}{5} \frac{d^{2}}{R^{2}}+\frac{4}{5} \frac{d}{R}\right)^{-\frac{3}{2}}\right]$

For $d<
$\approx \frac{\mu_{0} I R^{2}}{2} \times\left(\frac{5 R^{2}}{4}\right)^{\frac{3}{2}} \times\left[\left(1-\frac{4 d}{5 R}\right)^{-\frac{3}{2}}+\left(1+\frac{4 d}{5 R}\right)^{-\frac{3}{2}}\right]$

$\approx \frac{\mu_{0} I R^{2} N}{2 R^{3}} \times\left(\frac{4}{5}\right)^{\frac{3}{2}}\left[1-\frac{6 d}{5 R}+1+\frac{6 d}{5 R}\right]$

$B=\left(\frac{4}{5}\right)^{\frac{3}{2}} \frac{\mu_{0} I N}{R}=0.72\left(\frac{\mu_{0} I N}{R}\right)$

Hence, it is proved that the field on the axis around the mid-point between the coils is uniform.

Question 17: A toroid has a core (non-ferromagnetic) of inner radius $25 \mathrm{~cm}$ and outer radius $26 \mathrm{~cm}$, around which 3500 turns of a wire are wound. If the current in the wire is $11 \mathrm{~A}$, what is the magnetic field (a) outside the toroid, (b) inside the core of the toroid, and (c) in the empty space surrounded by the toroid.

Solution. Inner radius of the toroid, $r_{1}=25 \mathrm{~cm}=0.25 \mathrm{~m}$

Outer radius of the toroid, $r_{2}=26 \mathrm{~cm}=0.26 \mathrm{~m}$

Number of turns on the coil, $N=3500$

Current in the coil, $I=11 \mathrm{~A}$

(a) Magnetic field outside a toroid is zero. It is non-zero only inside the core of a toroid.

(b) Magnetic field inside the core of a toroid is given by the relation,

$B=\frac{\mu_{0} N I}{l}$

Where,

$\mu_{0}=$ Permeability of free space $=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

$I=$ length of toroid

$=2 \pi\left[\frac{r_{1}+r_{2}}{2}\right]$

$=\pi(0.25+0.26)$

$=0.51 \pi$

$\therefore B=\frac{4 \pi \times 10^{-7} \times 3500 \times 11}{0.51 \pi}$

$\approx 3.0 \times 10^{-2} \mathrm{~T}$

(c) Magnetic field in the empty space surrounded by the toroid is zero.

Question 18: Answer the following questions:

(a) A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?

(b) A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?

(c) An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path.

Solution. (a) The initial velocity of the particle is either parallel or anti-parallel to the magnetic field. Hence, it travels along a straight path without suffering any deflection in the field.

(b) Yes, the final speed of the charged particle will be equal to its initial speed. This is because magnetic force can change the direction of velocity, but not its magnitude.

(c) An electron travelling from West to East enters a chamber having a uniform electrostatic field in the North-South direction. This moving electron can remain undeflected if the electric force acting on it is equal and opposite of magnetic field. Magnetic force is directed towards the South. According to Fleming's left hand rule, magnetic field should be applied in a vertically downward direction.

Question $19$ : An electron emitted by a heated cathode and accelerated through a potential difference of $2.0 \mathrm{kV}$, enters a region with uniform magnetic field of $0.15 \mathrm{~T}$. Determine the trajectory of the electron if the field (a) is transverse to its initial velocity, (b) makes an angle of $30^{\circ}$ with the initial velocity.

Solution. Magnetic field strength, $B=0.15 \mathrm{~T}$

Charge on the electron, $e=1.6 \times 10^{-19} \mathrm{C}$

Mass of the electron, $m=9.1 \times 10^{-31} \mathrm{~kg}$

Potential difference, $V=2.0 \mathrm{kV}=2 \times 10^{3} \mathrm{~V}$

Thus, kinetic energy of the electron $=\mathrm{eV}$

$\Rightarrow e V=\frac{1}{2} m v^{2}$

$v=\sqrt{\frac{2 e V}{m}}$$\ldots(1)$

Where,

$v=$ velocity of the electron

(a) Magnetic force on the electron provides the required centripetal force of the electron. Hence, the electron traces a circular path of radius $r$.

Magnetic force on the electron is given by the relation,

$B \mathrm{ev}$

Centripetal force $=\frac{m v^{2}}{r}$

$\therefore B e v=\frac{m v^{2}}{r}$

$r=\frac{m v}{B e}$... (2)

From equations (1) and (2), we get

$=\frac{9.1 \times 10^{-31}}{0.15 \times 1.6 \times 10^{-19}} \times\left(\frac{2 \times 1.6 \times 10^{-19} \times 2 \times 10^{3}}{9.1 \times 10^{-31}}\right)^{\frac{1}{2}}$

$=100.55 \times 10^{-5}$

$=1 \mathrm{~mm}$

Hence, the electron has a circular trajectory of radius $1.0 \mathrm{~mm}$ normal to the magnetic field.

(b) When the field makes an angle $\theta$ of $30^{\circ}$ with initial velocity, the initial velocity will be,

$v_{1}=v \sin \theta$

From equation (2), we can write the expression for new radius as:

$r_{1,}=\frac{m v_{1}}{B e}$

$=\frac{m v \sin \theta}{B e}$

$=\frac{9.1 \times 10^{-31}}{0.15 \times 1.6 \times 10^{-19}} \times\left[\frac{2 \times 1.6 \times 10^{-

19} \times 2 \times 10^{3}}{9 \times 10^{-31}}\right]^{\frac{1}{2}} \times \sin 30^{\circ}$

$=0.5 \times 10^{-3} \mathrm{~m}$

$=0.5 \mathrm{~mm}$

Hence, the electron has a helical trajectory of radius $0.5 \mathrm{~mm}$ along the magnetic field direction.

Question $20$ : A magnetic field set up using Helmholtz coils (described in Exercise 4.16) is uniform in a small region and has a magnitude of $0.75 \mathrm{~T}$. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through $15 \mathrm{kV}$ enters this region in a as to what the beam contains. Why is the answer not unique?

Solution. Magnetic field, $B=0.75 \mathrm{~T}$

Accelerating voltage, $V=15 \mathrm{kV}=15 \times 10^{3} \mathrm{~V}$

Electrostatic field, $E=9 \times 10^{5} \mathrm{~V} \mathrm{~m}^{-1}$

Mass of the electron $=m$

Charge of the electron $=e$

Velocity of the electron $=v$

Kinetic energy of the electron $=\mathrm{eV}$

$\Rightarrow \frac{1}{2} m v^{2}=e V$

$\therefore \frac{e}{m}=\frac{v^{2}}{2 V}$$\ldots(1)$

Since the particle remains undeflected by electric and magnetic fields, we can infer that the force on the charged particle due to electric field is balancing the force on the charged particle due to magnetic field.

$\therefore e E=e v B$

$v=\frac{E}{B}$$\ldots(2)$

Putting equation (2) in equation (1), we get

$\frac{e}{m}=\frac{1}{2} \frac{\left(\frac{E}{B}\right)^{2}}{V}=\frac{E^{2}}{2 V B^{2}}$

$=\frac{\left(9.0 \times 10^{5}\right)^{2}}{2 \times 15000 \times(0.75)^{2}}=4.8 \times 10^{7} \mathrm{C} / \mathrm{kg}$

This value of specific charge elm is equal to the value of deuteron or deuterium ions. This is not a unique answer. Other possible answers are $\mathrm{He}^{++} \mathrm{Li}^{++}$, etc.

Question $21$ : A straight horizontal conducting rod of length $0.45 \mathrm{~m}$ and mass $60 \mathrm{~g}$ is suspended by two vertical wires at its ends. A current of $5.0 \mathrm{~A}$ is set up in the rod through the wires.

(a) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?

(b) What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before? (Ignore the mass of the wires.) g $=9.8 \mathrm{~m} \mathrm{~s}^{-2}$.

Solution. Length of the rod, $1=0.45 \mathrm{~m}$

Mass suspended by the wires, $m=60 \mathrm{~g}=60 \times 10^{-3} \mathrm{~kg}$

Acceleration due to gravity, $\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^{2}$

Current in the rod flowing through the wire, $I=5 \mathrm{~A}$

(a) Magnetic field ( $B$ ) is equal and opposite to the weight of the wire i.e.,

$B I l=m \mathrm{~g}$

$\therefore B=\frac{m \mathrm{~g}}{\Pi l}$ $=\frac{60 \times 10^{-3} \times 9.8}{5 \times 0.45}=0.26 \mathrm{~T}$

A horizontal magnetic field of 0.26 T normal to the length of the conductor should be set up in order to get zero tension in the wire. The magnetic field should be such that Fleming’s left hand rule gives an upward magnetic force.

(b) If the direction of the current is revered, then the force due to magnetic field and the weight of the wire acts in a vertically downward direction.

$\therefore$ Total tension in the wire $=B \|+m g$

$=0.26 \times 5 \times 0.45+\left(60 \times 10^{-3}\right) \times 9.8$

$=1.176 \mathrm{~N}$

Question 22: The wires which connect the battery of an automobile to its starting motor carry a current of $300 \mathrm{~A}$ (for a short time). What is the force per unit length between the wires if they are $70 \mathrm{~cm}$ long and $1.5 \mathrm{~cm}$ apart? Is the force attractive or repulsive?

Solution. Current in both wires, $I=300 \mathrm{~A}$

Distance between the wires, $r=1.5 \mathrm{~cm}=0.015 \mathrm{~m}$

Length of the two wires, $l=70 \mathrm{~cm}=0.7 \mathrm{~m}$

Force between the two wires is given by the relation,

$F=\frac{\mu_{0} I^{2}}{2 \pi r}$

Where,

$\mu_{0}=$ Permeability of free space $=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

$\therefore F=\frac{4 \pi \times 10^{-7} \times(300)^{2}}{2 \pi \times 0.015}$

$=1.2 \mathrm{~N} / \mathrm{m}$

Since the direction of the current in the wires is opposite, a repulsive force exists between them.

Question 23: A uniform magnetic field of $1.5 \mathrm{~T}$ exists in a cylindrical region of radius $10.0 \mathrm{~cm}$, its direction parallel to the axis along east to west. A wire carrying current of $7.0 \mathrm{~A}$ in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,

Solution. Magnetic field strength, $B=1.5 \mathrm{~T}$

Radius of the cylindrical region, $r=10 \mathrm{~cm}=0.1 \mathrm{~m}$

Current in the wire passing through the cylindrical region, $I=7 \mathrm{~A}$

(a) If the wire intersects the axis, then the length of the wire is the diameter of the cylindrical region.

Thus, $l=2 r=0.2 \mathrm{~m}$

Angle between magnetic field and current, $\theta=90^{\circ}$

Magnetic force acting on the wire is given by the relation,

$F=B \| \sin \theta$

$=1.5 \times 7 \times 0.2 \times \sin 90^{\circ}$

$=2.1 \mathrm{~N}$

Hence, a force of $2.1 \mathrm{~N}$ acts on the wire in a vertically downward direction.

(b) New length of the wire after turning it to the Northeast-Northwest direction can be given as: :

$l_{1}=\frac{l}{\sin \theta}$

Angle between magnetic field and current, $\theta=45^{\circ}$

Force on the wire,

$F=B \|_{1} \sin \theta$

$=B I l$

$=1.5 \times 7 \times 0.2$

$=2.1 \mathrm{~N}$

Hence, a force of $2.1 \mathrm{~N}$ acts vertically downward on the wire. This is independent of angle\thetabecause $/ \sin \theta$ is fixed

(c) The wire is lowered from the axis by distance, $d=6.0 \mathrm{~cm}$

Suppose wire is passing perpendicularly to the axis of cylindrical magnetic field then lowering 6 cm means displacing the wire 6 cm from its initial position towards to end of cross sectional area.





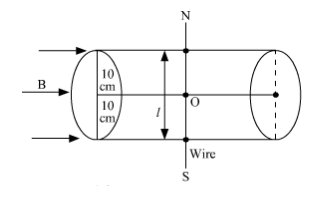
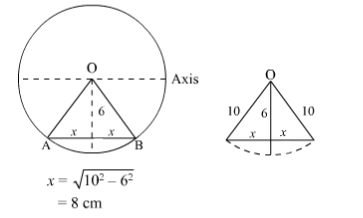
Thus the length of wire in magnetic field will be $16 \mathrm{~cm}$ as $\mathrm{AB}=L=2 x=16 \mathrm{~cm}$

Now the force,

$F=i L B \sin 90^{\circ}$ as the wire will be perpendicular to the magnetic field.

$\mathrm{F}=7 \times 0.16 \times 1.5=1.68 \mathrm{~N}$

The direction will be given by right hand curl rule or screw rule i.e. vertically downwards.

Question $24$ : A uniform magnetic field of $3000 \mathrm{G}$ is established along the positive z-direction. A rectangular loop of sides $10 \mathrm{~cm}$ and $5 \mathrm{~cm}$ carries a current of $12 \mathrm{~A}$. What is the torque on the loop in the different cases shown in Fig. $4.28 ?$ What is the force on each case? Which case corresponds to stable equilibrium?

Solution.



Magnetic field strength, $B=3000 \mathrm{G}=3000 \times 10^{-4} \mathrm{~T}=0.3 \mathrm{~T}$

Length of the rectangular loop, $/=10 \mathrm{~cm}$

Width of the rectangular loop, $b=5 \mathrm{~cm}$

Area of the loop,

$A=1 \times b=10 \times 5=50 \mathrm{~cm}^{2}=50 \times 10^{-4} \mathrm{~m}^{2}$

Current in the loop, $I=12 \mathrm{~A}$

Now, taking the anti-clockwise direction of the current as positive and vise-versa:

(a) Torque, $\vec{\tau}=I \vec{A} \times \vec{B}$

From the given figure, it can be observed that $A$ is normal to the $y-z$ plane and $B$ is directed along the z-axis.

$\therefore \tau=12 \times\left(50 \times 10^{-4}\right) \hat{i} \times 0.3 \hat{k}$

$=-1.8 \times 10^{-2} \hat{j} \mathrm{~N} \mathrm{~m}$

The torque is $1.8 \times 10^{-2} \mathrm{~N} \mathrm{~m}$ along the negative $y$-direction. The force on the loop is zero because the angle between $A$ and $B$ is zero.

(b) This case is similar to case (a). Hence, the answer is the same as (a).

(c) Torque $\tau=I \vec{A} \times \vec{B}$

From the given figure, it can be observed that $A$ is normal to the $x-z$ plane and $B$ is directed along the $z$-axis.

$\therefore \tau=-12 \times\left(50 \times 10^{-4}\right) \hat{j} \times 0.3 \hat{k}$

$=-1.8 \times 10^{-2} \hat{i} \mathrm{Nm}$

The torque is $1.8 \times 10^{-2} \mathrm{~N} \mathrm{~m}$ along the negative $x$ direction and the force is zero.

(d) Magnitude of torque is given as:

$|\tau|=I A B$ $=12 \times 50 \times 10^{-4} \times 0.3$

$=1.8 \times 10^{-2} \mathrm{~N} \mathrm{~m}$

Torque is $1.8 \times 10^{-2} \mathrm{~N} \mathrm{~m}$ at an angle of $240^{\circ}$ with positive $x$ direction. The force is zero.

(e) Torque $\tau=I \vec{A} \times \vec{B}$

$=\left(50 \times 10^{-4} \times 12\right) \hat{k} \times 0.3 \hat{k}$

$=0$

Hence, the torque is zero. The force is also zero.

(f) Torque $\tau=I \vec{A} \times \vec{B}$

$=\left(50 \times 10^{-4} \times 12\right) \hat{k} \times 0.3 \hat{k}$

$=0$

Hence, the torque is zero. The force is also zero.

In case (e), the direction of $I \vec{A}$ and $\vec{B}$ is the same and the angle between them is zero. If displaced, they come back to an equilibrium. Hence, its equilibrium is stable

Whereas, in case (f), the direction of $I \vec{A}$ and $\vec{B}$ is opposite. The angle between them is $180^{\circ} .$ If disturbed, it does not come back to its original position. Hence, its equilibrium is unstable

Question $25$ : A circular coil of 20 turns and radius $10 \mathrm{~cm}$ is placed in a uniform magnetic field of $0.10 \mathrm{~T}$ normal to the plane of the coil. If the current in the coil is $5.0 \mathrm{~A}$, what is the

(a) total torque on the coil,

(b) total force on the coil,

(c) average force on each electron in the coil due to the magnetic field?

(The coil is made of copper wire of cross-sectional area $10^{-5} \mathrm{~m}^{2}$, and the free electron density in copper is given to be about $10^{29} \mathrm{~m}^{-3}$.)

Solution. Number of turns on the circular coil, $n=20$

Radius of the coil, $r=10 \mathrm{~cm}=0.1 \mathrm{~m}$

Magnetic field strength, $B=0.10 \mathrm{~T}$

Current in the coil, I = 5.0 A

(a) The total torque on the coil is zero because the field is uniform.

(b) The total force on the coil is zero because the field is uniform.

(b) The total force on the coil is zero because the field is uniform.

(c) Crocacect nf conner coil $A=10^{-5} \mathrm{~m}^{2}$

Number of free electrons per cubic meter in copper, $N=10^{29} / \mathrm{m}^{3}$

Charge on the electron, $e=1.6 \times 10^{-19} \mathrm{C}$

Magnetic force, $F=\operatorname{Bev}_{d}$

Where,

$v_{d}=$ Drift velocity of electrons

$=\frac{I}{N e A}$

$\therefore F=\frac{B e I}{N e A}$

$=\frac{0.10 \times 5.0}{10^{29} \times 10^{-5}}=5 \times 10^{-25} \mathrm{~N}$

Hence, the average force on each electron is $5 \times 10^{-25} \mathrm{~N}$.

Question 26: A solenoid $60 \mathrm{~cm}$ long and of radius $4.0 \mathrm{~cm}$ has 3 layers of windings of 300 turns each. A $2.0 \mathrm{~cm}$ long wire of mass $2.5 \mathrm{~g}$ lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of $6.0 \mathrm{~A}$ in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? $\mathrm{g}=9.8 \mathrm{~m} \mathrm{~s}^{-2}$

Solution. Length of the solenoid, $L=60 \mathrm{~cm}=0.6 \mathrm{~m}$

Radius of the solenoid, $r=4.0 \mathrm{~cm}=0.04 \mathrm{~m}$

It is given that there are 3 layers of windings of 300 turns each.

$\therefore$ Total number of turns, $n=3 \times 300=900$

Length of the wire, $l=2 \mathrm{~cm}=0.02 \mathrm{~m}$

Mass of the wire, $m=2.5 \mathrm{~g}=2.5 \times 10^{-3} \mathrm{~kg}$

Current flowing through the wire, $i=6 \mathrm{~A}$

Acceleration due to gravity, $\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^{2}$

Magnetic field produced inside the solenoid, $B=\frac{\mu_{0} n I}{L}$

Where,

$\mu_{0}=$ Permeability of free space $=4 \pi \times 10^{-7} \mathrm{~T} \mathrm{~m} \mathrm{~A}^{-1}$

$I=$ Current flowing through the windings of the solenoid

Magnetic force is given by the relation,

$F=$ Bil

$=\frac{\mu_{0} n I}{L} i l$ Also, the force on the wire is equal to the weight of the wire.

$\therefore m g=\frac{\mu_{0} n I i l}{L}$

$I=\frac{m \mathrm{~g} L}{\mu_{0} n i l}$

$=\frac{2.5 \times 10^{-3} \times 9.8 \times 0.6}{4 \pi \times 10^{-7} \times 900 \times 0.02 \times 6}=108 \mathrm{~A}$

Hence, the current flowing through the solenoid is $108 \mathrm{~A}$.

Question 27: A galvanometer coil has a resistance of $12 \Omega$ and the metre shows full scale deflection for a current of $3 \mathrm{~mA}$. How will you convert the metre into a voltmeter of range 0 to $18 \mathrm{~V}$ ?

Solution. Resistance of the galvanometer coil, $G=12 \Omega$

Current for which there is full scale deflection, $I_{\mathrm{g}}=3 \mathrm{~mA}=3 \times 10^{-3} \mathrm{~A}$

Range of the voltmeter is 0, which needs to be converted to $18 \mathrm{~V}$.

$\therefore V=18 \mathrm{~V}$

Let a resistor of resistance $R$ be connected in series with the galvanometer to convert it into a voltmeter. This resistance is given as:

$R=\frac{V}{I_{\mathrm{g}}}-\mathrm{G}$

$=\frac{18}{3 \times 10^{-3}}-12=6000-12=5988 \Omega$

Hence, a resistor of resistance $5988 \Omega$ is to be connected in series with the galvanometer.

Question 28: A galvanometer coil has a resistance of $15 \Omega$ and the metre shows full scale deflection for a current of $4 \mathrm{~mA}$. How will you convert the metre into an ammeter of range 0 to $6 \mathrm{~A} ?$

Solution. Resistance of the galvanometer coil, $G=15 \Omega$

Current for which the galvanometer shows full scale deflection,

$I_{\mathrm{g}}=4 \mathrm{~mA}=4 \times 10^{-3} \mathrm{~A}$

Range of the ammeter is 0, which needs to be converted to $6 \mathrm{~A}$.

$\therefore$ Current, $l=6 \mathrm{~A}$

A shunt resistor of resistance $S$ is to be connected in parallel with the galvanometer to convert it into an ammeter. The value of $S$ is given as:

$S=\frac{I_{g} G}{I-I_{g}}$

$=\frac{4 \times 10^{-3} \times 15}{6-4 \times 10^{-3}}$

$S=\frac{6 \times 10^{-2}}{6-0.004}=\frac{0.06}{5.996}$

$\approx 0.01 \Omega=10 \mathrm{~m} \Omega$

Hence, a $10 \mathrm{~m} \Omega$ shunt resistor is to be connected in parallel with the galvanometer.

Also Read,

Class 12 Physics Notes Free PDF Download.

Class 12 Physics Book Chapterwise Free PDF Download.

Class 11 Physics Exemplar Chapterwise Free PDF Download.

If you have any Confusion related to NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism PDF then feel free to ask in the comments section down below.

To watch Free Learning Videos on Class 12 Physics by Kota’s top IITan’s Faculties Install the eSaral App