NCERT Solutions for Class 9 Maths chapter 9 Exercise 9.2 - Areas of Parallelograms and Triangles

Download now India's Best Exam Prepration App Class 8-9-10, JEE & NEET
Video Lectures	Live Sessions
Study Material	Tests
Previous Year Paper	Revision

Download now India's Best Exam Prepration App

Class 8-9-10, JEE & NEET

Video Lectures

Live Sessions

Study Material

Tests

Previous Year Paper

Revision

Hey, are you a class 9 Student and Looking for Ways to Download NCERT Solutions for Class 9 Maths chapter 9 Exercise 9.2? If Yes then you are at the right place.

Here we have listed Class 9 maths chapter 9 exercise 9.2 solutions in PDF that is prepared by Kota’s top IITian’s Faculties by keeping Simplicity in mind.

If you want to score high in your class 9 Maths Exam then it is very important for you to have a good knowledge of all the important topics, so to learn and practice those topics you can use eSaral NCERT Solutions.

In this article, we have listed NCERT Solutions for Class 9 Maths chapter 9 Exercise 9.2 that you can download to start your preparations anytime.

India's Best Exam Preparation for Class 9th - Download Now

So, without wasting more time Let’s start.

Download The PDF of NCERT Solutions for Class 9 Maths chapter 9 Exercise 9.2 "Areas of Parallelograms and Triangles"

Class 9 maths chapter 9 exercise 9.2 solutions Image 2

So, that’s all from this article. I hope you enjoyed this post. If you found this article helpful then please share it with other students.

India's Best Exam Preparation for Class 9th - Download Now

Q1. In fig, $\mathrm{ABCD}$ is a parallelogram, $\mathrm{AE} \perp \mathrm{DC}$ and $\mathrm{CF} \perp \mathrm{AD}$. If $\mathrm{AB}=16 \mathrm{~cm}, \mathrm{AE}=8 \mathrm{~cm}$ and $\mathrm{CF}=10 \mathrm{~cm}$, find $\mathrm{AD}$.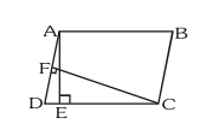

Q2. If $\mathrm{E}, \mathrm{F}, \mathrm{G}$ and $\mathrm{H}$ are respectively the mid-points of the sides of a parallelogram $\mathrm{ABCD}$, show that ar (EFGH) $=\frac{1}{2}$ ar $(\mathrm{ABCD})$.

Q3. $\mathrm{P}$ and $\mathrm{Q}$ are any two points lying on the sides $\mathrm{DC}$ and $\mathrm{AD}$ respectively of a parallelogram $\mathrm{ABCD}$. Show that ar $(\mathrm{APB})=\operatorname{ar}(\mathrm{BQC})$.

Q4. In figure, $\mathrm{P}$ is point in interior of a parallelogram $\mathrm{ABCD}$. Show that:
(i) ar ( $\triangle \mathrm{APB})+\operatorname{ar}(\triangle \mathrm{PCD})$
$=\frac{1}{2} \operatorname{ar}\left(\|^{\mathrm{gm}} \mathrm{ABCD}\right)$
(ii) ar ( $\triangle \mathrm{APD})+$ ar $(\Delta \mathrm{PBC})$
$=\operatorname{ar}(\Delta \mathrm{APB})+\operatorname{ar}(\Delta \mathrm{PCD})$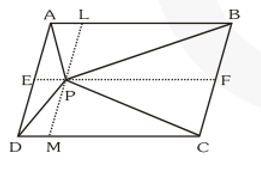

Q5. In fig, PQRS and ABRS are parallelograms and $\mathrm{X}$ is any point on side BR. Show that:
(i) $\operatorname{ar}(\mathrm{PQRS})=\operatorname{ar}(\mathrm{ABRS})$
(ii) $\operatorname{ar}(\mathrm{AX} \mathrm{S})=\frac{1}{2}$ ar $(\mathrm{PQRS})$

Q6. A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points $\mathrm{P}$ and $\mathrm{Q} .$ In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?

Also Read,