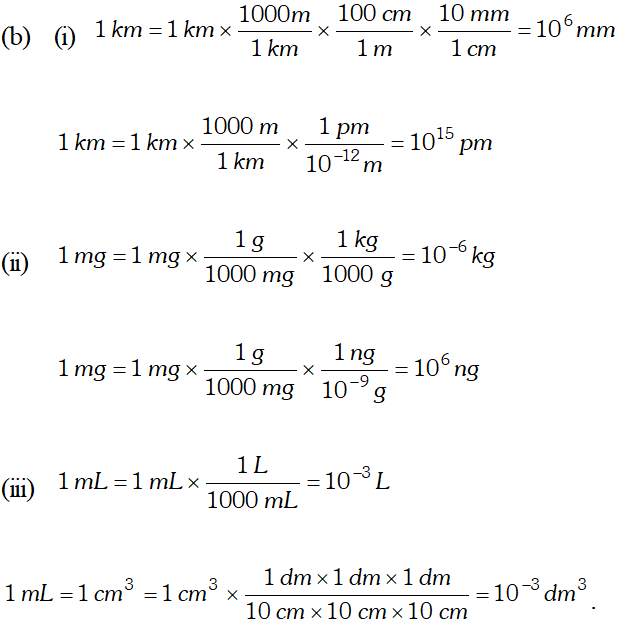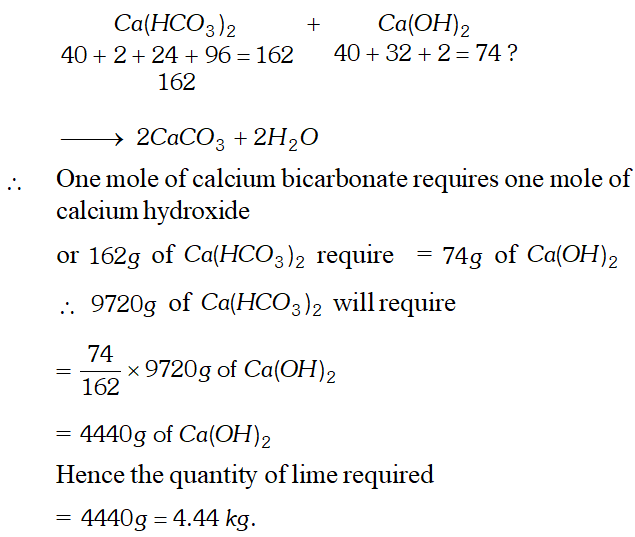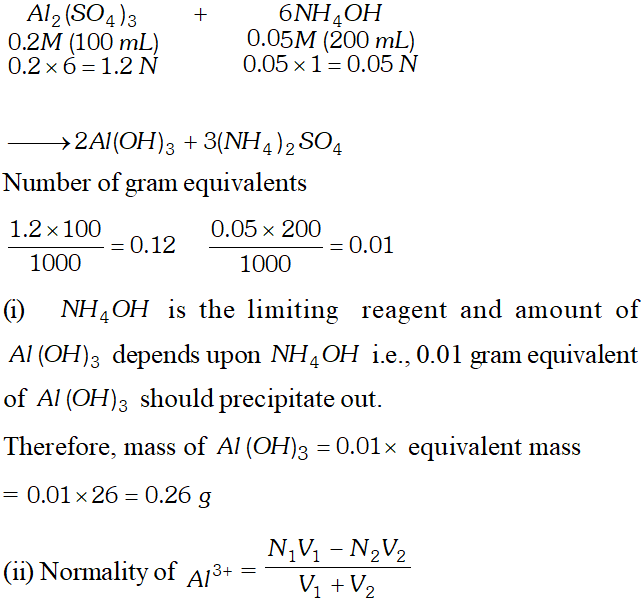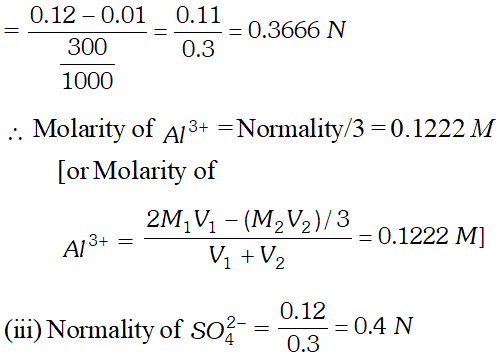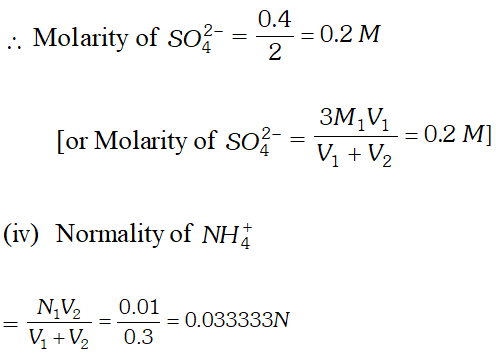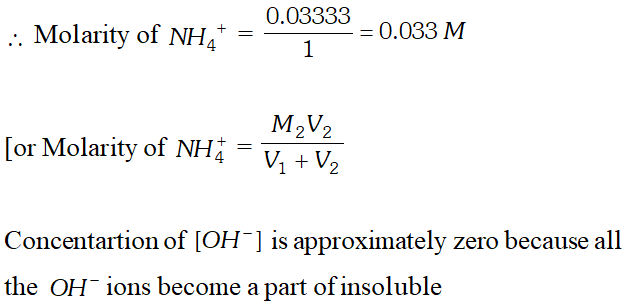Get important solved numericals on Mole Concept for Class 11 and various exams. View the Important Question bank for Class 11 & 12 Chemistry complete syllabus.
These important questions will play significant role in clearing concepts of Chemistry. This question bank is designed keeping NCERT in mind and the questions are updated with respect to upcoming Board exams. You will get here all the important questions and solved numericals for class 11 & 12 chemistry along with Mole Concepts. Learn all important tricks related to Mole Concept with these numericals and access notes too for Class 11 and 12 topics. Click Here for Detailed Chapter-wise Notes of Chemistry for Class 11th, JEE & NEET. You can access free study material for all three subject’s Physics, Chemistry and Mathematics. Click Here for Detailed Notes of any chapter. eSaral provides you complete edge to prepare for Board and Competitive Exams like JEE, NEET, BITSAT, etc. We have transformed classroom in such a way that a student can study anytime anywhere. With the help of AI we have made the learning Personalized, adaptive and accessible for each and every one. Visit eSaral Website to download or view free study material for JEE & NEET. Also get to know about the strategies to Crack Exam in limited time period. Q. What is the SI unit of mass ? How is it defined ? [NCERT]
Ans. The S.I. unit of mass is kilogram.
Mass is defined as the amount of matter present in substance. The unit of mass kilogram is defined as equal to the mass of the international prototype of the kilogram.
Q. Express the following in S.I. base units using power of 10 notation. (example $\left.2.54 \mathrm{mm}=2.54 \times 10^{-3} \mathrm{m}\right)$ (i) $1.35 \mathrm{mm}$ (ii) 1 day (iii) $6.45 \mathrm{mL}$ (iv) $48 \mu g$ (microgram) (v) 0.0426 inches [NCERT]
Ans. (i) $1.35 m m=1.35 \times 10^{-3} \mathrm{m}$ (ii) 1 day $=24 \times 60 \times 60 s=86400 s=8.64 \times 10^{4} s$ (iii) $6.45 \times 10^{-6} \mathrm{m}^{3}\left[\because 1 \mathrm{mL}=10^{-6} \mathrm{m}^{3}\right]$ (iv) $48 \mu g=48 \times 10^{-6} g=4.8 \times 10^{-5} g$ 0.0426 inches (v) $\quad$ linch $=2.54 \times 10^{-2} \mathrm{m}$ \[ =2.54 \times 10^{-2} \mathrm{m} \times 0.0426=1.082 \times 10^{-3} \mathrm{m} \]
Q. When $4.2 \mathrm{g}$ of $\mathrm{NaHCO}_{3}$ is added to solution of $\mathrm{CH}_{3} \mathrm{COOH}$ (acetic acid) weighing $10.0 \mathrm{g},$ it is observed that $2.2 \mathrm{g}$ of $\mathrm{CO}_{2}$ is released into atmosphere. The residue left is found to weigh $12.0 \mathrm{g}$. Show that the observations are in agreement with the law of conservation of mass. $\quad$ [NCERT]
Ans. 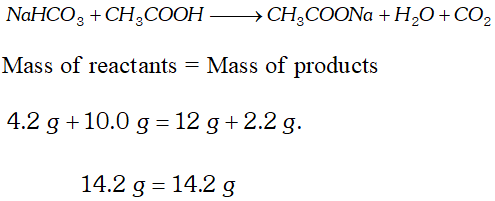 These observations are in agreement with law of conservation of mass.
These observations are in agreement with law of conservation of mass. Q. Define Avogadro’s law.
Ans. Avogadro’s Law : Equal volume of all gases under similar conditions of temperature and pressure contain equal number of molecules.
Q. Give two examples of molecules having molecular formula same as empirical formula
Ans. $\mathrm{CO}_{2}, \quad \mathrm{CH}_{4}$
Q. What is a limiting reactant ? What is its significance during stoichiometric calculations ?
Ans. The limiting reactant is that reactant which is present in minimum amount as required by the stoichiometry of the balanced equation. Since the limiting reactant is completely consumed during the reaction, all the stoichiometric calculations are done keeping the amount of limiting reactant in mind.
Q. Chlorine is prepared according to the reaction : $4 H C l(a q)+M n O_{2}(s) \longrightarrow 2 H_{2} O(l)+M n C l_{2}(a q)+C l_{2}(g)$ How many grams of $H C l$ react with $5.0 \mathrm{g}$ of manganese dioxide? (At. mass of $M n=55$ ). [NCERT]
Ans. According to equation mole ratio of $H C l: M n O_{2}=4: 1$ and mass ratio is $36.5 \times 4: 87=146: 87$ $\therefore \quad H C l$ required in $g=\frac{146}{87} \times 5=8.39 \mathrm{g}$
Q. What is the Concentration of sugar $\left(C_{12} H_{22} O_{11}\right)$ in $\operatorname{mol} L^{-1}$ if its $20 \mathrm{g}$ are dissolved in enough water to make a final volume upto $2 L ?$ [NCERT]
Ans. Molarity of solution $\left(\mathrm{mol} L^{-1}\right)$ $=\frac{\text { Mass of solute }(g)}{\mathrm{M} . \text { mass }} \times \frac{1000}{V \mathrm{inmL}}$ Conc. of sugar $=\frac{20}{342} \times \frac{1000}{2000}=0.0292 \mathrm{mol} \mathrm{L}^{-1}$
Q. Calculate the molality of ethanol in water in which the mole fraction of ethanol is 0.040. [NCERT]
Ans. $X_{\text {ethonol }}=0.040 ; X_{H_{2} O}=0.960$ Molality ( $m)$ $=\frac{1000 \times X_{\text {eth }}}{X_{H_{2} O} \times G M M_{\left(H_{2} O\right)}}=\frac{1000 \times 0.040}{0.96 \times 18}=2.315 m$
Q. If $6.023 \times 10^{23}$ molecules of $N_{2}$ react completely with $H_{2}$ according to the equation: $N_{2}(g)+3 H_{2}(g) \longrightarrow 2 N H_{3}(g)$ Calculate the number of molecules of $N H_{3}$ formed.
Ans. $N_{2}(g)+3 H_{2}(g) \longrightarrow 2 N H_{3}(g)$ $6.023 \times 10^{23}$ molecules of $N_{2}$ react completely with $H_{2}$ to save $2 \times 6.023 \times 10^{23}$ molecules $=1.204 \times 10^{24}$ molecules.
Q. Pressure is determined as force per unit area of the surface. The S.I. unit of pressure, pascal, is as shown below : $1 P a=1 N m^{-2}$ If mass of air at sea level is $1034 g \mathrm{cm}^{-2}$ calculate the pressure in pascal. [NCERT]
Ans. Pressure is the force (i.e., weight) acting per unit area
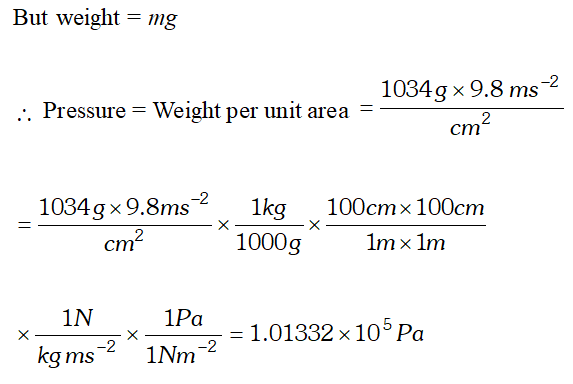
Q. Express the result of the following calculation to the appropriate number of significant digits. $816 \times 0.02456+215.67$ [NCERT]
Ans. $816 \times 0.02456=20.0$ Product rounded off to 3 significant figures because the least number of significant figures in this multiplication is three.
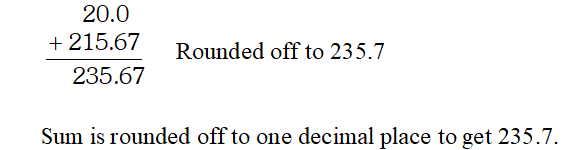
Q. Express the following numbers of four significant figures: (i) 5.607892 (ii) 32.392800 (iii) $1.78986 \times 10^{3}$ (iv) 0.007837 [NCERT]
Ans. (i) 5.608 (ii) 32.39 (iii) $1.790 \times 10^{3}$ (iv) $7.837 \times 10^{-3}$
Q. Express the following number to three significant figures: . (i) $6.022 \times 10^{23}$ (ii) 5.359 (iii) 0.04597 (iv) 34.216 [NCERT]
Ans. (i) The last digit to be retained is 2 and the digit to be dropped is 2 which is less than $5 .$ The result will be expressed as $6.02 \times 10^{23}$ (ii) In this case the last digit to be retained is 5 and the digit to be dropped is $9,$ which is greater than $5 .$ Hence, the last digit to be retained is increased by one. The number will be written as 5.36. (iii) The three digits to be retained in this case are $4,5$ and $9 .$ The digit 7 is to be dropped which is greater than $5 .$ Hence, the last digit to be retained will therefore be increased by one. The number will be rounded off to three significant digits as 0.0460 (iv) In this case the digits 1 and 6 will be dropped. since, the digit following the last digit to be retained is $1,$ the last digit will be kept unchanged and the number is written as $34.2 .$
Q. Calculate the atomic mass (average) of chlorine using the following data :
 [NCERT]
[NCERT] Ans. 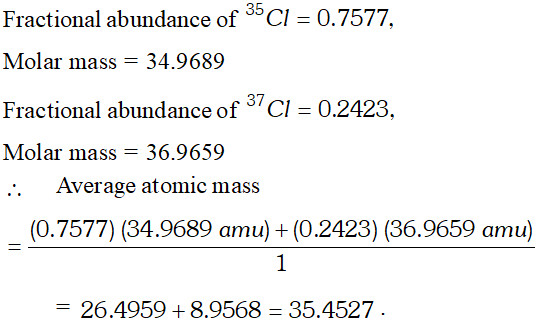
Q. Which one of the following will have largest number of atoms? (i) $1 g A u(s)$ (ii) $1 g N a(s)$ (iii) $1 g L i(s)$ (iv) $1 g C l_{2}(g)$ [at. mass $: A u 197, N a=23, \quad L i=7, \quad C l=35.5]$
Ans. No. of atoms can be calculated as: (i) $1 g A u=\frac{1}{197} \times 6.022 \times 10^{23}=\frac{6.022}{197} \times 10^{23}$ (ii) $\quad 1 g N a=\frac{6.022}{23} \times 10^{23}$ (iii) $1 g L i=\frac{6.022 \times 10^{23}}{7}$ (iv) $1 g C l_{2}=\frac{2 \times 6.022 \times 10^{23}}{71}=\frac{6.022 \times 10^{23}}{35.5}$ It is clear that contains largest number of atoms.
Q. Define the following : (iii) Molar mass (i) Average atomic mass (ii) Mole (iv) Unit factor (v) Molarity (vi) Precision and accuracy. [NCERT]
Ans. (i) Average atomic mass : It is defined as average of the mass of all of the atoms of an elements, e.g., average atomic mass of is 35.5 u. (ii) Mole is defined as amount of substance that contains as many atoms, molecules and particles as there are atoms in exactly 0.012 kg of Carbon-12 isotope. (iii) Molar mass : It is mass of 1 mole of substance which contains $6.022 \times 10^{23}$ particles. (iv) Unit factor : The factor which is used to convert one unit into another is called Unit factor. (v) Molarity : It is defined as number of moles of solute dissolved per litre of solution. (vi) Precision and accuracy : Precision means how closely the experimental measurements agree with another. Accuracy means how close the experimental measurements and exact values are with each other.
Q. In commercial manufacture of $H N O_{3},$ how many moles of $\mathrm{NO}_{2}$ produce $7.33 \mathrm{mol} \mathrm{HNO}_{3}$ in the reaction? $3 \mathrm{NO}_{2}(g)+H_{2} \mathrm{O}(l) \longrightarrow 2 \mathrm{HNO}_{3}(a q)+\mathrm{NO}(g)$ [NCERT]
Ans. $3 \mathrm{NO}_{2}(g)+\mathrm{H}_{2} \mathrm{O}(l) \longrightarrow 2 \mathrm{HNO}_{3}(a q)+\mathrm{NO}(g)$ 2 moles of $H N O_{3}$ need 3 moles of $N O_{2}$ 7.33 mole of $\mathrm{HNO}_{3}$ need $\frac{3}{2} \times 7.33=\frac{21.99}{2}=10.995$ moles of $\mathrm{NO}_{2}$
Q. Use the data given in the following table to calculate the molar mass of naturally occurring argon :
 [NCERT]
[NCERT] Ans. Average atomic mass

Q. How many moles and how many grams of $N a C l$ are present in $250 \mathrm{cm}^{3}$ of $0.50 \mathrm{M} \mathrm{NaCl}$ solution? [ Atomic weight of $N a=$ $23 \mathrm{u}, C l=35.5 \mathrm{u}] \quad \quad$ [NCERT]
Ans. $M=n \times \frac{1000}{\text { Vol. of solution in } \mathrm{cm}^{3}} \Rightarrow 0.50=n \times \frac{1000}{250}$ $\Rightarrow n=0.125 \mathrm{mol}$ Amount of $N a C l=n \times M \cdot w t .=0.125 \times 58.5=7.30 \mathrm{g}$
Q. Potassium bromide $K B r$ contains $32.9 \%$ potassium by mass. If $6.4 \mathrm{g}$ of bromine reacts with $3.60 \mathrm{g}$ of $K,$ calculate the number of moles of $^{c} K^{\prime}$ which combine with bromine to form $K B r$ [NCERT]
Ans. $32.9 \mathrm{g}$ of $\mathrm{K}$ combines with $67.1 \mathrm{g}$ of $\mathrm{Br}$ $3.60 \mathrm{g}$ of $\mathrm{K}$ combines with $\frac{67.1}{32.9} \times 3.60=\frac{241.56}{32.9}=7.342 \mathrm{g}$ since we have $6.4 \mathrm{g}$ of bromine, it means $B r_{2}$ is limiting reactant. Number of moles of $B r_{2}=\frac{6.4 \mathrm{g}}{160}=0.04$ moles $2 K+B r_{2} \longrightarrow 2 K B r$ mole of $B r_{2}$ reacts with 2 moles of Potassium to form $K B r$ 0.04 mole of $B r_{2}$ will react with $2 \times 0.04$ moles of $K$ to form $K B r$ $=0.08$ moles $=8 \times 10^{-2}$ moles of $K$
Q. Calculate the number of atoms in each of the following: (i) 52 moles of $A r$ (iii) $52 g$ of $H e$ (ii) $52 u$ of $H e$ [NCERT]
Ans. (i) Number of atoms of $^{\prime} A r^{\prime}=52 \times 6.02 \times 10^{23}=3.132 \times 10^{25}$ atoms. (ii) 1 atom of He has a mass of 4 u. Number of atoms of ' $^{\prime} H e^{\prime}=\frac{52}{4}=13$ atoms. (iii) Number of moles of ' $\mathrm{He}^{\prime}=\frac{52}{4}=13$ moles $\therefore$ Number of atoms of $^{\prime} H e^{\prime}=13 \times 6.023 \times 10^{23}=7.826 \times 10^{24}$ atoms.
Q. Chlorophyll, the green colouring material of plants contains 2.68% of magnesium by mass. Calculate the number of magnesium atoms in 5.00 g of this complex. [NCERT]
Ans. - Mass of magnesium in $5.00 \mathrm{g}$ of complex $=\frac{2.68}{100} \times 5.00=0.134 g$ No. of moles of $M g=\frac{0.134}{24}$ atoms of $M g=6.023 \times 10^{23} \times \frac{0.134}{24}=3.36 \times 10^{22}$ atoms
Q. In three moles of ethane $\left(C_{2} H_{6}\right)$ calculate the following: (i) Number of moles of carbon (ii) Number of moles of hydrogen atoms (iii) Number of molecules of ethane.
Ans. (i) 1 mole of $C_{2} H_{6}$ contains 2 moles of carbon $\therefore \quad$ Number of moles of carbon in 3 moles of $C_{2} H_{6}=6$ (ii) 1 mole of $C_{2} H_{6}$ contain 6 mole atoms of hydrogen $\therefore \quad$ Number of moles of hydrogen atoms in 3 mole of $C_{2} H_{6}=3 \times 6=18$ (iii) 1 mole of $C_{2} H_{6}=6.022 \times 10^{23}$ molecules $\therefore \quad$ Number of molecules in 3 mole of $C_{2} H_{6}=3 \times 6.022 \times 10^{23}=1.807 \times 10^{24}$ molecules
Q. Calculate the mass of sodium acetate $\left(\mathrm{CH}_{3} \mathrm{COONa}\right)$ required to make $500 \mathrm{mL}$ of 0.375 molar aqueous solution. Molar mass of sodium acetate is $82.0245 \mathrm{g} \mathrm{mol}^{-1}$
Ans. $-0.375 M$ aqueous solution means that $1000 \mathrm{mL}$ of the solution contain sodium acetate $=0.375$ mole $\therefore \quad 500 \quad \mathrm{mL}$ of the solution should contain sodium acetate $=\frac{0.375}{2}$ mole Molar mass of sodium acetate $=82.0245 \mathrm{g} \mathrm{mol}^{-1}$ $\therefore\ Mass of sodium acetate acquired $=\frac{0.375}{2}$ mole $\times 82.0245 \mathrm{g} \mathrm{mol}^{-1}=15.380 \mathrm{g}$
Q. - How much copper can be obtained from $100 \mathrm{g}$ of copper sulphate $\left(C u S O_{4}\right) ?$ [Atomic mass of $C u=63.5$ amu]. [NCERT]
Ans. I mole of $\mathrm{CuSO}_{4}$ contains 1 mole $(1 \mathrm{gatom})$ of $^{c} \mathrm{Cu}^{\prime}$ $\mathrm{CuSO}_{4}=63.5+32+4 \times 16=159.5 \mathrm{gmol}^{-1}$ Thus, $\mathrm{Cu}$ that can be obtained from $159.5 \mathrm{g}$ of $\mathrm{CuSO}_{4}=63.5 \mathrm{g}$ $\therefore \quad \mathrm{Cu}$ that can be obtained from $100 \mathrm{g}$ of $\mathrm{CuSO}_{4}=\frac{63.5}{159.5} \times 100 \mathrm{g}=39.81 \mathrm{g}$ Molar mass of
Q. Find out volume of the following at $S . T . P .$ (i) $14 \mathrm{g}$ of nitrogen (ii) $6.023 \times 10^{22}$ molecules of ammonia $\left(N H_{3}\right)$ (iii) 0.1 mole of sulphur dioxide $\left(S O_{2}\right)$
Ans. (i) Molecular mass of $N_{2}=14 \times 2=28$ $28 g$ of $N_{2}$ occupy at S.T.P. $=22.4$ litres $\therefore 14 g$ of $N_{2}$ occupy at S.T.P. $=\frac{22.4}{28} \times 14=11.2$ litre. (ii) $6.023 \times 10^{23}$ molecules of $\mathrm{NH}_{3}$ occupy at S.T.P. $=22.4$ litres. $\therefore 6.023 \times 10^{22}$ molecules of $\mathrm{NH}_{3}$ occupy at S.T.P. $=\frac{22.4}{6.023 \times 10^{23}} \times 6.023 \times 10^{22}=2.24 L$ (iii) 1 mole of $S O_{2}$ occupies at S.T.P. $=22.4$ litres $\therefore 0.1 \mathrm{mol}$ of $\mathrm{SO}_{2}$ occupies at S.T.P. $=\frac{22.4}{1} \times 0.1=2.24 L$
Q. Ferric sulphate is a crystalline compound of iron. It is used in water and sewage treatment to help the removal of suspended impurities. Calculate the mass percentage of iron, sulphur and oxygen in the compound. [NCERT]
Ans. The formula of the compound is $F e_{2}\left(S O_{4}\right)_{3}$
The formula mass $=2 \times 56+3(32+64)=400 u$ $\therefore \quad$ Percentage of iron $=\frac{2 \times 56 \times 100}{400}=28 \%$ \[\begin{array}{l} {\text { Percentage of sulphur }=\frac{3 \times 32 \times 100}{400}=24 \%} \\ {\text { Percentage of oxygen }=\frac{3 \times 64 \times 100}{400}=48 \%} \end{array}\] Q. Calculate the mass percent of different elements present in sodium sulphate $\left(N a_{2} S O_{4}\right)$. [NCERT]
Ans. Mass of $\mathrm{Na}_{2} \mathrm{SO}_{4}=2 \times 23+32+4 \times 16=46+32+64=142$ Mass $\%$ of $N a=\frac{46}{142} \times 100=32.39$ Mass $\%$ of $S=\frac{32}{142} \times 100=22.54$ Mass $\%$ of $O=\frac{64}{142} \times 100=45.07$
Q. Determine the molecular formula of an oxide of iron in which the mass percent of iron and oxygen are 69.9 and 30.1 respectively. Given that the molar mass of the oxides is $\left.159.8 g \mathrm{mol}^{-1} \text { [ Atomic mass: } \mathrm{Fe}=55.85, O=16.00 \mathrm{amu}\right]$ [NCERT]
Ans. 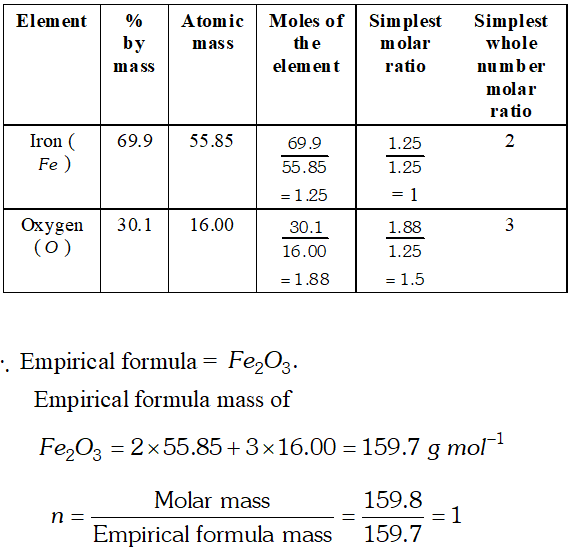 Hence, molecular formula is same as empirical formula, viz.. $\mathrm{Fe}_{2} \mathrm{O}_{3}$
Hence, molecular formula is same as empirical formula, viz.. $\mathrm{Fe}_{2} \mathrm{O}_{3}$ Q. Zinc and hydrochloric acid react according to the reaction: $Z n(s)+2 H C l(a q) \longrightarrow Z n C l_{2}(a q)+H_{2}(g)$ If 0.30 mol $Z n$ are added to hydrochloric acid containing 0.52 mol $\mathrm{HCl},$ how many moles of $\mathrm{H}_{2}$ are produced? Which is the limiting reactant? [NCERT]
Ans. $Z n(s)+2 H C l(a q) \longrightarrow Z n C l_{2}(a q)+H_{2}(g)$ 1 mole of $Z n$ reacts with 2 moles of $H C l$ 0.3 mole of $Z n$ will react with $2 \times 0.30=0.6$ moles of $\mathrm{HCl}$ But we have only 0.52 moles of $H C l,$ therefore, $H C l$ is limiting reactant. 2 moles of $\mathrm{HCl}$ react with 1 mole of $\mathrm{Zn}$ to form 1 mole of $\mathrm{H}_{2}$. 0.52 moles of $\mathrm{HCl}$ react with $\frac{0.52}{2}$ moles of $\mathrm{Zn}$ to form $\frac{0.52}{2}=0.26$ moles of $H_{2}$
Q. In a reaction $A+B_{2} \longrightarrow A B_{2}$ identify the limiting reagent if any in the following reaction mixtures: (i) 300 atoms of $A+200$ molecule of $B$ (ii) $2 \mathrm{mol}$ of $A+3 \mathrm{mol}$ of $B$. (iii) 100 atoms of $A+100$ molecules of $B$ (iv) 5 mol of $A+2.5$ mol of $B$ (v) $2.5 \mathrm{mol}$ of $A+5 \mathrm{mol}$ of $B$ [NCERT]
Ans. According to the equation, 1 mole of Areacts with 1 mole of $B_{2}$ and 1 atom of Areacts with 1 molecule of $B_{2}$ (i) $\quad B$ is limiting reagent because 200 molecules of $B_{2}$ will react with 200 atoms of $A$ and 100 atoms will be left in excess. (ii) $\quad A$ (iii) Both will react completely because it is stoichiometric mixture. No limiting reagent. (iv) $\quad B$ (v) $A$
Q. Reaction of $2 B r^{-}(a q)+C l_{2}(a q) \longrightarrow 2 C l^{-}(a q)+B r_{2}(a q)$ is used for commercial preparation of bromine from its salts. Suppose we have $50.0 \mathrm{mL}$ of 0.060 M solution of $\mathrm{NaBr},$ what volume of $0.050 M$ solution of $C l_{2}$ is needed to react completely with the $B r^{-} ? \quad$ [NCERT]
Ans. 
Q. A solution is prepared by dissolving $18.25 \mathrm{g}$ of $\mathrm{NaOH}$ in distilled water to give $200 \mathrm{cm}^{3}$ of solution. Calculate the molarity of $\mathrm{NaOH}$ in the solution. $\quad$ [Atomic weight of $N a=23, O=16, H=1 u]$ [NCERT]
Ans. $M=\frac{W_{B}}{M_{B}} \times \frac{1000}{\text { Vol. of solution in } \mathrm{cm}^{3}}=\frac{18.25}{40} \times \frac{1000}{200}$ $=2.28 \mathrm{mol} L^{-1}$
Q. Chlorophyll contains $2.68 \%$ of $M g$ by weight. Calculate the number of $M g$ atoms in $2.0 \mathrm{g}$ of Chlorophyll. [ Atomic weight of $M g=24 u]$ [NCERT]
Ans. Amount of $M g$ present in chlorophyll $=$ Mass of chlorophyll $\times \%$ of $M g$ $=2 g \times \frac{2.68}{100}=0.0536 \mathrm{g}$ of $\mathrm{Mg}$ $24 g$ of $M g$ contains $6.023 \times 10^{23}$ atoms $0.0536 g$ of $M g$ contains $\frac{6.023 \times 10^{23}}{24} \times 0.0536=1.345 \times 10^{21}$ atoms
Q. A sample of $\mathrm{NaNO}_{3}$ weighing $0.83 \mathrm{g}$ is placed in a $50 \mathrm{ml}$ flask. What is molarity of solution? [Atomic weight of $N a=$ $23, N=14, O=16 u] \quad \quad$ [NCERT]
Ans. Molecular weight of $\mathrm{NaNO}_{3}=23+14+3 \times 16=23+14+48=85 g \mathrm{mol}^{-1}$ $M=\frac{W_{B}}{M_{B}} \times \frac{1000}{\text { Volume of solution in } m L}$ $=\frac{0.83}{85} \times \frac{1000}{50}=\frac{830}{4250}=\frac{83}{425}=0.1952 M$
Q. In a reaction vessel, $0.184 g$ of $\mathrm{NaOH}$ is required to be added for completing the reaction. How many milli litre of $0.150 M$ NaOH solution should be added for this requirement?
[NCERT]
Ans. $M=\frac{W_{B}}{M_{B}} \times \frac{1000}{\text { Volume of solution }}$ $0.15=\frac{0.184}{40} \times \frac{1000}{\text { Volume of solution }}$ Volume of $\mathrm{NaOH}$ solution $=\frac{184}{40 \times 0.15}=\frac{184}{6}=30.66 \mathrm{mL}$
Q. How many grams of dinitrogen gas are required to completely react with 0.3 gm dihydrogen gas to yield ammonia ? Also calculate the amount of ammonia formed. [NCERT]
Ans. 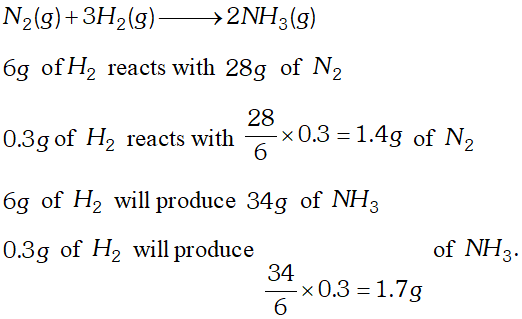
Q. If the density of methanol is $0.793 \mathrm{kg} L^{-1},$ what is its volume needed for making $2.5 L$ of its $0.25 M$ solution $?$ [NCERT]
Ans. Amount of methanol required $m(g)=\frac{\text { Molarity } \times \mathrm{M} . \text { Mass } \times V_{i n} m L}{1000}$ $=\frac{0.25 \times 32 \times 2500}{1000}=20 g$ since, density $=\frac{\text { Mass }}{\text { Volume }}$ $\therefore$ Volume of $\mathrm{CH}_{3} \mathrm{OH}$ required $=\frac{\text { Mass }}{\text { density }}=\frac{20}{0.793}=25.22 \mathrm{mL}$
Q. (i) A sample of $N a O H$ weighing $38 g$ is dissolved in water and the solution is made to $50.0 \mathrm{mL}$ in a volumetric flask. What is the molarity of the resulting solution? (ii) How many moles of $\mathrm{NaOH}$ are contained in $27 \mathrm{mL}$ of $0.15 M N a O H ?$ [NCERT]
Ans. (i) Moles of $\mathrm{NaOH}$ in $50.0 \mathrm{mL}$ solution $=\frac{38}{40}$ $\therefore$ moles of $\mathrm{NaOH}$ in $1.0 \mathrm{L}$ solution \[ =\frac{38}{40} \times \frac{1000}{50}=19 M \] (ii) $1.0 L$ of solution contains moles $=0.15$ $27.0 \mathrm{mL}$ of solution contains moles $=\frac{0.15}{1000} \times 27=4.05 \times 10^{-3} \mathrm{moles}$
Q. A sample of drinking water was found to be severely contaminated with chloroform $\left(\mathrm{CHCl}_{3}\right)$ supposed to be carcinogen. The level of contamination has 15 ppm (by mass) (i) Express this in percent by mass (ii) Determine molality of chloroform in water sample. [NCERT]
Ans. (i) 15 ppm means 15 parts by mass of $\mathrm{CHCl}_{3}$ in $10^{6}$ parts by mass of water Hence, percent by mass \[ =\frac{15}{10^{6}} \times 100=1.5 \times 10^{-3} \% \] (ii) Moles of chloroform $=\frac{15}{119.5}=0.1255$ Hence, molality $(m)$ of $\mathrm{CHCl}_{3}=\frac{0.1255}{10^{6}} \times 10^{3}=1.25 \times 10^{-4} \mathrm{m}$
Q. $500 \mathrm{mL}$ of $0.25 \mathrm{M} \mathrm{Na}_{2} \mathrm{SO}_{4}$ solution is added to an aqueous solution of $15.00 \mathrm{g}$ of $\mathrm{BaCl}_{2}$ resulting in the formation of the white precipitate of insoluble $B a S O_{4} .$ How many moles and how many grams of $B a S O_{4}$ are formed? $\quad$ [At. Wt. of $B a=137 u, S=3 u, O=16 u]$ [NCERT]
Ans. $B a C l_{2}(a q)+N a_{2} S O_{4}(a q) \longrightarrow B a S O_{4}(s)+2 N a C l(a q)$ Number of moles of $N a_{2} \mathrm{SO}_{4}$ $=\left(\frac{500 m L}{1000 m L}\right) \times 0.25 m o l$ $=\frac{0.25}{2}=0.125 \mathrm{mol} \mathrm{Na}_{2} \mathrm{SO}_{4}$ Molar mass of $B a C l_{2}=208.2 \mathrm{g}$ Number of moles of $B a C l_{2}$ $=\frac{15}{208.2}=0.072 \mathrm{mol}$ of $\mathrm{BaCl}_{2}$ 0.072 moles of $B a C l_{2}$ reacts with 0.072 moles of $B a C l_{2}$ to form 0.072 mole of $B a S O_{4}$ Mass of $B a S O_{4}$ formed $=0.072 \times 233.4=16.80 g$ of $B a S O_{4}$
Q. (i) A sample of $N a O H$ weighing 0.38 is dissolved in water and the solution is made to $50.0 \mathrm{cm}^{3}$ in a volumetric flask. What is the molarity of the solution $\quad$ (ii) State and explain law of multiple proportion. [NCERT]
Ans. (i) $\quad M=\frac{W_{B}}{M_{B}} \times \frac{1000}{\text { Volume of solution in } m L}$ \[ =\frac{0.38}{40} \times \frac{1000}{50}=0.19 \mathrm{mol} L^{-1} \] (ii) Law of multiple proportion states whenever two elements reacts to form two or more compounds, the ratio between different weights of one of the elements which combine with fixed weight of another is always simple, e.g., Nitrogen reacts with oxygen to form $\mathrm{NO}$ and $\mathrm{NO}_{2} \cdot$ In $\mathrm{NO}, 14 \mathrm{g}$ of $N$ reacts with $16 \mathrm{g}$ of $\mathrm{O}$ In $\mathrm{NO}_{2} 14 \mathrm{g}$ of $N$ reacts with $32 \mathrm{g}$ of $\mathrm{O} .$ The ratio between weights of oxygen which combine with fixed weight of nitrogen is $16: 32,$ i.e., 1: 2
Q. Express each of the following in
S.I. units :
(i) 93 million miles (this is the distance between the earth and the sun). (ii) 5 feet 2 inches (this is the average height of an Indian female). (iii) 100 miles per hour (this is the typical speed of Rajdhani Express). 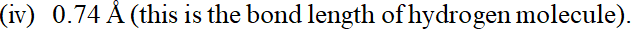 (v) $46^{\circ} \mathrm{C}$ (this is the peak summer temperature in Delhi). (vi) 150 pounds (this is the average weight of an Indian male). [NCERT]
(v) $46^{\circ} \mathrm{C}$ (this is the peak summer temperature in Delhi). (vi) 150 pounds (this is the average weight of an Indian male). [NCERT] Ans. (i) The S.I. unit of distance is metre ( $m$ ) \[ \begin{array}{l} {1 \text { mile }=1.60 \text { kilometre }=1.60 \times 1000 \mathrm{m}} \\ {\text { Unit factor }=\frac{1.60 \times 1000(\mathrm{m})}{1 \mathrm{mile}}=\frac{1.6 \times 10^{3}(\mathrm{m})}{1 \mathrm{mile}}} \end{array} \] 93 millionmiles $=\frac{93 \times 10^{6}(\text { miles }) \times 1.6 \times 10^{3}(\mathrm{m})}{1 \text { mile }}$ $\therefore=93 \times 1.6 \times 10^{9} \mathrm{m}=148.8 \times 10^{9} \mathrm{m}=1.49 \times 10^{11} \mathrm{m}$ (ii) 5 feet 2 inches $=62$ inches \[ \begin{array}{l} {1 \text { inch }=2.54 \times 10^{-2} \mathrm{m}} \\ {\text { Unit factor }=\frac{2.54 \times 10^{-2}(\mathrm{m})}{1 \mathrm{inch}}} \\ {62 \text { inches }=\frac{62(\text { inches }) \times 2.54 \times 10^{-2} \mathrm{m}}{1 \mathrm{inch}}} \\ {=62 \times 2.54 \times 10^{-2} \mathrm{m}} \\ {=157.48 \times 10^{-2} \mathrm{m}=1.57 \mathrm{m}} \end{array} \] (iii) 1 mile $=1.60 \mathrm{km}=1.60 \times 10^{3} \mathrm{m}$ \[ \begin{array}{l} {\text { Unit factor }=\frac{1.60 \times 10^{3} \mathrm{m}}{1 \mathrm{mile}}} \\ {1 \mathrm{hr}=60 \times 60 \mathrm{s}=3.6 \times 10^{3} \mathrm{s}} \\ {\text { Unit factor }=\frac{3.6 \times 10^{3} \mathrm{s}}{1 \mathrm{hr}}} \end{array} \] $\therefore \quad$ Speed $=\frac{100 \text { miles }}{h r}$ $=\frac{100 \text { miles }}{h r} \times \frac{1.60 \times 10^{3} \mathrm{m}}{1 \mathrm{mile}} \times \frac{1 \mathrm{hr}}{3.6 \times 10^{3} \mathrm{s}}=44 \mathrm{ms}^{-1}$ (iv) $1 \dot{A}=10^{-10} \mathrm{m}$ \[ \text { Unit factor }=\frac{10^{-10} \mathrm{m}}{1(\hat{A})} \] $\therefore \quad 0.74 \mathrm{A}=\frac{0.74 \hat{A} \times 10^{-10}(m)}{1(\hat{A})}$ \[ =0.74 \times 10^{-10} \mathrm{m} \text { or }=7.4 \times 10^{-11} \mathrm{m} \] (v) $\quad 0^{\circ} \mathrm{C}=273.15 \mathrm{K}$ $\quad 46^{\circ} \mathrm{C}=273.15 \mathrm{K}+46 \mathrm{K}=319.15 \mathrm{K}$ (vi) 1 pound $=454 \times 10^{-3} \mathrm{kg}$ \[ \text { Unit factor }=\frac{454 \times 10^{-3}(k g)}{1(\text { pound })} \] $\begin{aligned} \therefore \quad 150 \text { pound }=\frac{150(\text { pound }) \times 454 \times 10^{-3}(k g)}{1(\text { pound })} & \\=& 150 \times 454 \times 10^{-3} \mathrm{kg}=68.1 \mathrm{kg} \end{aligned}$
Q. Using the unit conversion factors, express the given measurements in the designated units. (i) $25 L$ to $m^{3}$ (ii) $25 g L^{-1}$ to $m g d L^{-1}$ (iii) $1.54 \mathrm{mms}^{-1}$ to $\mathrm{pm} \mu \mathrm{s}^{-1}$ (iv) $2.66 g \mathrm{cm}^{-3}$ to $\mu g \mu m^{-3}$ (v) $4.22 \mathrm{Lh}^{-2}$ to $\mathrm{mLs}^{-1}$ [NCERT]
Ans. (i) Conversion factor $=\frac{\left(10^{-3} \mathrm{m}^{3}\right)}{(1 . L)}$ \[ 25 L=(25 L) \times \frac{\left(10^{-3} m^{3}\right)}{(1 L)}=2.5 \times 10^{-2} m^{3} \] (ii) Conversion factor= $=\frac{(1000 m g)}{(1 g)} \times \frac{(10 d L)}{(1 L)}$ \[ \begin{array}{l} {25 g L^{-1}=(25 g) \times \frac{\left(10^{3} m g\right)}{(1 g)} \times\left(1 L^{-1}\right) \times \frac{\left(10 d L^{-1}\right)}{\left(1 L^{-1}\right)}} \\ {=2.5 \times 10^{3} \mathrm{mg} d L^{-1}} \end{array} \] (iii) Conversion factor $=\frac{\left(10^{9} p m\right)}{(1 m m)} \times \frac{\left(10^{-6} \mu s\right)}{(1 s)}$ \[ \begin{array}{l} {1.54 \mathrm{mm} \mathrm{s}^{-1}=(1.54 \mathrm{mm}) \times \frac{\left(10^{9} \mathrm{pm}\right)}{(1 \mathrm{mm})}\left(1 \mathrm{s}^{-1}\right) \times \frac{\left(10^{-6} \mu \mathrm{s}^{-1}\right)}{\left(1 \mathrm{s}^{-1}\right)}} \\ {=1.54 \times 10^{3} \mathrm{pm} / \mathrm{s}^{-1}} \end{array} \] (iv) Conversion factor $=\frac{\left(10^{6} \mu g\right)}{(1 g)} \times \frac{\left(10^{4} \mu m\right)}{(1 \mathrm{cm})}$ $2.66 g \mathrm{cm}^{-3}=(2.66 g) \times \frac{\left(10^{6} \mu g\right)}{(1 g)} \times\left(\mathrm{cm}^{-3}\right) \frac{\left(10^{4} \mu m\right)^{-3}}{\left(1 \mathrm{cm}^{-3}\right)}$ $=2.66 \times\left(10^{6} \mu g\right) \times\left(10^{-12} \mu m^{-3}\right)$ \[ =2.66 \times 10^{-6} \mu g \mu m^{-3} \] (v) Conversion factor $=\frac{10^{3} m L}{(1 L)} \times \frac{(60 \times 60 \mathrm{s})}{1 h}$ $\quad 4.2 \mathrm{Lh}^{-2}=(4.2 \mathrm{L}) \times \frac{\left(10^{3} \mathrm{mL}\right)}{(1 \mathrm{L})} \times\left(h^{-2}\right) \times \frac{(60 \times 60 \mathrm{s})^{-2}}{\left(h^{-2}\right)}$ $=3.24 \times 10^{-4} \mathrm{mL} s^{-2}$
Q. The following data were obtained when dinitrogen and dioxygen react together to form different compounds :
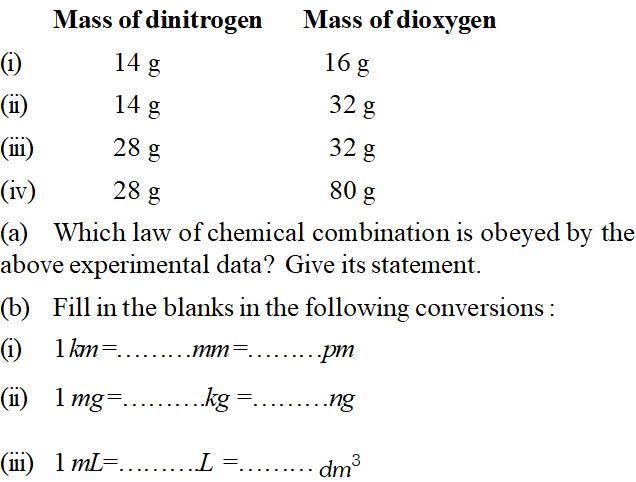 [NCERT]
[NCERT] Ans. (a) Fixing the mass of dinitrogen as 28
g, masses of dioxygen combined will be 32, 64, 32 and 80
g in the given four oxides. These are in the ratio 1 : 2 : 1 : 5 which is a simple number ratio. Hence, the given data obey the law of multiple proportion.
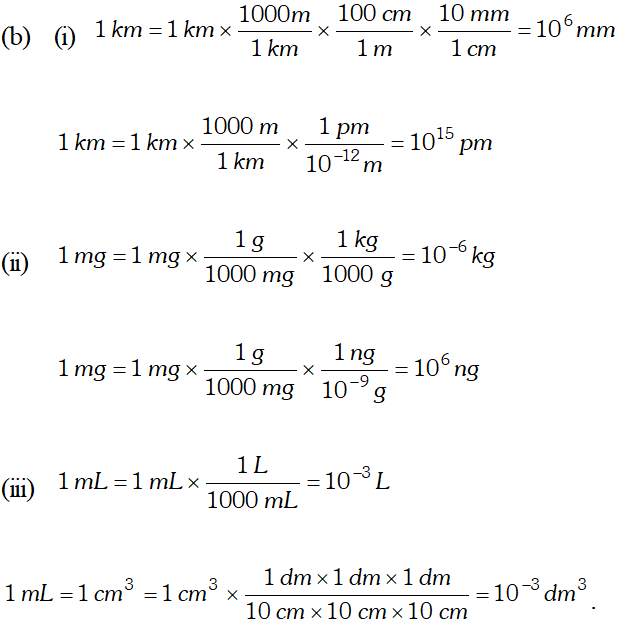
Q. Explain ‘Avogadro’s Number’ and ‘Mole’. What is their importance ? Avogadro’s number may be defined as the number of atoms present in one gram atom of the element or the number of molecules present in one gram molecule of the substance. The amount of the substance containing Avogadro’s number of atoms or molecules is called a mole (or simply written as mol). Thus, a mole is a chemist’s unit of counting particles such as atoms, molecules, ions, electrons, protons etc., which represents a value of $6.022 \times 10^{23}$ A mole of hydrogen atoms means $6.022 \times 10^{23}$ atoms of hydrogen whereas a mole of hydrogen molecules means $6.022 \times 10^{23}$ molecules of hydrogen or $2 \times 6.022 \times 10^{23}$ atoms of hydrogen (because each hydrogen molecule contains 2 atoms of hydrogen). Similarly, a mole of oxygen molecules means $6.022 \times 10^{23}$ molecules of oxygen or $2 \times 6.022 \times 10^{23}$ atoms of oxygen. A mole of sand particles means $6.022 \times 10^{23}$ sand particles. A mole of electrons means $6.022 \times 10^{23}$ electrons and so on.
Ans.
Q. Calculate number of moles in each of the following : (i) $11 \mathrm{g}$ of $\mathrm{CO}_{2}$ (ii) $3.01 \times 10^{22}$ molecules of $\mathrm{CO}_{2}$ (iii) 1.12 litre of $\mathrm{CO}_{2}$ at $\mathrm{S.T.P.}$
Ans. (i) Molecular mass of $C O_{2}$ \[ =(12+2 \times 16)=44 \] $44 \mathrm{g}$ of $\mathrm{CO}_{2}=1 \mathrm{mole}$ of $\mathrm{CO}_{2}$ $11 \mathrm{g}$ of $\mathrm{CO}_{2}=\frac{1}{44} \times 11=0.25 \mathrm{mol}$ (ii) $6.02 \times 10^{23}$ molecules of $\mathrm{CO}_{2}$ $=1$ mole of $C O_{2}$ $3.01 \times 10^{22}$ molecules of $\mathrm{CO}_{2}$ $=\frac{1}{6.02 \times 10^{23}} \times 3.01 \times 10^{22}=0.05 \mathrm{mol}$ (iii) 22.4 litres of $\mathrm{CO}_{2}$ at S.T.P. $=1$ mole of $C O_{2}$ 1.12 litres of $\mathrm{CO}_{2}$ at S.T.P. $=\frac{1}{22.4} \times 1.12=0.05 \mathrm{mol}$
Q. Butyric acid contains C, H, O elements. A 4.24 mg sample of butyric acid is completely burnt in oxygen. It gives 8.45 mg of carbon dioxide and 3.46 mg of water. What is the mass percentage of each element ? Determine the empirical and molecular formula of butyric acid if molecular mass of butyric acid is determined to be 88 u. [NCERT]
Ans. Mass of carbon present in $8.45 \mathrm{mg}$ of $\mathrm{CO}_{2}$ $=\frac{8.45 \times 12}{44} m g=2.30 m g$ Percentage of carbon $=\frac{2.30 \times 100}{4.24}=54.24 \%$ Mass of hydrogen in $3.46 \mathrm{mg}$ of $\mathrm{H}_{2} \mathrm{O}$ $=\frac{3.46 \times 2}{18} m g=0.384 m g$ Percentage of hydrogen $=\frac{0.384 \times 100}{4.24}=9.05 \%$ Percentage of oxygen $=100-54.24-9.05=36.71 \%$
Q. A welding fuel contains carbon and hydrogen only. Burning a small sample of it in oxygen gives 3.38 g of carbon dioxide and 0.690 g of water and no other products. 10.0 L of this welding gas at S.T.P. is found to weigh 11.6 g. Calculate : (i) empirical formula, (ii) molar mass, and (iii) molecular formula of welding gas. [NCERT]
Ans. (i) Calculation of empirical formula: Mass of carbon in 3.38 g carbon dioxide $=\frac{12 \times 3.38}{44}=0.922 g$ Mass of hydrogen in 0.690 g of water $=\frac{2 \times 0.690}{18}=0.077 g$ The ratio by mass of $C$ and $H$ in the sample $=0.922: 0.077$ The mole ratio of $C$ and $H$ in the sample $=\frac{0.922}{12}: \frac{0.077}{1}=0.077: 0.077=1: 1$ Thus empirical formula of the gas is $C H$ (ii) Calculation of molar mass: $10.0 \mathrm{L}$ of gas at S.T.P. weighs $=11.6 \mathrm{g}$ $22.4 \mathrm{L}$ of gas at S.T.P. weighs $=\frac{11.6 \times 22.4}{10}=25.98 g$ Thus, molar mass of gas $=25.98 \mathrm{g} \mathrm{mol}^{-1}$ (iii) Calculation of molecular formula: $n=\frac{\text { Molecular mass }}{\text { Empirical formula mass }}=\frac{25.98}{13}=1.998 \approx 2$ Thus, molecular formula is $(C H)_{2}=C_{2} H_{2}$
Q. Naphthalene (moth balls) contains $93.71 \%$ carbon and $6.29 \%$ hydrogen. If its molar mass is $128 g \mathrm{mol}^{-1},$ calculate its molecular formula. [NCERT]
Ans. From the data given it is clear that if we have $100.0 \mathrm{g}$ of naphthalene, there are $93.71 \mathrm{g}$ of $\mathrm{C}$ and $6.29 \mathrm{g}$ of $\mathrm{H.Number}$ of moles of $\mathrm{C}$ and H in $100.0 \mathrm{g}$ sample of naphthalene are $93.71 g C\left(\frac{1 \mathrm{mol} C}{12.0 \mathrm{g} C}\right)=7.80 \mathrm{mol} \mathrm{C}$ $6.29 g H\left(\frac{1 \mathrm{mol} H}{1.00 g H}\right)=6.29 \mathrm{mol} \mathrm{H}$ Mole ratio $=\left(\frac{7.80 \mathrm{mol} \mathrm{C}}{6.29 \mathrm{mol} \mathrm{H}}\right)=\left(\frac{1.24 \mathrm{mol} \mathrm{C}}{1.00 \mathrm{mol} \mathrm{H}}\right)$ Changing the decimal fraction into whole number ratio of $C$ and $H,$ we know $1.24 \cong \frac{5}{4}$ Therefore, the ratio of $C$ to $H$ is Mole ratio $=\frac{5 / 4 \mathrm{mol} \mathrm{C}}{1 \mathrm{mol} \mathrm{H}}=\frac{5 \mathrm{mol} \mathrm{C}}{4 \mathrm{mol} \mathrm{H}}$ The ratio of carbon to hydrogen atoms in naphthalene is 5: 4 giving the empirical formula, $C_{5} H_{4} .$ The ratio of molecular mass to the empirical mass gives the factor with which the empirical formula is multiplied to obtain the molecular formula. $\frac{128 g / m o l \text { of napthalene }}{64.0 g / m o l \text { of } C_{5} H_{4}}=2.00$ Thus, molecular formula of naphthalene is given by empirical formula multiplied by $2,$ i.e. $\left(C_{5} H_{4}\right)_{2}$ or $C_{10} H_{8}$
Q. Calculate the amount of lime $C a(O H)_{2}$ required to remove the hardness of $60,000$ litres of well water containing $16.2 \mathrm{g}$ of calcium bicarbonate per hundred litres. [ Atomic masses $C a=40, \quad C=12, \quad O=16, H=1]$
Ans. (i) Calculation of the weight of calcium bicarbonate present. Wt. of calcium bicarbonate present in 100 litres of well water $=16.2 \mathrm{g}$
Wt. of calcium bicarbonate present in $60,000$ litres of \[ \text { well water }=\frac{16.2}{100} \times 60000 g=9720 g \] (ii) Calculation of the quantity of lime required. The equation involved is: 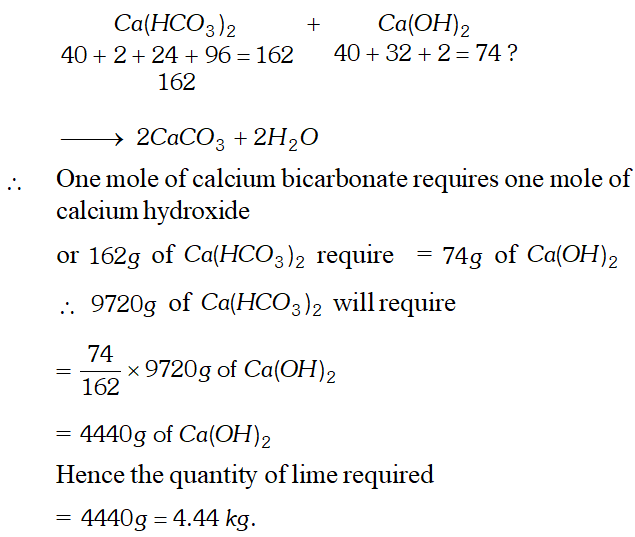
Q. A solution of glucose in water is labelled as $10 \%(\mathrm{w} / \mathrm{w}) .$ The density of the solution is $1.20 g \mathrm{mL}^{-1} .$ Calculate (i) Molality (ii) Molarity, and (iii) Mole fraction of each component in solution.
Ans. $10 \%$ (w/w) solution of glucose means that $10 g$ of glucose is present in $100 g$ of solution or in $90 g$ of water. (i) Calculation of molality \[ \begin{array}{l} {\text { Mass of glucose }=10 g} \\ {\text { Moles of glucose }=\frac{10}{180}=0.0556} \end{array} \] (Molar mass of glucose $=180$ ) Mass of water $=90 g$ Molality $=\frac{\text { Moles of glucose }}{\text { Mass of water }} \times 1000$ \[ =\frac{0.0556}{90} \times 1000=0.618 m \] (ii) Calculation of molarity Moles of glucose $=0.0556$ Volume of solution $=\frac{\text { Mass }}{\text { Density }}=\frac{100}{1.20}=83.3 \mathrm{mL}$ Molarity $=\frac{\text { Moles of glucose }}{\text { Vol. of solution }} \times 1000$ $=\frac{0.0556}{83.3} \times 1000=0.667 M$ (iii) Calculation of mole fraction of components \[ \begin{array}{l} {\text { Moles of glucose }=0.0556} \\ {\text { Moles of water }=\frac{90}{18}=5.0} \\ {\text { Total moles }=5.0+0.0556=5.0556} \end{array} \] Mole fraction of glucose $=\frac{0.0556}{5.0556}=0.011$ Mole fraction of water $=\frac{5.0}{5.0556}=0.989$
Q. $100 \mathrm{mL}$ of $0.2 \mathrm{M} \mathrm{Al}_{2}\left(\mathrm{SO}_{4}\right)_{3}$ is mixed with $200 \mathrm{mL}$ of $0.05 M N H_{4} O H .$ Calculate the amount of $A l(O H)_{3}$ precipitated and the molarity and normality of the resulting solution in terms of each ion.
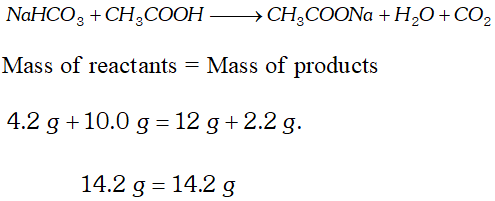 These observations are in agreement with law of conservation of mass.
These observations are in agreement with law of conservation of mass. 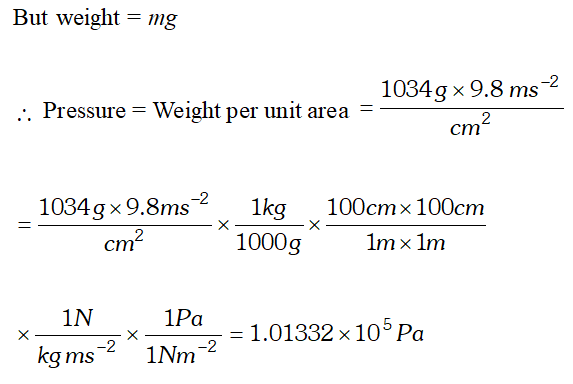
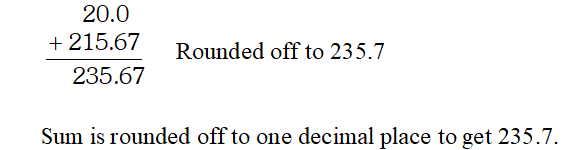
 [NCERT]
[NCERT] 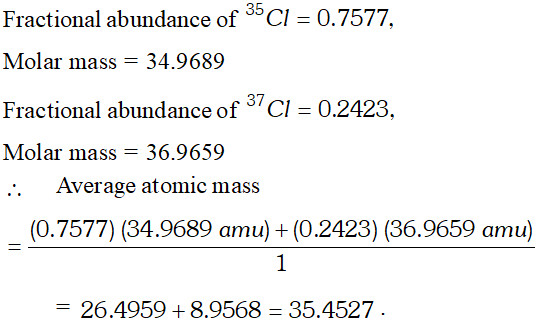
 [NCERT]
[NCERT] 
 Hence, molecular formula is same as empirical formula, viz.. $\mathrm{Fe}_{2} \mathrm{O}_{3}$
Hence, molecular formula is same as empirical formula, viz.. $\mathrm{Fe}_{2} \mathrm{O}_{3}$ 
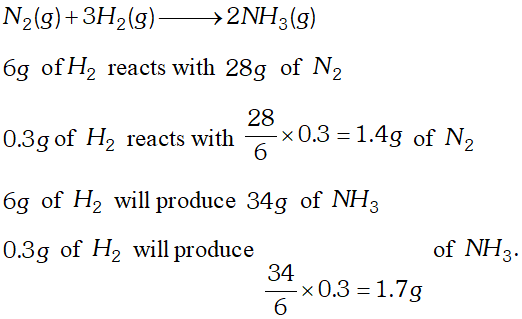
![]() (v) $46^{\circ} \mathrm{C}$ (this is the peak summer temperature in Delhi). (vi) 150 pounds (this is the average weight of an Indian male). [NCERT]
(v) $46^{\circ} \mathrm{C}$ (this is the peak summer temperature in Delhi). (vi) 150 pounds (this is the average weight of an Indian male). [NCERT] 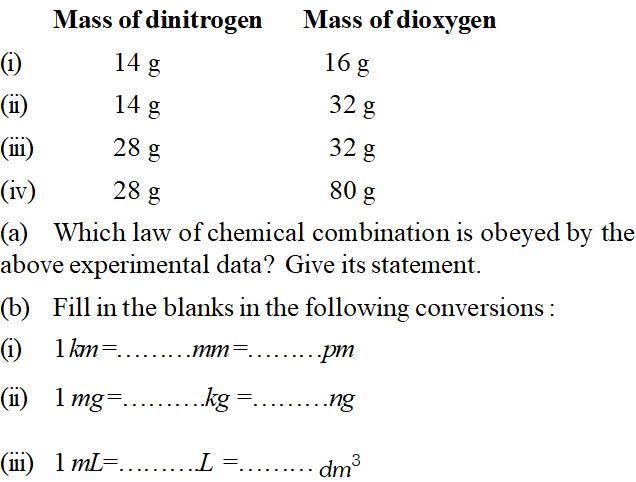 [NCERT]
[NCERT]