Potential Energy of Magnetic Dipole in Magnetic Field || Magnetism Class 12 Physics Notes
JEE Mains & AdvancedPotential Energy of magnetic dipole in a magnetic field is defined as the amount of work done in rotating the dipole from zero potential energy position to any desired position.
A current loop does not experience a net force in a magnetic field. It, however, experiences a torque. This is very similar to the behavior of an electric dipole in an electric field. A current loop, therefore, behaves like a magnetic dipole.
India's Best Exam Preparation for Class 12th - Download Now
Potential Energy of a Bar Magnet in Uniform Magnetic Field
When a bar magnet of dipole moment M is kept in a uniform magnetic field B it experiences a torque $\tau=M B \sin \theta$ which tries to align it parallel to the direction of the field.
If the magnet is to be rotated against this torque work has to be done.
India's Best Exam Preparation for Class 12th - Download Now
The work done in rotating dipole by small-angle d$\theta $ is $d W =\tau d \theta$
Total work done in rotating it from angle $\theta_{1}$ to $\theta_{2}$ is
$\mathrm{W}=\int \mathrm{dW}=\int_{\theta_{1}}^{\theta_{2}} \tau \mathrm{d} \theta=\mathrm{MB} \int_{\theta_{1}}^{\theta_{2}} \sin \theta \mathrm{d} \theta$
$=\operatorname{MB}\left(\cos \theta_{1}-\cos \theta_{2}\right)$
This work done in rotating the magnet is stored inside the magnet as its potential energy.
So U = MB $\left(\cos \theta_{1}-\cos \theta_{2}\right)$
The potential energy of a bar magnet in a magnetic field is defined as work done in rotating it from a direction perpendicular to the field to any given direction.
$U = W _{ \theta }- W _{\frac{\pi}{2}}=- MB \cos \theta=-\overrightarrow{ M } \cdot \overrightarrow{ B }$ 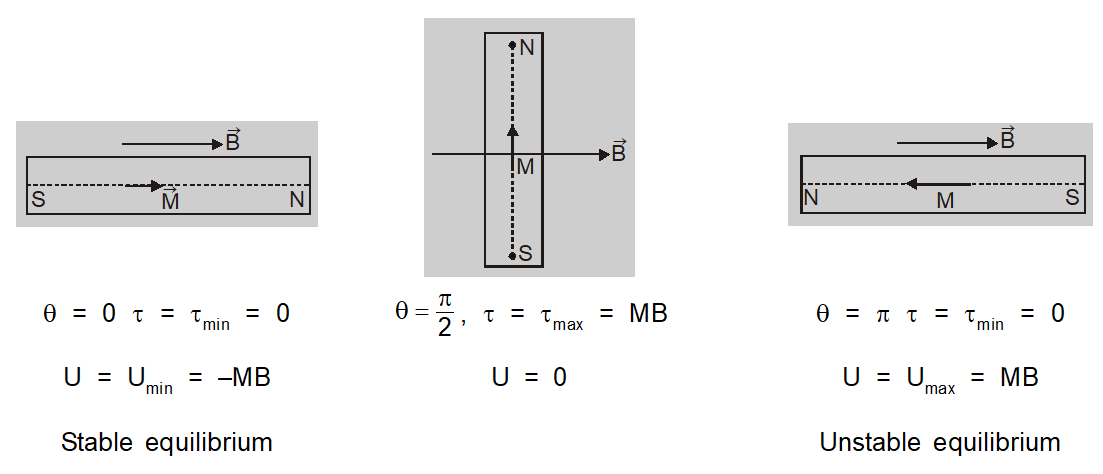
Also Read:
India's Best Exam Preparation for Class 12th - Download Now
About eSaral At eSaral we are offering a complete platform for IIT-JEE & NEET preparation. The main mission behind eSaral is to provide education to each and every student in India by eliminating the Geographic and Economic factors, as a nation’s progress and development depends on the availability of quality education to each and every one. With the blend of education & technology, eSaral team made the learning personalized & adaptive for everyone.
India's Best Exam Preparation for Class 12th - Download Now
For free video lectures and complete study material, Download eSaral APP.
