A block of mass m slides along a floor while a force of magnitude F is applied to it at an angle T as shown in figure.
Question:
. A block of mass m slides along a floor while a force of magnitude F is applied to it at an angle T as shown in figure. The coefficient of kinetic friction is µK. Then, the block's acceleration 'a' is given by : (g is acceleration due to gravity)
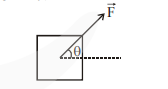
Correct Option: 2,
Solution:
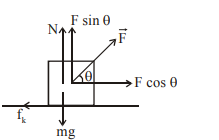
$\mathrm{N}=\mathrm{mg}-\mathrm{f} \sin \theta$
$\mathrm{F} \cos \theta-\mu_{\mathrm{k}} \mathrm{N}=\mathrm{ma}$
$F \cos \theta-\mu_{k}(m g-F \sin \theta)=m a$
$a=\frac{F}{m} \cos \theta-\mu_{K}\left(g-\frac{F}{m} \sin \theta\right)$
