A body is projected vertically upwards from the surface of earth with a velocity sufficient enough to carry it to infinity.

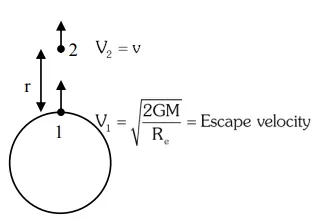
Applying energy conservation from (1) to (2)

$\frac{1}{2} \mathrm{~m} \cdot\left(\frac{2 \mathrm{GM}}{\mathrm{R}_{e}}\right)-\frac{\mathrm{GMm}}{\mathrm{R}_{e}}=\frac{1}{2} \mathrm{mv}^{2}-\frac{\mathrm{GMm}}{\mathrm{R}+\mathrm{r}}$

$\Rightarrow \quad \frac{1}{2} m v^{2}=\frac{G M m}{R+r}$

$\Rightarrow \quad v=\sqrt{\frac{2 G M}{R+r}}=\frac{d r}{d t}$

$\Rightarrow \quad \sqrt{2 G M} \int_{0}^{t} d t=\int_{R_{e}}^{R_{e}+h}(\sqrt{R+r}) d r$

$\sqrt{2 G M} \cdot t=\frac{2}{3}\left[(R+r)^{3 / 2}\right]_{R_{e}}^{R_{e}+h}$

$\mathrm{t}=\frac{2}{3} \sqrt{\frac{\mathrm{R}_{e}^{3}}{2 \mathrm{GM}}}\left[\left(1+\frac{\mathrm{h}}{\mathrm{R}_{e}}\right)^{3 / 2}-1\right]$

$\frac{\mathrm{GM}}{\mathrm{R}_{e}^{2}}=g$

$t=\frac{1}{3} \sqrt{\frac{2 R_{e}}{g}}\left[\left(1+\frac{h}{R_{e}}\right)^{3 / 2}-1\right]$