A circle is inscribed in an equilateral triangle ABC is side 12 cm,

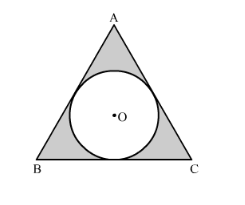
We have to find the area of the shaded portion. We have $\triangle \mathrm{ABC}$ which is an equilateral triangle and $\mathrm{AB}=12 \mathrm{~cm}$.

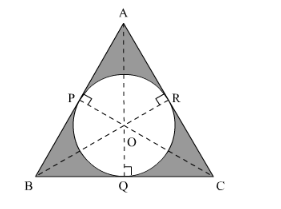
We have O as the incentre and OP, OQ and OR are equal.

So,

$a r(\Delta \mathrm{ABC})=a r(\Delta \mathrm{OAB})+a r(\Delta \mathrm{OBC})+a r(\Delta \mathrm{OCA})$

Thus,

$\frac{\sqrt{3}}{4}(12)^{2}=3\left(\frac{1}{2}(12)(r)\right)$

$r=\frac{36 \sqrt{3}}{18} \mathrm{~cm}$

$=2 \sqrt{3} \mathrm{~cm}$

So area of the shaded region,

$=\operatorname{ar}(\triangle \mathrm{ABC})-$ Area of the circle

$=\frac{\sqrt{3}}{4}(12)^{2}-\frac{22}{7}(2 \sqrt{3})^{2}$

$=(62.35-37.71) \mathrm{cm}^{2}$

$=24.64 \mathrm{~cm}^{2}$