A coin is biased so that the head is 3 times as likely to occur as tail.

Let the probability of getting a tail in the biased coin be x.

$\therefore P(T)=x$

$\Rightarrow P(H)=3 x$

For a biased coin, P (T) + P (H) = 1

$\Rightarrow x+3 x=1$

$\Rightarrow 4 x=1$

$\Rightarrow x=\frac{1}{4}$

$\therefore \mathrm{P}(\mathrm{T})=\frac{1}{4}$ and $\mathrm{P}(\mathrm{H})=\frac{3}{4}$

When the coin is tossed twice, the sample space is {HH, TT, HT, TH}.

Let X be the random variable representing the number of tails.

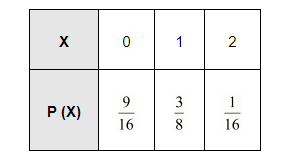
$\therefore \mathrm{P}(\mathrm{X}=0)=\mathrm{P}($ no tail $)=\mathrm{P}(\mathrm{H}) \times \mathrm{P}(\mathrm{H})=\frac{3}{4} \times \frac{3}{4}=\frac{9}{16}$

$P(X=1)=P($ one tail $)=P(\mathrm{HT})+P(\mathrm{TH})$

$=\frac{3}{4} \cdot \frac{1}{4}+\frac{1}{4} \cdot \frac{3}{4}$

$=\frac{3}{16}+\frac{3}{16}$

$=\frac{3}{8}$

$P(X=2)=P$ (two tails) $=P(T T)=\frac{1}{4} \times \frac{1}{4}=\frac{1}{16}$

Therefore, the required probability distribution is as follows.