A current of 1 ampere flows in a series circuit containing

Solution:

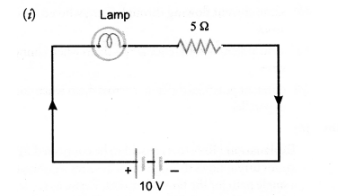
Let $\quad R_{1}=$ resistance of electric lamp.

Total resistance of the ciruit, $R=\left(R_{1}+5\right) \Omega$

Voltage, $\quad \mathrm{V}=10 \mathrm{~V}$

Current, $\quad I=1 \mathrm{~A}$

Using, $\quad V=I R$, we get

$10=1 \times\left(R_{1}+5\right)$ or $R_{1}+5=10$

or $\quad \mathrm{R}_{1}=5 \Omega$

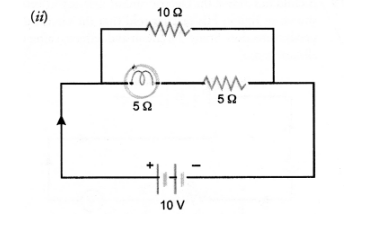
Net resistance of lamp and conductor connected in series = 5 + 5 = 10Ω

Net resistance of the combination oflamp and conductor and resistance 10Ω connected in parallel,

$\frac{1}{R}=\frac{1}{10}+\frac{1}{10}=\frac{1}{5}$ or $R=5 \Omega$

$\therefore$ Current flowing in the circuit, $\mathrm{I}=\frac{\mathrm{V}}{\mathrm{R}}=\frac{10}{5}=2 \mathrm{~A}$

It means 1A current will flow through 10Ω resistance and 1A current will flow through the lamp and conductor of 5Ω resistance. Hence, there is no

change in the current through 5Ω conductor.

Now potential difference across the lamp in case (i)

V = IR = 1 x 5 = 5V

Potential difference across the lamp in case (ii)

V = IR = 1 x 5 = 5V

Hence, there is no change in the potential difference across the lamp.