A diet is to contain at least 80 units of vitamin A and 100 units of minerals.

Let the diet contain $x$ units of food $F_{1}$ and $y$ units of food $F_{2}$. Therefore,

$x \geq 0$ and $y \geq 0$

The given information can be complied in a table as follows.

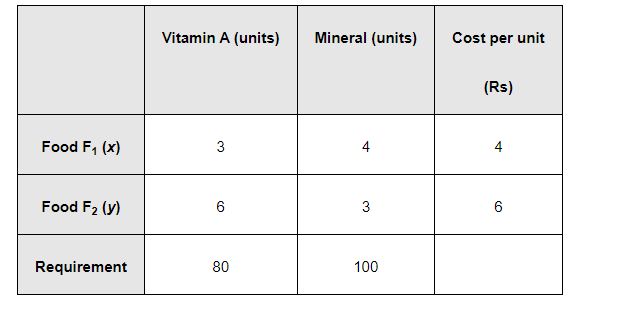
The cost of food $F_{1}$ is Rs 4 per unit and of Food $F_{2}$ is Rs 6 per unit. Therefore, the constraints are

$3 x+6 y \geq 80$

$4 x+3 y \geq 100$

$x, y \geq 0$

Total cost of the diet, $Z=4 x+6 y$

The mathematical formulation of the given problem is

Minimise $Z=4 x+6 y \ldots$                   ...(1)

subject to the constraints,

$3 x+6 y \geq 80 \ldots(2)$

$4 x+3 y \geq 100 \ldots(3)$

$x, y \geq 0 \ldots(4)$

The feasible region determined by the constraints is as follows.

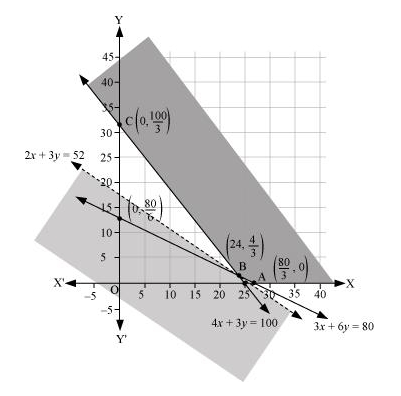
It can be seen that the feasible region is unbounded.

The corner points of the feasible region are $\mathrm{A}\left(\frac{8}{3}, 0\right), \mathrm{B}\left(2, \frac{1}{2}\right)$, and $\mathrm{C}\left(0, \frac{11}{2}\right)$.

The corner points are $\mathrm{A}\left(\frac{80}{3}, 0\right), \mathrm{B}\left(24, \frac{4}{3}\right)$, and $\mathrm{C}\left(0, \frac{100}{3}\right)$.

The values of Z at these corner points are as follows.

As the feasible region is unbounded, therefore, 104 may or may not be the minimum value of Z.

For this, we draw a graph of the inequality, $4 x+6 y<104$ or $2 x+3 y<52$, and check whether the resulting half plane has points in common with the feasible region or not.

It can be seen that the feasible region has no common point with $2 x+3 y<52$

Therefore, the minimum cost of the mixture will be Rs 104 .