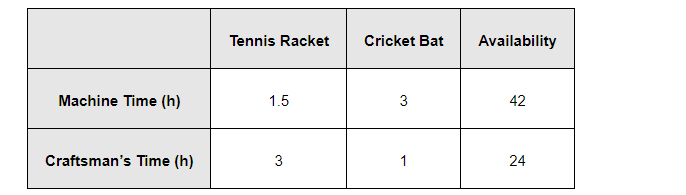
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftsman’s time in its making while a cricket bat takes 3 hour of machine time and 1 hour of craftsman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time.
(ii) What number of rackets and bats must be made if the factory is to work at full capacity?
(ii) If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity.
(i) Let the number of rackets and the number of bats to be made be x and y respectively.
The machine time is not available for more than 42 hours.
$\therefore 1.5 x+3 y \leq 42$ (1)
The craftsman’s time is not available for more than 24 hours.
$\therefore 3 x+y \leq 24$ (2)
The factory is to work at full capacity. Therefore,
$1.5 x+3 y=42$
$3 x+y=24$
On solving these equations, we obtain
x = 4 and y = 12
Thus, 4 rackets and 12 bats must be made.
(i) The given information can be complied in a table as follows.
$\therefore 1.5 x+3 y \leq 42$
$3 x+y \leq 24$
$x, y \geq 0$
The profit on a racket is Rs 20 and on a bat is Rs 10.
$\therefore Z=20 x+10 y$
$3 x+y \leq 24$
$x, y \geq 0$
The profit on a racket is Rs 20 and on a bat is Rs 10.
$\therefore Z=20 x+10 y$
The mathematical formulation of the given problem is
Maximize $Z=20 x+10 y$ ...(1)
subject to the constraints,
$1.5 x+3 y \leq 42 \ldots$ (2)
$3 x+y \leq 24 \ldots$ (3)
$x, y \geq 0 \ldots$ (4)
The feasible region determined by the system of constraints is as follows.
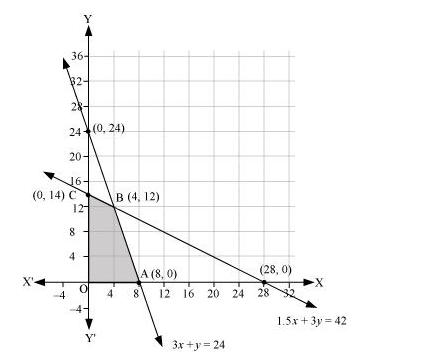
The corner points are A (8, 0), B (4, 12), C (0, 14), and O (0, 0).
The values of Z at these corner points are as follows.
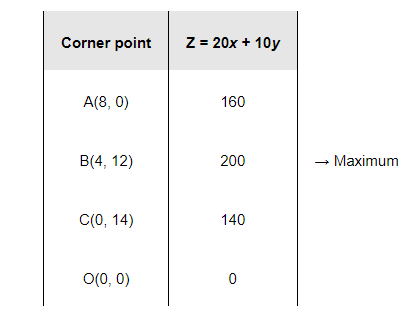
Thus, the maximum profit of the factory when it works to its full capacity is Rs 200.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
