A field is in the shape of a trapezium having parallel sides 90 m and 30 m.

In the given figure, ABCD is a trapezium having parallel sides 90 m and 30 m.

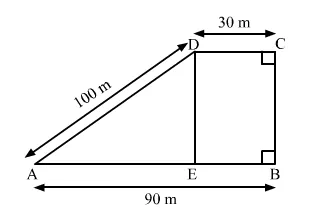
Draw DE perpendicular to AB, such that DE = BC.

In right angled ∆ADE,

$A D^{2}=A E^{2}+E D^{2}$         (Pythagoras Theorem)

$\Rightarrow 100^{2}=(90-30)^{2}+E D^{2}$

$\Rightarrow 10000=3600+E D^{2}$

$\Rightarrow E D^{2}=10000-3600$

$\Rightarrow E D^{2}=6400$

$\Rightarrow E D=80 \mathrm{~m}$

Thus, the height of the trapezium = 80 m        ...(1)

Now,

Area of trapezium $=\frac{1}{2} \times$ sum of parallel sides $\times$ height

$=\frac{1}{2} \times(90+30) \times 80$

$=4800 \mathrm{~m}^{2}$

The cost to plough per $\mathrm{m}^{2}=$ Rs 5

The cost to plough $4800 \mathrm{~m}^{2}=$ Rs $5 \times 4800$

 = Rs 24000

Hence, the total cost of ploughing the field is Rs 24000.