A girl of heigh 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/sec.

It is given that, girl height $=90 \mathrm{~cm}$, speed $=1.2 \mathrm{~m} / \mathrm{sec}$ and height of lamp $=3.6 \mathrm{~m}$.

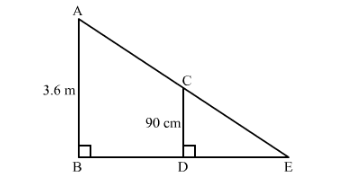
We have to find the length of her shadow after $4 \mathrm{sec}$

Let $A B$ be the lamp post and $C D$ be the girl.

Suppose $D E$ is the length of her shadow.

Let $D E=x$

And 

$B D=1.2 \times 4$

$=4.8 \mathrm{~m}$

Now in $\triangle A B E$ and $\triangle C D E$ we have

$\angle B=\angle D$ and $\angle E=\angle E$

So by $A A$ similarly criterion $\triangle A B E \sim \triangle C D E$

$\mathrm{BEDE}=\mathrm{ABCD} 4.8+\mathrm{XX}=3.60 .9=4 \Rightarrow 3 \mathrm{x}=4.8 \Rightarrow \mathrm{x}=1.6$

Hence the length of her shadow after $4 \sec$ is $1.6 \mathrm{~m}$.