A hemisphere and a cone have equal bases.

Solution:

The base of the cone and hemisphere are equal. So radius of the two is also equal.

and

Height of the hemisphere = height of the cone

Then the slant height of the cone

$I=\sqrt{r^{2}+h^{2}}$

$=\sqrt{r^{2}+r^{2}}$

$=\sqrt{2 r^{2}}$

 

$=r \sqrt{2}$  ............(i)

Now, the curved surface area of

Hemisphere $=2 \pi r^{2}$

and

The curved surface area of cone 

Putting the value of l from eq. (i)

We get

$=\pi r \sqrt{2} r$

$=\pi r^{2} \sqrt{2} r$

Now,

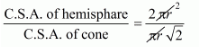
$=\frac{2}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}$

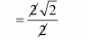
$=\sqrt{2}: 1$