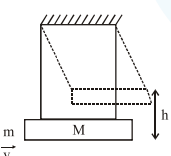
A large block of wood of mass $\mathrm{M}=5.99 \mathrm{~kg}$ is hanging from two long massless cords. A bullet of mass $m=10 \mathrm{~g}$ is fired into the block and gets embedded in it. The (block + bullet) then swing upwards, their centre of mass rising a vertical distance $\mathrm{h}=9.8 \mathrm{~cm}$ before the (block + bullet) pendulum comes momentarily to rest at the end of its arc. The speed of the bullet just before collision is : (Take $\mathrm{g}=9.8 \mathrm{~ms}^{-2}$ )
Correct Option: , 3
From energy conservation,
$\left[\begin{array}{l}\text { after bullet gets embedded till the } \\ \text { system comes momentarily at rest }\end{array}\right]$
$(\mathrm{M}+\mathrm{m}) \mathrm{g} h=\frac{1}{2}(\mathrm{M}+\mathrm{m}) \mathrm{v}_{1}^{2}$
[ $\mathrm{v}_{1}$ is velocity after collision]
$\therefore v_{1}=\sqrt{2 g h}$
Applying momentum conservation, (just before and just after collision)
$\mathrm{mv}=(\mathrm{M}+\mathrm{m}) \mathrm{v}_{1}$
$v=\left(\frac{\mathrm{M}+\mathrm{m}}{\mathrm{m}}\right) \mathrm{v}_{1}=\frac{6}{10 \times 10^{-3}} \times \sqrt{2 \times 9.8 \times 9.8 \times 10^{-2}}$
$\approx 831.55 \mathrm{~m} / \mathrm{s}$
