A light ray enters a solid glass sphere of refractive index

$(\mathbf{9 0 . 0 0})$

In the figure, $Q R$ is the reflected ray and $Q S$ is refracted ray. $C Q$ is normal.

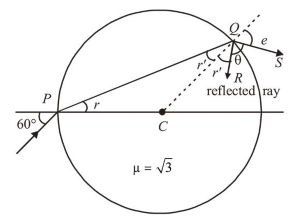
Apply Snell's law at $P$

$1 \sin 60^{\circ}=\sqrt{3} \sin r$

$\Rightarrow \sin r=\frac{1}{2} \Rightarrow r=30^{\circ}$

From geometry, $C P=C Q$

$\therefore r^{\prime}=30^{\circ}$

Again apply snell's law at $Q$,

$\sqrt{3} \sin r^{\prime}=1 \sin e$

$\Rightarrow \frac{\sqrt{3}}{2}=\sin e \Rightarrow e=60^{\circ}$

From geometry

$r^{\prime}+\theta+e=180^{\circ} \quad$ (As angles lies on a straight line)

$\Rightarrow 30^{\circ}+\theta+60^{\circ}=180^{\circ} \Rightarrow \theta=90^{\circ}$