A man goes 10 m due south and then 24 due west.

Let the man starts from point D and goes 10 m due south and stops at E. He then goes 24 m due west at F.

In right $\triangle \mathrm{DEF}$, we have:

DE = 10 m, EF = 24 m

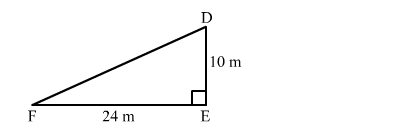
$D F^{2}=E F^{2}+D E^{2}$

$D F=\sqrt{10^{2}+24^{2}}$

$=\sqrt{100+576}$

$=\sqrt{676}$

$=26 \mathrm{~m}$

Hence, the man is 26 m away from the starting point.