A metre stick is balanced on a knife edge at its centre.

Let W and W′ be the respective weights of the metre stick and the coin.

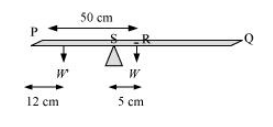
The mass of the metre stick is concentrated at its mid-point, i.e., at the 50 cm mark.

Mass of the meter stick $=m^{\prime}$

Mass of each coin, m = 5 g

When the coins are placed 12 cm away from the end P, the centre of mass gets shifted by 5 cm from point R toward the end P. The centre of mass is located at a distance of 45 cm from point P.

The net torque will be conserved for rotational equilibrium about point R.

$10 \times g(45-12)-m^{\prime} g(50-45)=0$

$\therefore m^{\prime}=\frac{10 \times 33}{5}=66 \mathrm{~g}$

Hence, the mass of the metre stick is $66 \mathrm{~g}$.