A point like object is placed at a distance of 1 m

(4) Focal length of the convex lens, $f=0.5 \mathrm{~m}$

Object is at $2 f$ so, image $\left(I_{1}\right)$ will also be at $2 f$.

Image of $I_{1}$ i.e., $I_{2}$ will be $1 \mathrm{~m}$ behind mirror.

Now $I_{2}$ will be object for lens.

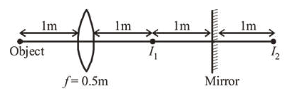
$\therefore u=(-1)+(-1)+(-1)=-3 \mathrm{~m}$

Using lens formula, $\frac{1}{v}-\frac{1}{u}=\frac{1}{f}$

$\frac{1}{v}=\frac{1}{f}+\frac{1}{u}=\frac{1}{+0.5}+\frac{1}{-3}$ or $v=\frac{3}{5}=0.6 \mathrm{~m}$

Hence, distance of image from mirror

$=2+0.6=2.6 \mathrm{~m}$ and real.