Question:
A pole stands vertically inside a triangular park ABC. Let the angle of elevation of the top of the pole from each corner of the park be $\frac{\pi}{3}$. If the radius of the circumcircle ot $\triangle \mathrm{ABC}$ is 2 , then the height of the pole is equal to:
Correct Option: , 2
Solution:
Let $\mathrm{PD}=\mathrm{h}, \mathrm{R}=2$
As angle of elevation of top of pole from $A, B, C$ are equal So $\mathrm{D}$ must be circumcentre of $\Delta \mathrm{ABC}$
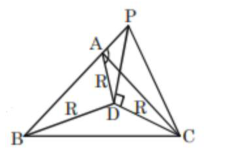
$\tan \left(\frac{\pi}{3}\right)=\frac{\mathrm{PD}}{\mathrm{R}}=\frac{\mathrm{h}}{\mathrm{R}}$
$\mathrm{h}=\mathrm{R} \tan \left(\frac{\pi}{3}\right)=2 \sqrt{3}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.