Question.
A right triangle $A B C$ with sides $5 \mathrm{~cm}, 12 \mathrm{~cm}$ and $13 \mathrm{~cm}$ is revolved about the side $12 \mathrm{~cm}$. Find the volume of the solid so obtained.
A right triangle $A B C$ with sides $5 \mathrm{~cm}, 12 \mathrm{~cm}$ and $13 \mathrm{~cm}$ is revolved about the side $12 \mathrm{~cm}$. Find the volume of the solid so obtained.
Solution:
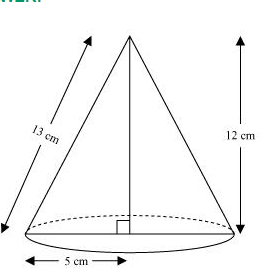
When right-angled $\triangle \mathrm{ABC}$ is revolved about its side $12 \mathrm{~cm}$, a cone with height $(h)$ as $12 \mathrm{~cm}$, radius $(r)$ as $5 \mathrm{~cm}$, and slant height $(l) 13 \mathrm{~cm}$ will be formed.
Volume of cone $=\frac{1}{3} \pi r^{2} h$
$=\left[\frac{1}{3} \times \pi \times(5)^{2} \times 12\right] \mathrm{cm}^{3}$
$=100 \pi \mathrm{cm}^{3}$
Therefore, the volume of the cone so formed is $100 \pi \mathrm{cm}^{3}$.

When right-angled $\triangle \mathrm{ABC}$ is revolved about its side $12 \mathrm{~cm}$, a cone with height $(h)$ as $12 \mathrm{~cm}$, radius $(r)$ as $5 \mathrm{~cm}$, and slant height $(l) 13 \mathrm{~cm}$ will be formed.
Volume of cone $=\frac{1}{3} \pi r^{2} h$
$=\left[\frac{1}{3} \times \pi \times(5)^{2} \times 12\right] \mathrm{cm}^{3}$
$=100 \pi \mathrm{cm}^{3}$
Therefore, the volume of the cone so formed is $100 \pi \mathrm{cm}^{3}$.
