A rocket is fired from the earth towards the sun.

Mass of the Sun, $M_{s}=2 \times 10^{30} \mathrm{~kg}$

Mass of the Earth, $M_{\mathrm{e}}=6 \times 10^{24} \mathrm{~kg}$

Orbital radius, $r=1.5 \times 10^{11} \mathrm{~m}$

Mass of the rocket $=m$

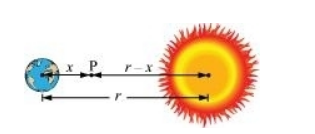
Let x be the distance from the centre of the Earth where the gravitational force acting on satellite P becomes zero.

From Newton’s law of gravitation, we can equate gravitational forces acting on satellite P under the influence of the Sun and the Earth as:

$\frac{\mathrm{G} m M_{s}}{(r-x)^{2}}=\mathrm{G} m \frac{M_{e}}{x^{2}}$

$\left(\frac{r-x}{x}\right)^{2}=\frac{M_{s}}{M_{e}}$

$\frac{r-x}{x}=\left(\frac{2 \times 10^{30}}{60 \times 10^{24}}\right)^{\frac{1}{2}}=577.35$

$1.5 \times 10^{11}-x=577.35 x$

$578.35 x=1.5 \times 10^{11}$

$x=\frac{1.5 \times 10^{11}}{578.35}=2.59 \times 10^{8} \mathrm{~m}$