Question.
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative]
A stone of mass m tied to the end of a string revolves in a vertical circle of radius R. The net forces at the lowest and highest points of the circle directed vertically downwards are: [Choose the correct alternative]
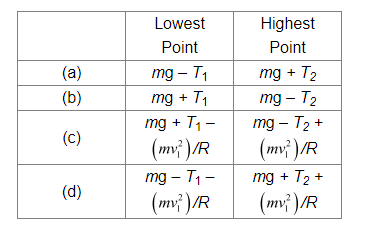
$T_{1}$ and $v_{1}$ denote the tension and speed at the lowest point. $T_{2}$ and $v_{2}$ denote corresponding values at the highest point.
solution:
(a)The free body diagram of the stone at the lowest point is shown in the following figure.
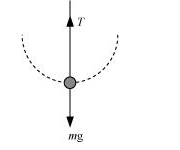
According to Newton’s second law of motion, the net force acting on the stone at this point is equal to the centripetal force, i.e.,
$F_{\text {tet }}=T-m \mathrm{~g}=\frac{m v_{1}^{2}}{R} \ldots(i)$
Where, $v_{1}=$ Velocity at the lowest point
The free body diagram of the stone at the highest point is shown in the following figure.
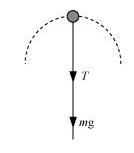
Using Newton’s second law of motion, we have:
$T+m g=\frac{m v_{2}^{2}}{R} \ldots$
Where, $v_{2}=$ Velocity at the highest point
It is clear from equations $(i)$ and $(i i)$ that the net force acting at the lowest and the highest points are respectively $(T-m g)$ and $(T+m g)$.
(a)The free body diagram of the stone at the lowest point is shown in the following figure.

According to Newton’s second law of motion, the net force acting on the stone at this point is equal to the centripetal force, i.e.,
$F_{\text {tet }}=T-m \mathrm{~g}=\frac{m v_{1}^{2}}{R} \ldots(i)$
Where, $v_{1}=$ Velocity at the lowest point
The free body diagram of the stone at the highest point is shown in the following figure.

Using Newton’s second law of motion, we have:
$T+m g=\frac{m v_{2}^{2}}{R} \ldots$
Where, $v_{2}=$ Velocity at the highest point
It is clear from equations $(i)$ and $(i i)$ that the net force acting at the lowest and the highest points are respectively $(T-m g)$ and $(T+m g)$.
