Question:
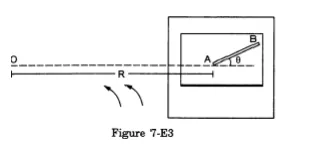
A table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity co in a circular path of radius $\mathrm{R}$ (figure 7-E3). A smooth groove $\mathrm{AB}$ of length $\mathrm{L}(\ll \mathrm{R}$ ) is made on the surface of the table. The groove makes an angle 0 with the radius $\mathrm{OA}$ of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along $A B$. Find the time taken by the particle to reach the point $B$.
Solution:

