A takes 10 days less than the time taken by B to finish a piece of work.

Let $B$ alone takes $x$ days to finish the work. Then, $B$ 's one day's work $=\frac{1}{x}$.

Similarly, $A$ alone can finish it in $(x-10)$ days to finish the work. Then, $A$ 's one day's work $=\frac{1}{x-10}$.

It is given that

A's one day's work $+B$ 's one day's work $=(A+B)$ 's one day's work

$\frac{1}{x}+\frac{1}{x-10}=\frac{1}{12}$

$\frac{x-10+x}{x(x-10)}=\frac{1}{12}$

$\frac{2 x-10}{x(x-10)}=\frac{1}{12}$

$x^{2}-10 x=24 x-120$

$x^{2}-10 x-24 x+120=0$

$x^{2}-34 x+120=0$

$x^{2}-30 x-4 x+120=0$

$x(x-30)-4(x-30)=0$

$(x-30)(x-4)=0$

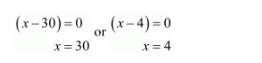
But $x=3$ is not correct.

therefore, $x=30$ is correct

Hence, the time taken by $B$ to finish the work in $x=30$ days