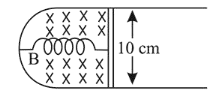
A thin strip $10 \mathrm{~cm}$ long is on a $U$ shaped wire of negligible resistance and it is connected to a spring of spring constant $0.5 \mathrm{Nm}^{-1}$ (see figure). The assembly is kept in a uniform magnetic field of $0.1 \mathrm{~T}$. If the strip is pulled from its equilibrium position and released, the number of oscillations it performs before its amplitude decreases by a factor of $e$ is $\mathrm{N}$. If the mass of strip is 50 grams, its resistance $10 \Omega$ and air drag negligible, $N$ will be close to :
Correct Option: , 3
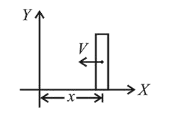
(3) Force on the strip when it is at stretched position $x$ from mean position is
$F=-k x-i I B=-k x-\frac{B I v}{R} \times I B$
$F=-k x-\frac{B^{2} I^{2}}{R} \times v$
Above expression shows that it is case of damped oscillation, so its amplitude can be given by
$\Rightarrow A=A_{0} e^{-\frac{b t}{2 m}}$
$\Rightarrow \frac{A_{0}}{e}=A_{0} e^{-\frac{b t}{2 m}}\left[\right.$ as per question $\left.A=\frac{A_{0}}{e}\right]$
$\Rightarrow t=\frac{2 m}{\left(\frac{B^{2} I^{2}}{R}\right)}=\frac{2 \times 50 \times 10^{-3} \times 10}{0.01 \times 0.01}$
$=10000 \mathrm{~s}$
Given, $m=50 \times 10^{-3} \mathrm{~kg}$
$\mathrm{B}=0.1 \mathrm{~T}$
$l=0.1 \mathrm{~m}$
$\mathrm{R}=10 \Omega$
$\mathrm{k}=0.5 \mathrm{~N}$
Time period, $T=2 \pi \sqrt{\frac{m}{k}} \simeq 2 \mathrm{~s}$
so, required number of oscillations,
$N=\frac{10000}{2}=5000$
