Question:
A tower stand vertically on the ground. From a point on the ground 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower?
Solution:
Let 
be the tower of height 
m and C be the point on the ground, makes an angle of elevation 
with the top of tower.
In a triangle
, given that BC = 20 m and 
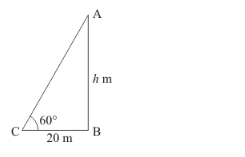
Now we have to find height of tower, so we use trigonometrical ratios.
In the triangle,
$\Rightarrow \tan C=\frac{A B}{B C}$
$\Rightarrow \sqrt{3}=\frac{h}{20}$
$\Rightarrow h=20 \sqrt{3}$
Hence height of tower is $20 \sqrt{3}$ meters.