A uniform thin bar of mass $6 \mathrm{~kg}$ and length $2.4$ meter is bent to make an equilateral hexagon. The moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of hexagon is $\times 10^{-1} \mathrm{~kg} \mathrm{~m}^{2}$
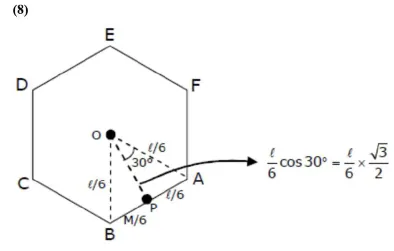
MOI of $\mathrm{AB}$ about $P: I_{A B_{p}}=\frac{\frac{M}{6}\left(\frac{1}{6}\right)^{2}}{12}$
MOI of $A B$ about $O, I_{A B_{0}}=\left[\frac{\frac{M}{6}\left(\frac{\ell}{6}\right)^{2}}{12}+\frac{M}{6}\left(\frac{\ell}{6} \frac{\sqrt{3}}{2}\right)^{2}\right]$
$\mathrm{I}_{\mathrm{Hexagon}_{0}}=6 \mathrm{I}_{\mathrm{AB}_{0}}=\mathrm{M}\left[\frac{\ell^{2}}{12 \times 36}+\frac{\ell^{2}}{36} \times \frac{3}{4}\right]$
$=\frac{6}{100}\left[\frac{24 \times 24}{12 \times 36}+\frac{24 \times 24}{36} \times \frac{3}{4}\right]$
$=0.8 \mathrm{kgm}^{2}$
$=8 \times 10^{-2} \mathrm{~kg} / \mathrm{m}^{2}$
