Question:
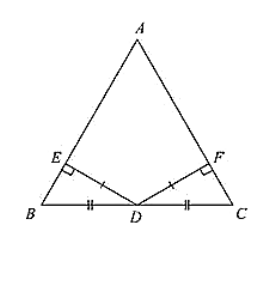
ABC is a triangle and D is the mid-point of BC. The perpendiculars from B to AB and AC are equal. Prove that the triangle is isosceles.
Solution:
Given that, in two right triangles one side and acute angle of one are equal to the corresponding side and angle of the other
We have to prove that the triangles are congruent
Let us consider two right triangles such that
∠B = ∠E = 90 ... (i)
AB = DE ... (ii)
∠C = ∠F ... (iii)
Now observe the two triangles ABC and DEF
∠C = ∠F [From (iii)]
∠B = ∠E [From (i)]
And AB = DE [From (ii)]
So, by AAS congruence criterion, we have
ΔABC ≅ ΔDEF
Therefore, the two triangles are congruent
Hence proved
