Question:
ABC is a triangle in which ∠A = 720°, the internal bisectors of angles B and C meet in O. Find the magnitude of ∠BOC.
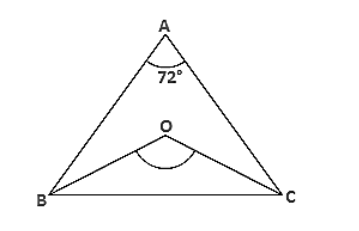
Solution:
Given,
ABC is a triangle where ∠A = 72° and the internal bisector of angles B and C meeting O.
In ΔABC,
∠A + ∠B + ∠C = 180°
⇒ 72° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 180° − 72°
Dividing both sides by '2'
⇒ ∠B/2 + ∠C/2 = 108°/2
⇒ ∠OBC + ∠OCB = 54°
Now, In ΔBOC ⇒ ∠OBC + ∠OCB + ∠BOC = 180°
⇒ 540° + ∠BOC = 180°
⇒ ∠BOC = 180° − 54°=126°
∴ ∠BOC = 126°
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.