ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D.

Question:
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = 1/2∠A.

Solution:

Let ∠ABE = 2x and ∠ACB = 2y

∠ABC = 180° − 2x [Linear pair]

∴ ∠A = 180° − ∠ABC − ∠ACB [Angle sum property]

= 180° − 180° + 2x + 2y

= 2(x − y) ..... (i)

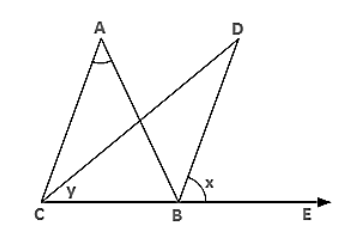
Now, ∠D = 180° − ∠DBC − ∠DCB

⇒ ∠D = 180° − (x + 180° − 2x) − y

⇒ ∠D = 180° − x − 180° + 2x − y

= (x − y)

$=\frac{1}{2} \angle \mathrm{A} \ldots .$ from(i)

Hence, $\angle \mathrm{D}=\frac{1}{2} \angle \mathrm{A}$.