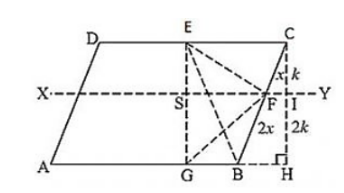
ABCD is a parallelogram. G is a point on AB such that AG = 2GB and E is point

Given: ABCD is a parallelogram

AG = 2 GB, CE = 2 DE and BF = 2 FC

To prove:

(i) ar(ADEG) = ar(GBCE).

(ii) ar(ΔEGB) = (1/6) ar(ABCD).

(iii) ar(ΔEFC) = (1/2) ar(ΔEBF).

(iv) ar(ΔEGB) = (3/2) × ar(ΔEFC)

(v) Find what portion of the area of parallelogram is the area of ΔEFG.

Construction: Draw a parallel line to AB through point F and a perpendicular line to AB from C

Proof:

(i) Since ABCD is a parallelogram

So, AB = CD and AD = BC

Consider the two trapezium s ADEG and GBCE

Since AB = DC, EC = 2DE, AG = 2GB

⇒ ED = (1/3) CD = (1/3) AB and EC = (2/3) CD = (2/3) AB

⇒ AG = (2/3) AB and BG = (1/3) AB

So, DE + AG = (1/3) AB + (2/3) AB = AB and EC + BG = (2/3) AB + (1/3) AB = AB

Since the two trapezium ADEG and GBCE have same height and their sum of two parallel sides are equal

Since

Area of trapezium $=\frac{\text { Sum of parallel sides }}{2} \times$ height

So, ar(ADEG) = ar(GBCE).

(ii) Since we know from above that

BG = (1/2) AB So

ar(ΔEGB) = (1/2) × GB × Height

ar(ΔEGB) = (1/2) × (1/3) × AB × Height

ar(ΔEGB) = (1/6) × AB × Height

ar(ΔEGB) = (1/6) ar(ABCD).

(iii) Since height if triangle EFC and EBF are equal. So

ar(ΔEFC) = (1/2) × FC × Height

ar(ΔEFC) = (1/2) × (1/2) × FB × Height

ar(ΔEFC) = (1/2) ar(EBF)

Hence, ar(ΔEFC) = (1/2) ar(ΔEBF).

(iv) Consider the trapezium in which

ar(EGBC) = ar(ΔEGB) + ar(ΔEBF) + ar(ΔEFC)

⇒ (1/2) ar(ABCD) = (1/6) ar(ABCD) + 2ar(ΔEFC) + ar(ΔEFC)

⇒ (1/3) ar(ABCD) = 3 ar(ΔEFC)

⇒ ar(ΔEFC) = (1/9) ar(ABCD)

Now from (ii) part we have

ar(ΔEGB) = (1/6) ar(ΔEFC)

ar(ΔEGB) = (3/2) × (1/9) ar(ABCD)

ar(ΔEGB) = (3/2) ar(ΔEFC)

∴ ar(ΔEGB) = (3/2) ar(ΔEFC)

(v) In the figure it is given that FB = 2CF.

Let CF = x and FB = 2x.

Now consider the two triangles CFI and CBH which are similar triangle.

So by the property of similar triangle CI = k and IH = 2k

Now consider the triangle EGF in which

ar(ΔEFG) = ar(ΔESF) + ar(ΔSGF)

ar(ΔEFG) = (1/2) SF × k + (1/2) SF × 2k

ar(ΔEFG) = (3/2) SF × k   ⋅⋅⋅ (i)

Now,

ar(ΔEGBC) = ar(SGBF) + ar(ESFC)

ar(ΔEGBC) = (1/2)(SF + GB) × 2k + (1/2)(SF + EC) × k

ar(ΔEGBC) = (3/2) k × SF + (GB + (1/2)EC) × k

ar(ΔEGBC) = (3/2) k × SF + (1/3 AB + (1/2) × (2/3) AB) × k

(1/2) ar(ΔABCD) = (3/2) k × SF + (2/3) AB × k

⇒ ar(ΔABCD) = 3k × SF + (4/3) AB × k       [Multiply both sides by 2]

⇒ ar(ΔABCD) = 3k × SF + 4/9 ar(ABCD)

⇒ k × SF = (5/27 )ar(ABCD) ⋅⋅⋅⋅  (2)

From 1 and 2 we have,

ar(ΔEFG) = (3/2) × (5/27) ar(ABCD)

ar(ΔEFG) = (5/18) ar(ABCD)