Question.
Aftab tells his daughter, "Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be". (Isn't this interesting?) Represent this situation algebraically and graphically.
Aftab tells his daughter, "Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be". (Isn't this interesting?) Represent this situation algebraically and graphically.
Solution:
Let the present age of Aftab's daughter = x years.
and the present age of $A f t a b=y$ years $(y>x)$
According to the given conditions
Seven years ago,
$(y-7)=7 \times(x-7)$
i.e., $\quad y-7=7 x-49$
i.e., $\quad 7 x-y-42=0$...(1)
Three years later, $(y+3)=3 \times(x+3)$
i.e., $\quad y+3=3 x+9$
i.e., $\quad 3 x-y+6=0$ ...(2)
Thus, the algebraic relations are $7 x-y-42=0,3 x-y+6=0$.
Now, we represent the problem graphically as below : $7 x-y-42=0$ ...(1)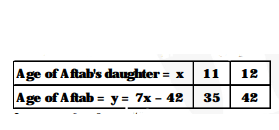
$3 x-y+6=0 \quad$...(ii)

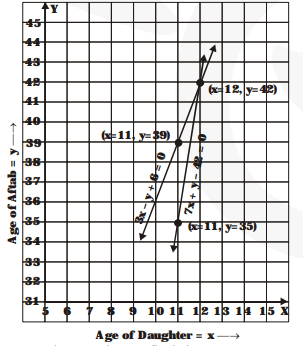
From the graph, we find that
x = 12
and y = 42
Thus, the present age of Aftab's daugther = 12 years
and the present age of Aftab = 42 years
Let the present age of Aftab's daughter = x years.
and the present age of $A f t a b=y$ years $(y>x)$
According to the given conditions
Seven years ago,
$(y-7)=7 \times(x-7)$
i.e., $\quad y-7=7 x-49$
i.e., $\quad 7 x-y-42=0$...(1)
Three years later, $(y+3)=3 \times(x+3)$
i.e., $\quad y+3=3 x+9$
i.e., $\quad 3 x-y+6=0$ ...(2)
Thus, the algebraic relations are $7 x-y-42=0,3 x-y+6=0$.
Now, we represent the problem graphically as below : $7 x-y-42=0$ ...(1)
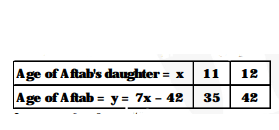
$3 x-y+6=0 \quad$...(ii)


From the graph, we find that
x = 12
and y = 42
Thus, the present age of Aftab's daugther = 12 years
and the present age of Aftab = 42 years
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
