An amplitude modulated signal is given by

$v(t)=10\left\lfloor 1+u .5 \cos \left(2.2 \times 10^{\top}\right)\right\rfloor$

$\sin \left(5.5 \times 10^{5} t\right)$

$=10+1.5\left[\sin \left(57.2 \times 10^{4} \mathrm{t}\right)+\sin \left(52.8 \times 10^{4} \mathrm{t}\right)\right]$

$\omega_{\mathrm{c}}+\omega_{\mathrm{w}}=57.2 \times 10^{4}=2 \pi \mathrm{f}_{1}$

$\mathrm{f}_{1}=\frac{57.2 \times 10^{4}}{2 \times\left(\frac{22}{7}\right)}=9.1 \times 10^{4} \simeq 91 \mathrm{KHz}$

$\omega_{\mathrm{c}}-\omega_{\mathrm{w}}=52.8 \times 10^{4}$

$\mathrm{f}_{2}=\frac{52.8 \times 10^{4}}{2 \times\left(\frac{22}{7}\right)}=84 \mathrm{KHz}$

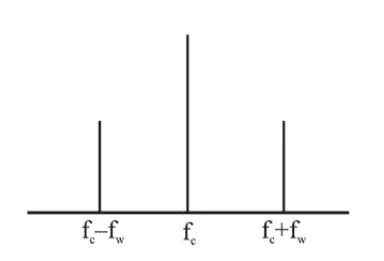
Upper side band frequency $\left(f_{1}\right)$ is

$\mathrm{f}_{1}=\mathrm{f}_{\mathrm{c}}-\mathrm{f}_{\mathrm{w}}=\frac{52.8 \times 10^{4}}{2 \pi} \approx 85.00 \mathrm{kHz}$

Lower side band frequency $\left(f_{2}\right)$ is

$\mathrm{f}_{2}=\mathrm{f}_{\mathrm{c}}+\mathrm{f}_{\mathrm{w}}=\frac{57.2 \times 10^{4}}{2 \pi} \approx 90.00 \mathrm{kHz}$