An amplitude modulated signal is plotted below:

Question:

An amplitude modulated signal is plotted below:

Which one of the following best describes the above signal?

  1. (1) $\left(9+\sin \left(2.5 \pi \times 10^{5} \mathrm{t}\right)\right) \sin \left(2 \pi \times 10^{4} \mathrm{t}\right) \mathrm{V}$

  2. (2) $\left(1+9 \sin \left(2 \pi \times 10^{4} \mathrm{t}\right)\right) \sin \left(2.5 \pi \times 10^{5} \mathrm{t}\right) \mathrm{V}$

  3. (3) $\left(9+\sin \left(2 \pi \times 10^{4} \mathrm{t}\right)\right) \sin \left(2.5 \pi \times 10^{5} \mathrm{t}\right) \mathrm{V}$

  4. (4) $\left(9+\sin \left(4 \pi \times 10^{4} \mathrm{t}\right)\right) \sin \left(5 \pi \times 10^{5} \mathrm{t}\right) \mathrm{V}$

Correct Option: , 3

Solution:

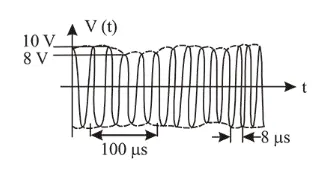
(3) After analysing the graph we may conclude that

(i) Amplitude varies as $8-10 \mathrm{~V}$ or $9 \pm 1$

(ii) Two time period as

$100 \mu \mathrm{s}$ (signal wave) \& $8 \mu \mathrm{s}$ (carrier wave)

So, equation of AM signal is

$\left[9 \pm 1 \sin \left(\frac{2 \pi t}{T_{1}}\right) \sin \left(\frac{2 \pi t}{T_{2}}\right)\right]$

$\left.=\left[9 \pm \sin \left(2 \pi \times 10^{4} \mathrm{t}\right)\right] \sin \left(2.5 \pi \times 10^{5} \mathrm{t}\right) \mathrm{V}\right]$

Leave a comment

eSaral Gurukul

NEET

JEE Main

JEE Advanced

Our Telegram Channel

All Study Material