An ice-cream cone full of ice-cream having radius 5 cm and height 10 cm as shown in figure
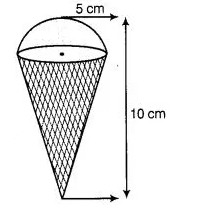
Calculate the volume of ice-cream, provided that its $\frac{1}{6}$ part is left unfilled with ice-cream.
Given, ice-cream cone is the combination of a hemisphere and a cone.
Also , radius of hemisphere = 5 cm
$\therefore \quad$ Volume of hemisphere $=\frac{2}{3} \pi r^{3}=\frac{2}{3} \times \frac{22}{7} \times(5)^{3}$
$=\frac{5500}{21}=261.90 \mathrm{~cm}^{3}$
Now, radius of the cone $=5 \mathrm{~cm}$
and $\quad$ height of the cone $=10-5=5 \mathrm{~cm}$
$\therefore \quad$ Volume of the cone $=\frac{1}{3} \pi r^{2} h$
$=\frac{1}{3} \times \frac{22}{7} \times(5)^{2} \times 5$
$=\frac{2750}{21}=130.95 \mathrm{~cm}^{3}$
Now, total volume of ice-cream cone $=261.90+130.95=392.85 \mathrm{~cm}^{3}$ Since, $\frac{1}{6}$ part is left unfilled with ice-cream.
$\therefore$ Required volume of ice-cream $=392.85-392.85 \times \frac{1}{6}=392.85-65.475$
$=327.4 \mathrm{~cm}^{3}$
