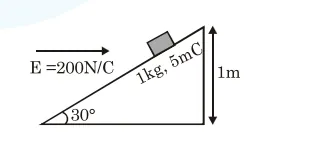
An inclined plane making an angle of

Question:

An inclined plane making an angle of $30^{\circ}$ with the horizontal is placed in a uniform horizontal

electric field $200 \frac{\mathrm{N}}{\mathrm{C}}$ as shown in the figure. A body

of mass $1 \mathrm{~kg}$ and charge $5 \mathrm{mC}$ is allowed to slide down from rest at a height of $1 \mathrm{~m}$. If the coefficient of friction is $0.2$, find the time taken by the body

to reach the bottom. $\left[g=9.8 \mathrm{~m} / \mathrm{s}^{2}, \sin 30^{\circ}=\frac{1}{2}\right.$

$\left.\cos 30^{\circ}=\frac{\sqrt{3}}{2}\right]$

  1. $0.92 \mathrm{~s}$

  2. $0.46 \mathrm{~s}$

  3. $2.3 \mathrm{~s}$

  4. $1.3 \mathrm{~s}$

Correct Option: , 4

Solution:

FBD

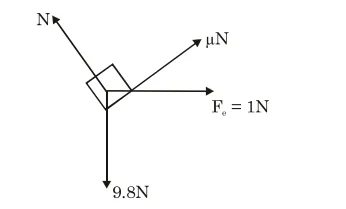
here $\mathrm{N}=9.8 \cos 30+1 \sin 30$ $\approx 9 \mathrm{~N}$

so $\mathrm{a}=\frac{9.8 \sin 30-1 \cos 30-\mu \mathrm{N}}{1}$

$\mathrm{a}=2.233 \mathrm{~m} / \mathrm{s}^{2}$

By $S=u t+\frac{1}{2} a t^{2}$

$=\frac{1}{2}(2.233) \mathrm{t}^{2}$

$\sin 30^{\circ}$

$\mathrm{t} \approx 1.3 \mathrm{sec}$

 

Leave a comment

None

All Study Material

Free Study Material