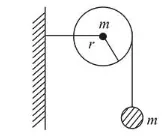
As shown in the figure, a bob of mass $m$ is tied by a massless string whose other end portion is wound on a fly wheel (disc) of radius $\mathrm{r}$ and mass $\mathrm{m}$. When released from rest the bob starts falling vertically. When it has covered a distance of $\mathrm{h}$, the angular speed of the wheel will be:
Correct Option: 1
(1) When the bob covered a distance ' $h$ '
Using $m g h=\frac{1}{2} m v^{2}+\frac{1}{2} I \omega^{2}$
$=\frac{1}{2} \mathrm{~m}(\omega \mathrm{r})^{2}+\frac{1}{2} \times \frac{m r^{2}}{2} \times \omega^{2}(\because v=\omega r$ no slipping $)$
$\Rightarrow \quad m g h=\frac{3}{4} m \omega^{2} r^{2}$
$\Rightarrow \omega=\sqrt{\frac{4 g h}{3 r^{2}}}=\frac{1}{r} \sqrt{\frac{4 g h}{3}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.