Construct a $\triangle A B C$, in which $B C=6.5 \mathrm{~cm}, A B=4.5 \mathrm{~cm}$ and $\angle A B C=60^{\circ}$. Construct a triangle similar to this triangle whose sides are $\frac{3}{4}$ the corresponding sides of $\triangle A B C$.
Steps of Construction :
Step 1. Draw a line segment BC = 6.5 cm.
Step 2. With B as centre, draw an angle of 60o.
Step 3. With B as centre and radius equal to 4.5 cm, draw an arc, cutting the angle at A.
Step 4. Join AB and AC.
Thus, △ ABC is obtained .
Step 5. Below $B C$, draw an acute $\angle C B X$.
Step 6. Along BX, mark off four points B1, B2, B3, B4, such that BB1 = B1B2 = B2B3 = B3B4 .
Step 7. Join B4C.
Step 8. From B3, draw B3D ∥ B4C, meeting BC at D.
Step 9. From D, draw DE ∥ CA, meeting AB at E.
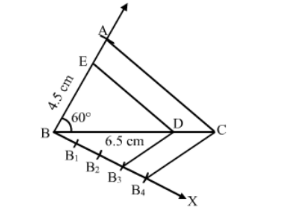
Thus, $\triangle \mathrm{EBD}$ is the required triangle, each of whose sides is $\frac{3}{4}$ the corresponding sides of $\triangle A B C$.
