Construct a $\triangle A B C$ with $B C=6 \mathrm{~cm}, \angle B=60^{\circ}$ and $A B=5 \mathrm{~cm}$. Construct another triangle whose sides are $\frac{3}{4}$ times the corresponding sides of $\triangle A B C$.
Given: In ΔABC,
BC = 6 cm,
∠B = 60°
AB = 5 cm
Steps of construction:
(1) Draw a line segment AB = 5 cm.
(2) From the point B, draw an ∠ABY = 60°
(3) Taking B as center, 6 cm radius, draw an arc on the ray BY,
Let the point where the arc intersects the ray named as C.
(4) Join AC.
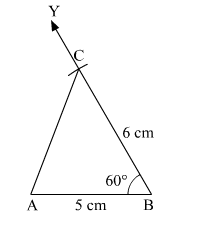
Hence, ΔABC is the required triangle.
Now, we construct another triangle whose sides are $\frac{3}{4}$ times the corresponding sides of $\triangle A B C$.
Steps of construction:
(1) Draw any ray BX making an acute angle with BA on the side opposite to the vertex C.
(2) Mark four points B1, B2, B3 and B4 on BX, so that BB1 = B1B2 = B2B3 = B3B4.
(3) Join B4A and draw a line through B3 parallel to B4A to intersect AB at A'.
(4) Draw a line through A' parallel to AC to intersect BC at C'.
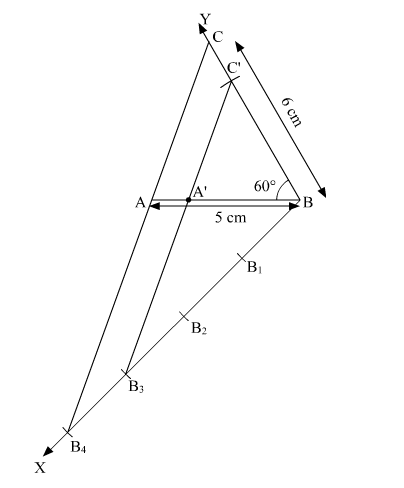
Hence, ΔA'BC' is the required triangle.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.