D is the mid-point of side BC of a ∆ABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE = EX = 3 : 1
Given: ABC is a triangle in which D is the mid point of BC, E is the mid point of AD. BE produced meets AC at X.
To Prove: BE : EX = 3:1.
Construction: We draw a line DY parallel to BX.
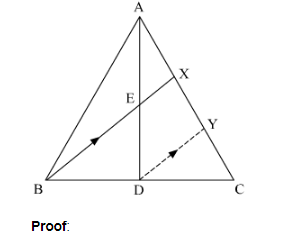
In $\triangle \mathrm{BCX}$ and $\triangle \mathrm{DCY}, \angle \mathrm{CBX}=\angle \mathrm{CDY}$ Corresponding angles $\angle \mathrm{CXB}=\angle \mathrm{CYD}$ Corresponding angles $\triangle \mathrm{BCX} \sim \triangle \mathrm{DCY}$ AA similarityWe know that corresponding sides of similar triangles are proportional. Thus, BCD
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
